我們討論了電感元件的串并聯的計算，今天我們進行深入學習探討互感電感的串并聯計算問題，那互感電感串聯和電感并聯時總電感量怎么算呢？在了解互感電感串并聯之前，先必須知道電感的互感、互感系數等知識。

互感

1、互感電感的互感現象：如圖1所示，設兩個線圈L1和L2，當L1線圈通入交變電流時，在本線圈產生交變磁通Φ1，并引起自感電壓e1；同時，磁通穿過另一個線圈，產生相應互感電壓e2，這種現象稱為互感現象。

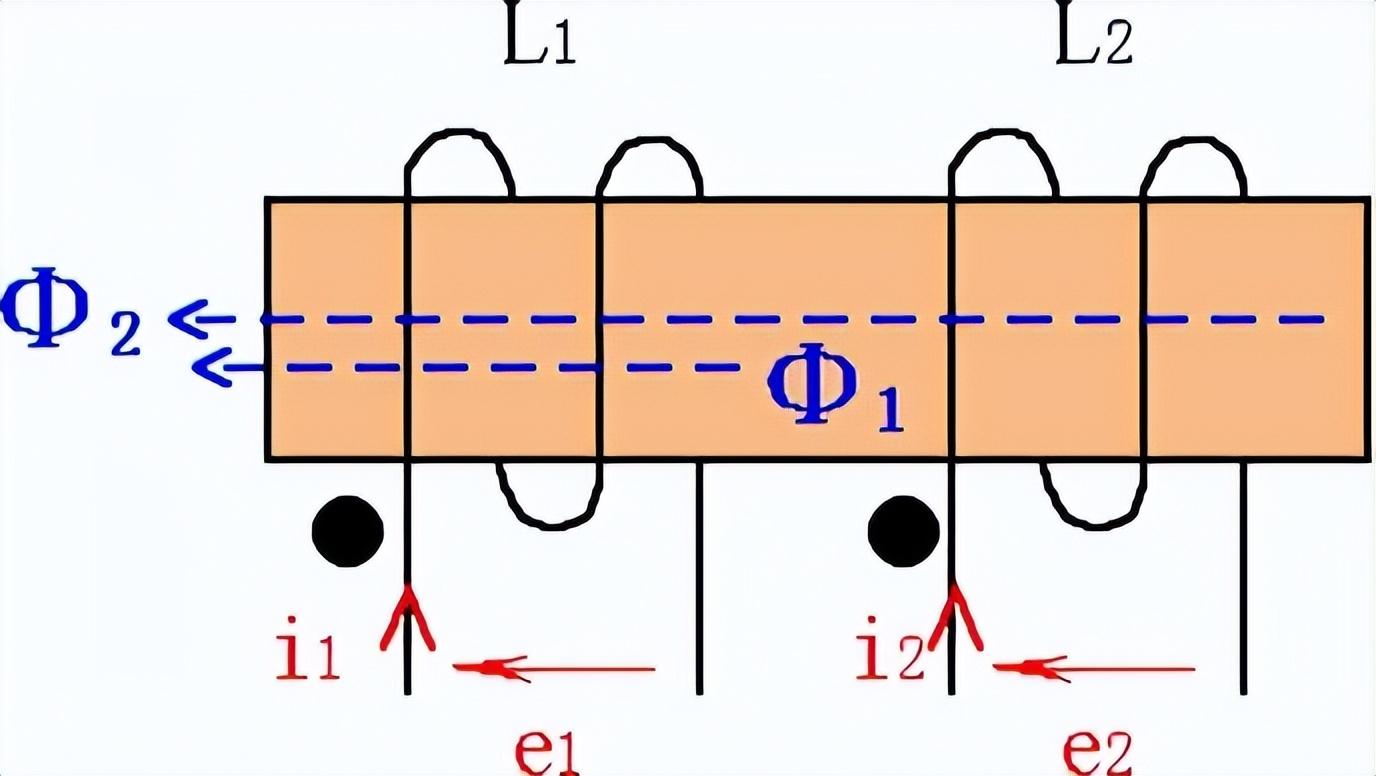
圖1 互感電感互感現象

2、互感系數M：互感電感中的“M”稱為互感系數，單位和自感系數L相同。

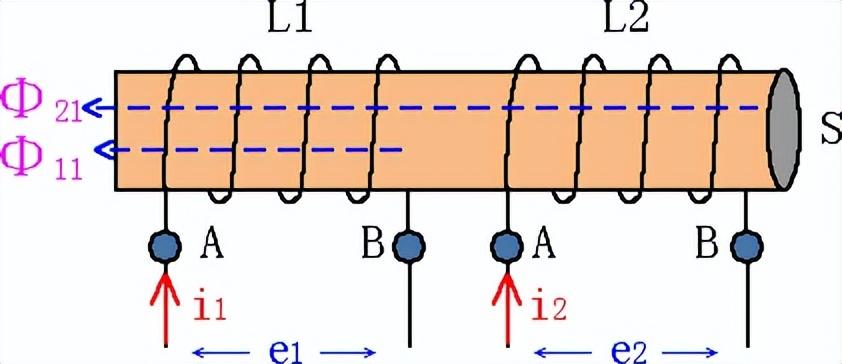
圖3 互感系數M

線圈L1中的電流i1變化，引起線圈L2的磁通變化，線圈L2中產生感應電動勢e2。穿過線圈2的磁通量ψ21正比于線圈L1中電流i1。

我們定義：

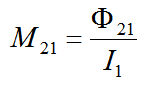
M21是線圈1對線圈2的互感系數，單位亨(H)

那么對于L2、i2一樣，則有

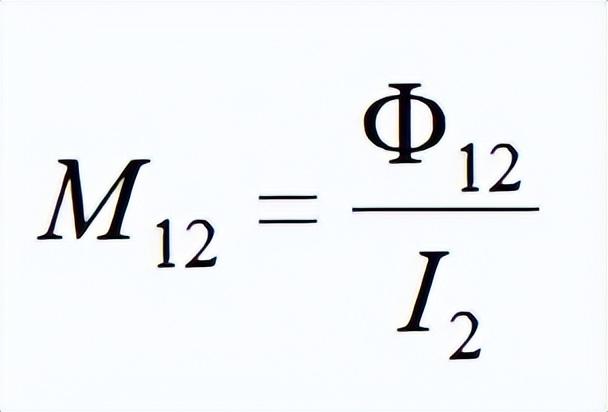
M12表示線圈2對線圈1的互感

若兩回路相對位置不變，周圍無鐵磁性物質，則互感系數M=M21=M12，則

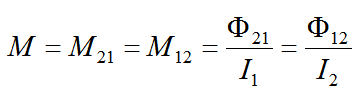
注意：中Φ21為通過線圈2的磁通量，I1為通過線圈1的電流：中Φ12為通過線圈1的磁通量，I2為通過線圈2的電流

在工程上為了定量地描述兩個耦合線圈的耦合緊密程度，常用常數k表示耦合系數：

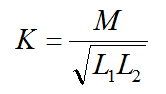
k表示耦合系數，M為互感系數，L1為線圈1電感量，L2為線圈2電感量

通常情況下：

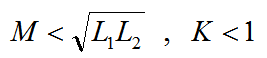
當一個線圈產生的磁通全部穿過另一個線圈，這種情況稱為全耦合即理想狀態K=1。

3、同名端與異名端：如圖4所示，繞在同一鐵心柱上，相對繞向相同的端子。各繞組的同名端，電流同時流入或者同時流出。用一對符號“?”予以標注。如下圖中1、3互為同名端，2、4互為同名端；1、4互為異名端，2、3互為異名端。互感電壓取“+”，反之取“-”。

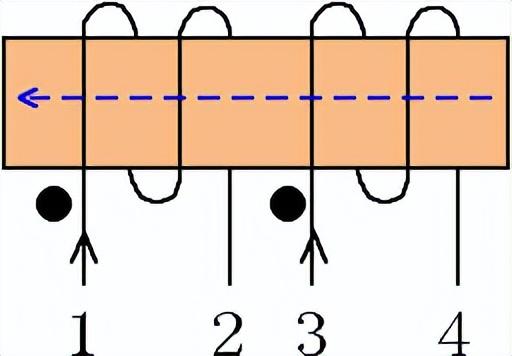
圖4 同名端與異名端

互感電感的串聯

由于同名端的存在，具有互感的兩個線圈串聯的電路，就有兩種接法： 即一種是同向串聯，如圖5所示，另一種是反向串聯，如圖6所示。

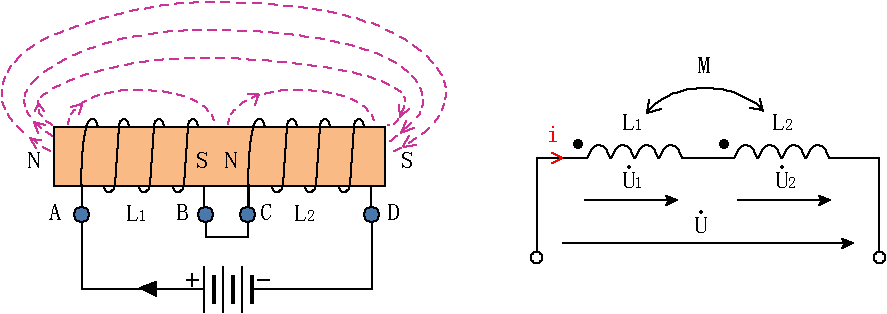
圖5 同向串聯

（1）同向串聯：如圖5所示。把兩線圈的異名端相連，電流從同名端流入、異名端流出，這種連接方式稱為同向串聯。

依據圖5中所示參考方向可列出兩線圈的伏安關系：

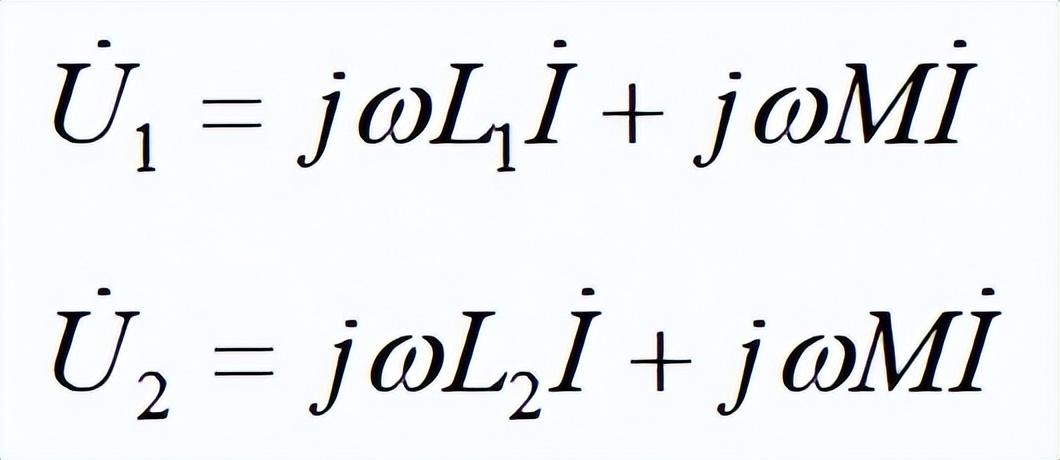
串聯后電路兩端總電壓為：

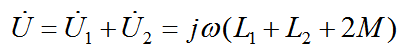
所以，當它們同相串聯的時候，對應的電感量為：

（2）反向串聯：如圖6所示。把兩線圈的同名端相連，電流從同名端流入、異名端流出，這種連接方式稱為反向串聯。

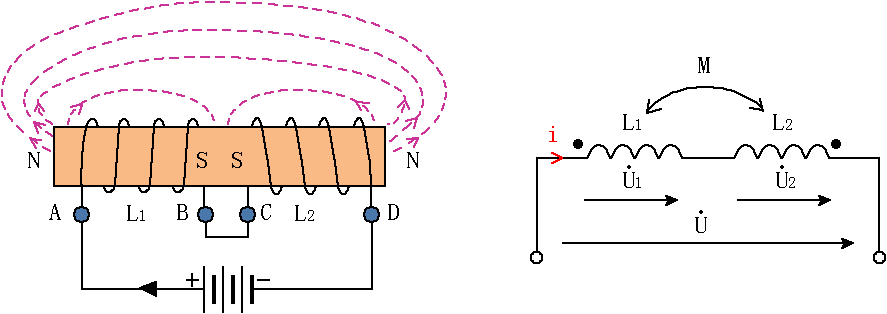
圖6 反向串聯

如果是反向串聯的時候，按照相同的方式，可以證明對應的等效電感量為：

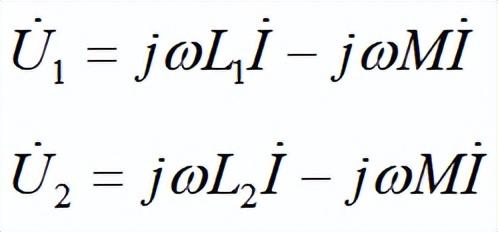
串聯后電路兩端總電壓為：

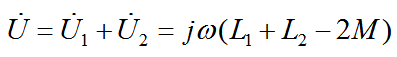
所以，當它們反向串聯的時候，對應的電感量為：

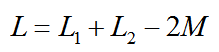
互感電感的并聯

兩個互感線圈并聯時，也有兩種情況，一種是兩個線圈同名端相連，稱同向并聯，如圖7(a)所示；另一種為兩個線圈的異名端相連，稱反向并聯，如圖7(b)所示。

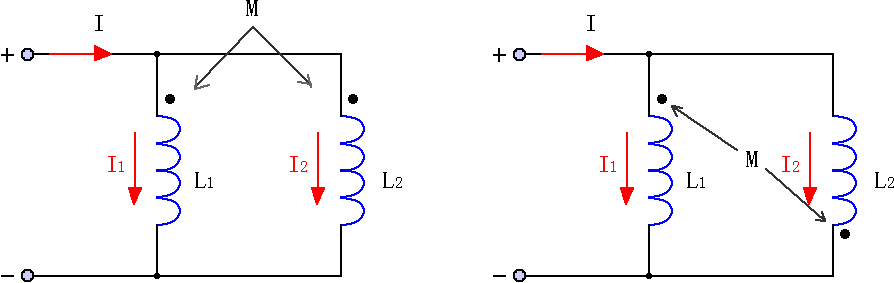
圖7(a) 圖7(b)

（1）同向并聯：當選擇電流為圖示參考方向時，則在正弦電路中有：

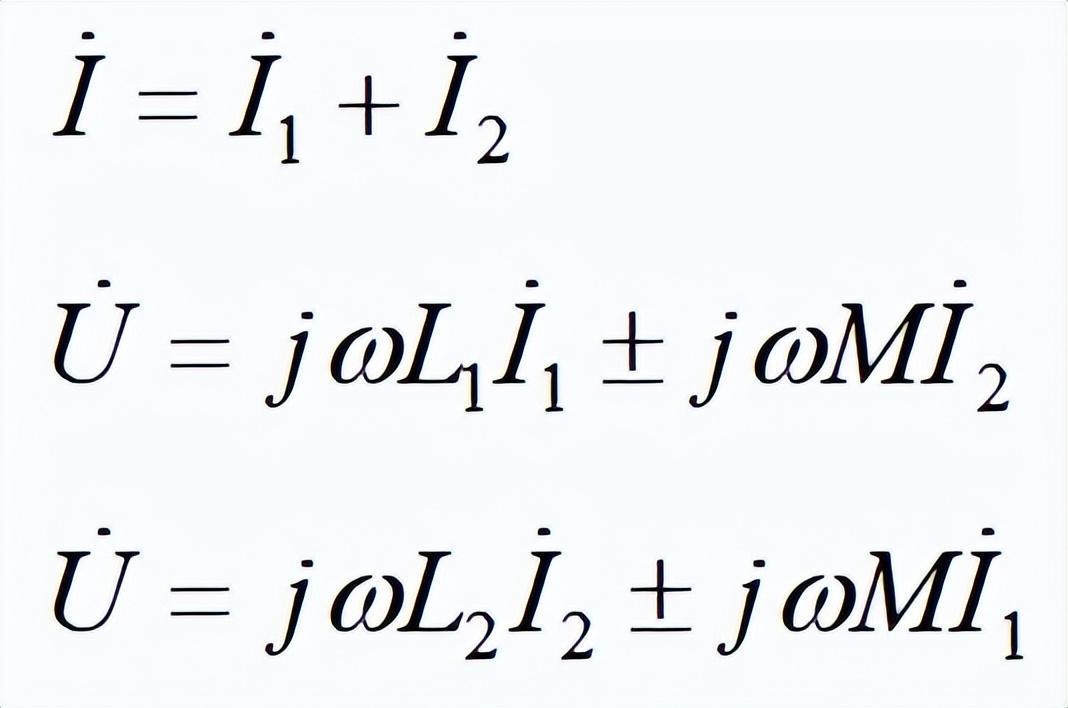
式中互感電壓前的正號對應于順并，負號對應于反并。求解可得并聯電路的等效復阻抗Z為：

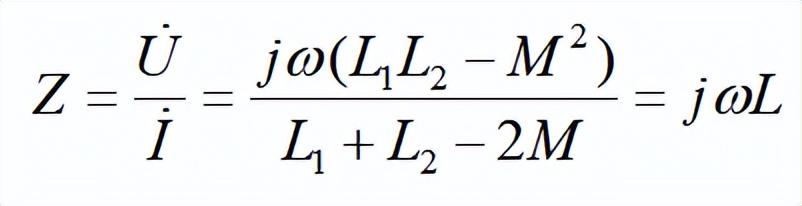
同向并聯的等效復阻抗Z

L為兩個線圈同相并聯后的等效電感，即

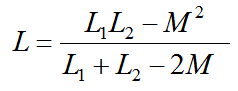
同向并聯等效電感

（2）反向并聯：如7(b)所示，式中互感電壓前的正號對應于順并，負號對應于反并。求解可得反向并聯電路的等效復阻抗Z為：

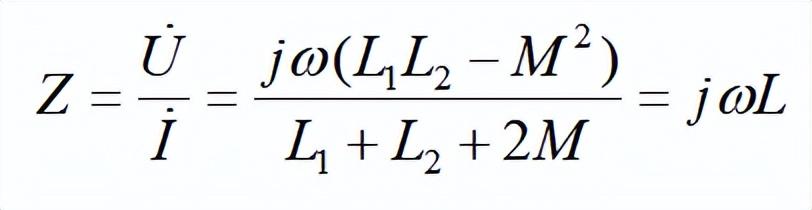
反向并聯電路等效復阻抗Z

L為兩個線圈反相并聯后的等效電感，即

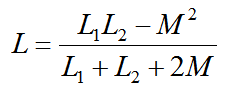
反相并聯等效電感

例題1：如圖8所示，兩個線圈電感L分別為0.1H、0.2H，互感系數為0.2H，求總電感。

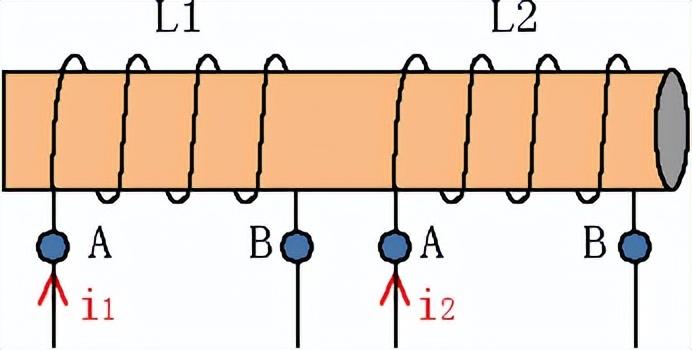
圖8

解：兩個串聯電感是同向串聯，則等效互感電感L為：

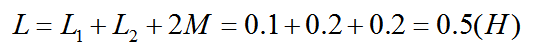
例題2：如圖9所示為理想互感電感，兩個線圈為電感L分別為0.2H、0.8H，求互感系數和總電感。

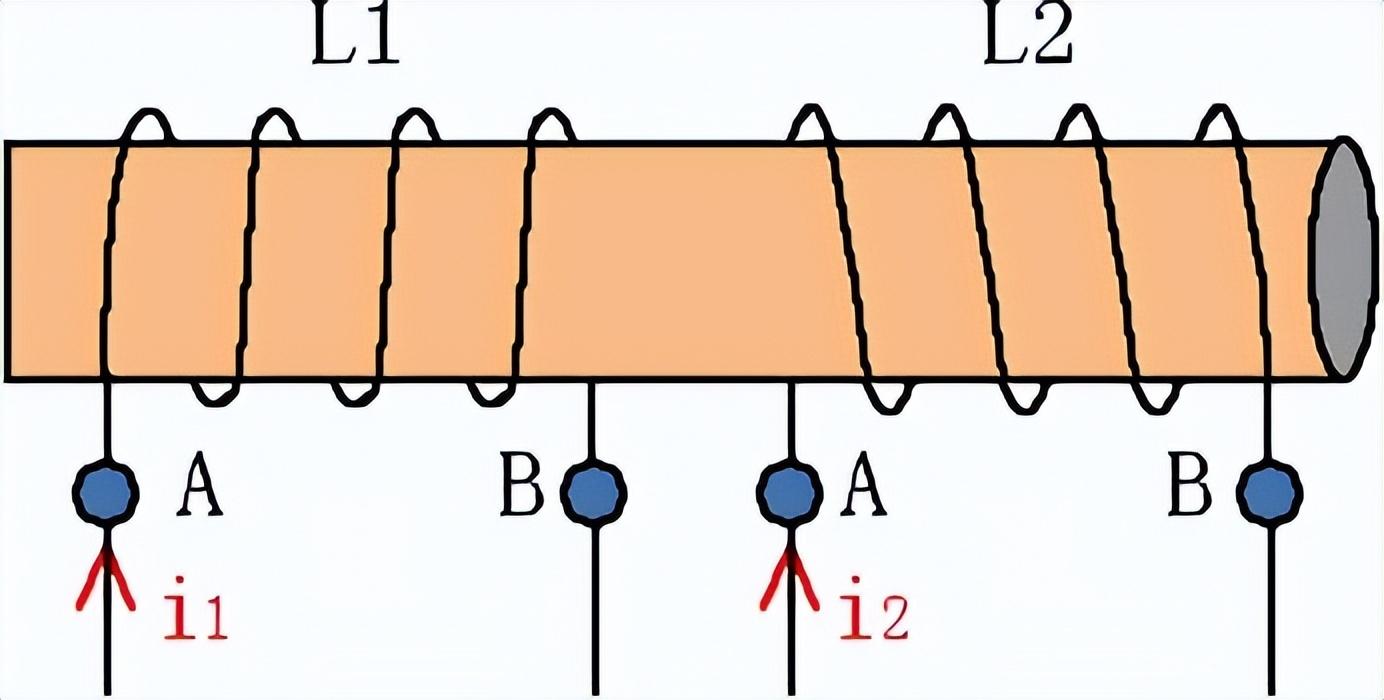
圖9

解：由于是理想互感電感，則耦合系數K=1，則互感系數為：

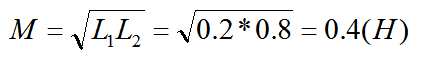
由于兩個串聯電感是反向串聯，則等效互感電感L為：

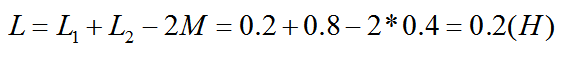
例圖分析：如圖10所示，線圈電感L1分別為0.2H，互感系數為0.4H，總電感為0.6H，求電感L2大小。答案在評論區見！

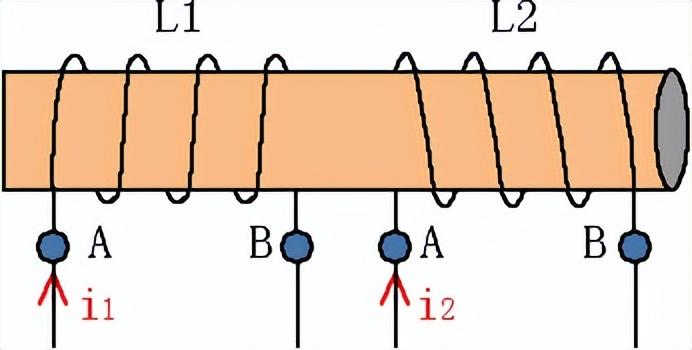
圖10