電子發燒友App
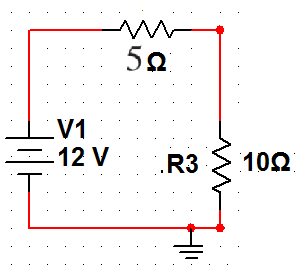
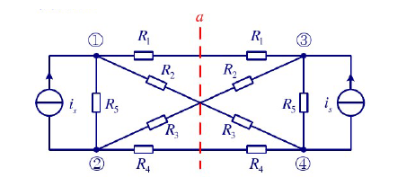
進行電路分析時，有些電路具有對稱性。 利用其對稱性可以化簡電路求解。 如圖1所示電路，沿中間R3支路對折后，兩部分電路完全重合，這樣的電路就是對稱電路，R3支路為其對稱軸。 對稱電路對折后，重合的點為對稱點，對稱點的電位相等。
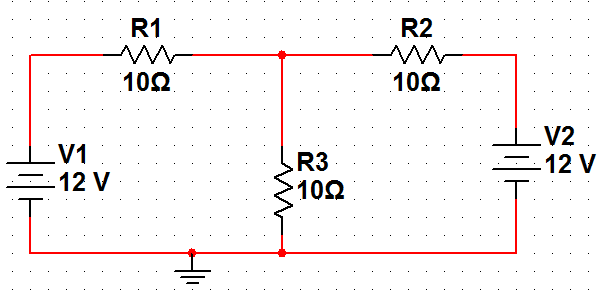
圖1 對稱電路
對圖1所示電路，可以把R3支路等效成兩個2R3支路并聯，如圖2（a）所示，中間虛線為其對稱軸。 對折后重合的點為對稱點。 對稱點具有相同的電位，是等點位點。 電路中等電位點的連線可以去掉，因為其上電流為零。 圖2（a）中兩個20Ω電阻支路端部的連線去掉后，電路如圖2（b）所示。 由此可算得R1、R2支路電流為0.4A，R3兩端電壓為8V。
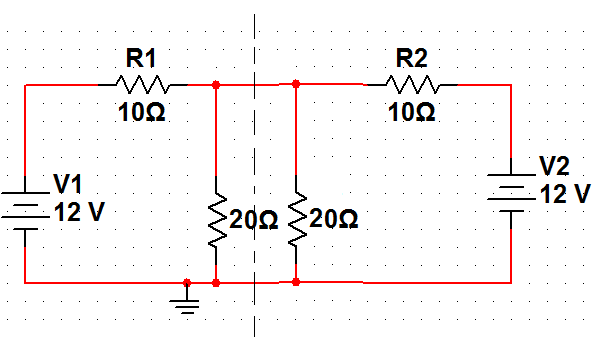
（一）
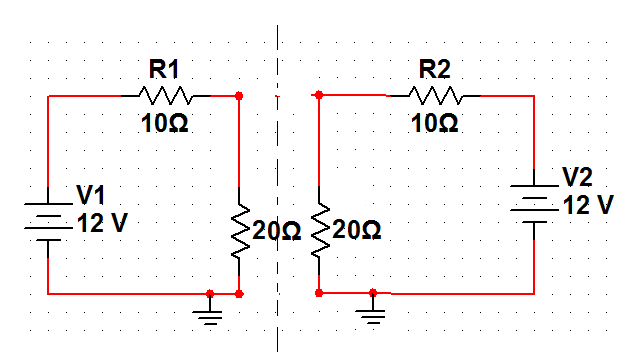
（二）
圖2 對稱電路等電位點斷開
等電位點也可以用短路線連接，對原電路無影響。 把圖1電路的對稱點用短路線連起來，如圖3（a）虛線所示，其等效電路如圖3（b）所示，其中5Ω電阻為R1、R2兩個10Ω電阻并聯后的等效電阻。 兩個12V電壓源并聯后等效成一個12V電源。 由該電路也可算得R3兩端電壓為8V。
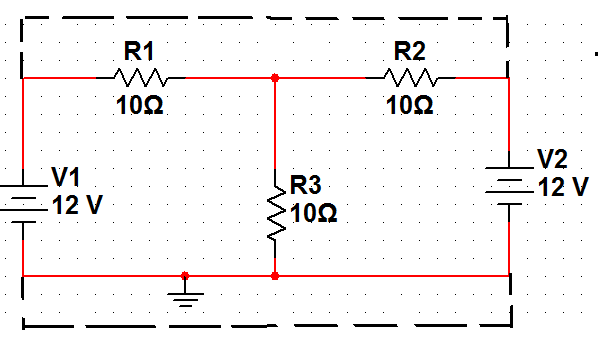
（一）
（二）
圖3 對稱電路等電位點用短路線連接
綜上，對稱電路，可以利用對稱性化簡求解。
工商網監
評論