電路的諧振現象
為了更好地理解諧振式電源,這里回憶一下電路諧振的條件及其特點。
一、串聯電路的諧振
一個R、L、C串聯電路,在正弦電壓作用下,其復阻抗:
Z=R+j(ωL-1/ωC)
一定條件下,使得XL=XC,即ωL=1/ωC ,Z=R,此時的電路狀態稱為串聯諧振。
明顯地,串聯諧振的特點是:
1.阻抗角等于零,電路呈純電阻性,因而電路端電壓U和電流I同相。
2.此時的阻抗最小,電路電流有效值達到最大。
3.諧振頻率:ωo=1/√LC 。
4.諧振系數或品質因素:
Q=ωoL/R=1/ωoCR=(√L/C)/R。
由于串聯諧振時,L、C電壓彼此抵消,因此也稱為電壓諧振。從外部看,L、C部分類似于短路。
而此時Uc、UL是輸入電壓U的Q倍。Q值越大,振蕩越強。
這里的Z0=√L/C,我們稱為特性阻抗,它決定了諧振的強度。
5.諧振發生時,C、L中的能量不斷互相轉換,二者之間反復進行充放電過程,形成正弦波振蕩。
二、并聯電路的諧振
一個R、L、C并聯電路,在正弦電壓作用下,其復導納:
Y=1/R-j(1/ωL-ωC)
一定條件下,使得YL=YC,即1/ωL=ωC ,Y=1/R,此時的電路狀態稱為并聯諧振。
明顯地,串并諧振的特點是:
1.導納角等于零,電路呈純電阻性,因而電路端電壓U和電流I同相。
2.此時的導納最小,電路電流有效值達到最小。
3.諧振頻率:ωo=1/√LC 。
4.由于并聯諧振時,L、C電流彼此抵消,因此也稱為電流諧振。從外部看,L、C部分類似于開路,L、C各自有效電流卻達到最大。
5.諧振發生時,C、L中的能量不斷互相轉換,二者之間反復進行充放電過程,形成正弦波振蕩。
諧振式電源的基本原理
諧振式電源是新型開關電源的發展方向。它利用諧振電路產生正弦波,在正弦波過零時切換開關管,從而大大提高了開關管的控制能力,并減小了電源體積。同時,也使得電源諧波成分大為降低。另外,電源頻率得到大幅度提高。PWM一般只能達到幾百K,但諧振開關電源可以達到1M以上。
普通傳統的開關電源功率因素在0.4-0.7,諧振式電源結合功率因素校正技術,功率因素可以達到0.95以上,甚至接近于1。從而大大抑制了對電網的污染。
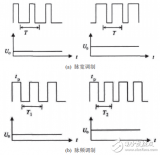
這種開關電源又分為:
1.ZCS——零電流開關。開關管在零電流時關斷。
2.ZVS——零電壓開關。開關管在零電壓時關斷。
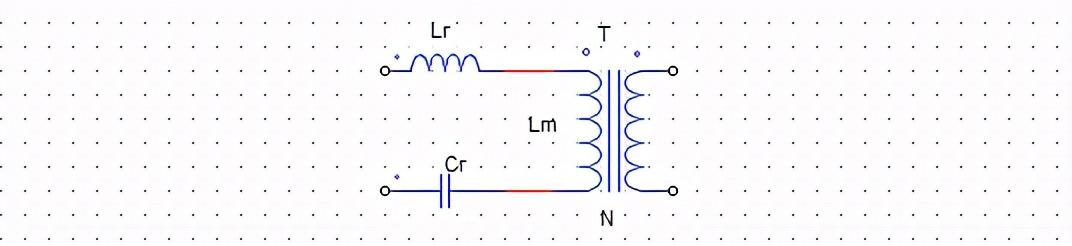
在脈沖調制電路中,加入L、C諧振電路,使得流過開關的電流及管子兩端的壓降為準正弦波。下面是這兩種開關的簡單原理圖。
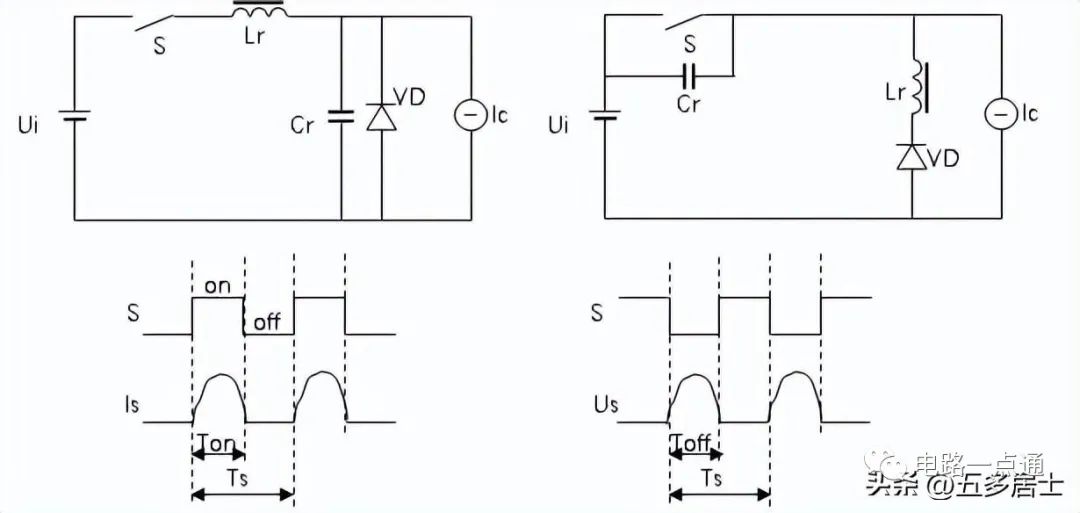
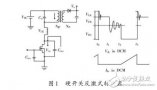
圖1:電流諧振式開關電路 電壓諧振式開關電路
ZCS電流諧振開關中,Lr、Cr構成的諧振電路通過Lr的諧振電流通過S,我們可以控制開關在電流過零時進行切換。這個諧振電路的電流是正弦波,而Us為矩形波電壓。
ZVS電壓諧振開關中,Lr、Cr構成的諧振電路的Cr端諧振電壓并聯到S,我們可以控制開關在電壓過零時進行切換。這個諧振電路的電壓是正弦波,而Is接近矩形波。
以上兩種電路,由于開關切換時,電流、電壓重疊區很小,所以切換功率也很小。
以上開關電源是半波的,當然也可以設計成全波的。所以又有半波諧振開關和全波諧振開關的區分。
諧振開關的動態過程分析
實際上,諧振開關中的所謂“諧振”并不是真正理論上的諧振,而是L、C電路在送電瞬間產生的一個阻尼振蕩過程。下面,我們對這個過程做一些分析,以了解諧振開關的工作原理。
一、零電流開關
實際的零電流開關諧振部分拓補又分L型和M型。如下面兩組圖形所示:
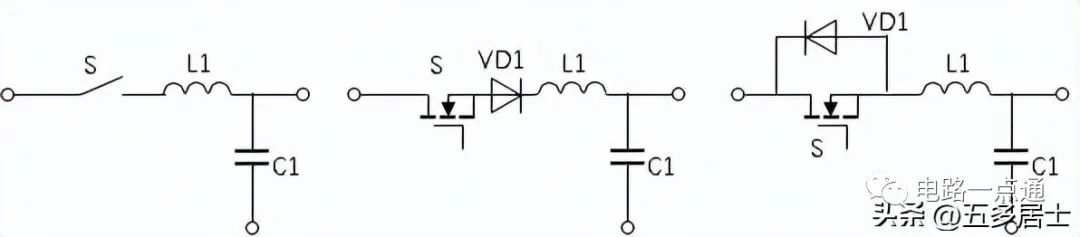
圖2:L型零電流諧振開關(中半波,右全波)
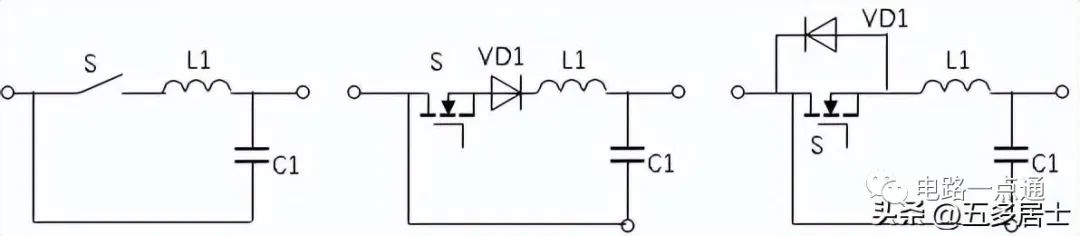
圖3:M型零電流諧振開關(中半波,右全波)
這里的L1用于限制di/dt,C1用于傳輸能量,在開關導通時,構成串聯諧振。用零電流開關替代PWM電路的半導體開關,可以組成諧振式變換器電路。按照Buck電路的拓補結果,可以得到如下電路:
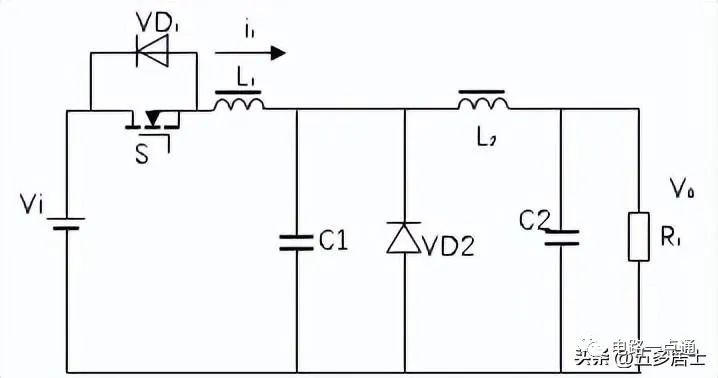
圖4:Buck型準諧振ZCS變換器(L型)
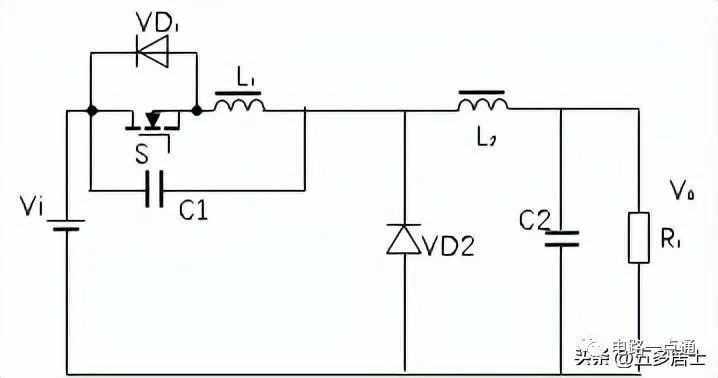
圖5:Buck型準諧振ZCS變換器(M型)
這里,我們分析一下L型電路的工作過程。
假定這是一個理想器件組成的電源。L2遠大于L1,從L2左側看,可以認為流過L2、C2、RL的輸出電流是一個恒流源,電流I0。諧振角頻率:
ω0=1/√L1C1 。
特性阻抗:
Z0 =√L1/C1)。
動態過程如下:
1.線性階段(t0-t1):
在S導通前,VD2處于續流階段。此時VVD2=VC1=0。S導通時,L1電流由0開始上升,由于續流沒有結束,此時初始VL1=Vi。
由VL1=Vi=L1di/dt,且L1初始電流為0,有:
i1=Vi(t-t0)/L1
----------------------------------式1
到t1時刻,達到負載電流I0,因此:
此階段持續時間:
T1=t1-t0=L1I0/Vi
由式1,可以看出,此階段i1是時間的線性函數。
2.諧振階段(t1-t2):
在電流i1上升期間,當i1小于I0時,由于i1無法供應恒流I0,續流過程將維持。當i1=I0時,將以i1-I0對C1充電,VD2開始承受正壓,VD2電流下降并截止。L1、C1開始串聯諧振,i1 因諧振繼續上升。
iC1=C1dVC1/dt=i1-I0
VL1=L1di1/dt=Vi-VC1
因而:
i1=I0+ iC1=I0+Vi/Z0*sinω0 (t-t1)------------------式2
其中,iC1為諧振電流。
VC1=Vi-VL1= Vi -Vicosω0 (t-t1)= Vi [1-icosω0 (t-t1)]--式3
諧振到ta時刻,諧振電流歸零。如為半波開關,則開關自行關斷;如果是全波開關,開關關斷后,將通過VD1進行阻尼振蕩,將電容能量饋送回電源,到時刻tb電流第二次為0。本階段結束,這時的時刻為t2。
VC1在i1諧振半個周期,i1=I0時,達最大值。i1第一次過零(ta)時,S斷開。如為半波開關,則諧振階段結束。如為全波開關,C1經半個周期的阻尼振蕩到電流為0(tb)時,將放電到一個較小值。
從式2、3,可以看出諧振階段ta前,i1、VC1是時間的正弦函數;如為全波開關,還有一段時間的阻尼振蕩波。
3.恢復階段(t2-t3):
由于VC1滯后1/4個諧振周期,因而在t2后,因L2的作用還將繼續向負載放電,直至VC1=0。這階段,如考慮電流方向性:
I0=-C1dVC1/dt
故:VC1= VC1(t2)-I0(t-t2)/C1
------------------------------------式4
因此,這個階段的VC1是時間的線性函數,電壓從VC1(t2)逐步下降到零。如為半波開關,則開關分壓也將線性上升到輸入電源值。
4.續流階段(t3-t4):
當電容放電到零后,VD2因反壓消失而導通,對L2及負載進行續流,以保持電流I0連續。
此時,我們可以根據電路的要求,選擇在適當時間再次開通S,重新開始線性階段。
根據以上導出的各公式,可以得到如下的波形圖:
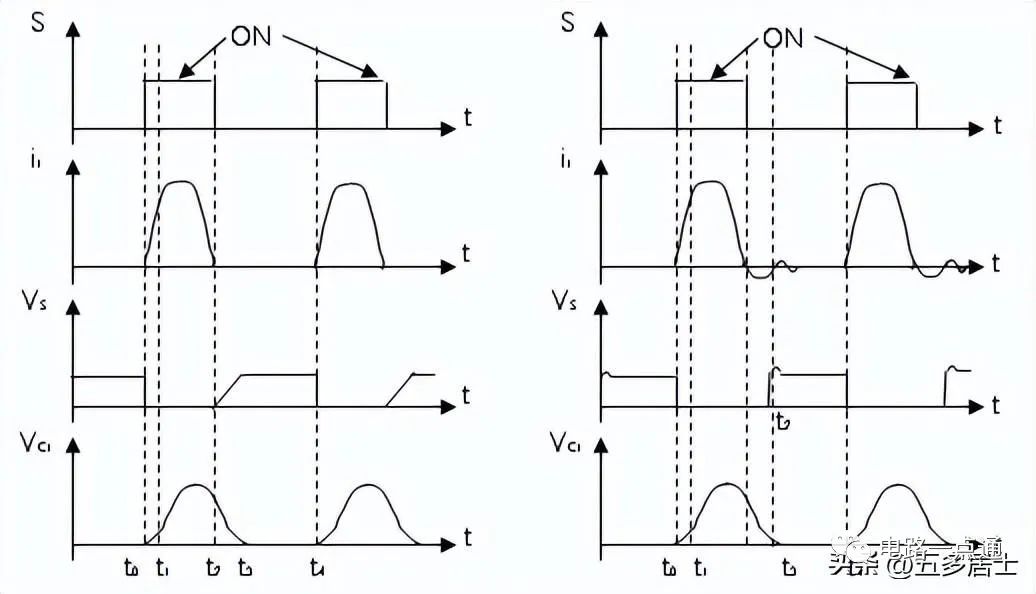
圖2-18:半波ZCS開關波形 全波ZCS開關波形
從以上分析可以看出,ZCS諧振開關變換器的開關管總是在電流為0時進行切換。
實際情況與理想分析有所不同,VC1將有所超前。
M型電路分析方法類似,不再贅述。
二、零電壓開關
ZCS在S導通時諧振,而ZVS則在S截止時諧振,二者形成對偶關系。分析過程大體類似,此處從略。
綜合以上分析過程,我們可以看出,該拓補諧振結構只能實現PFM調節,而無法實現PWM。原因是脈沖寬度僅受諧振參數控制。要實現PWM,還需要增加輔助開關管。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App











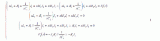











評論