運算放大器之所以被稱為運算放大器，沒有叫A放大器或者B放大器，那是因為這種結構可以做運算，比如積分，微分，加法，減法呀等等。

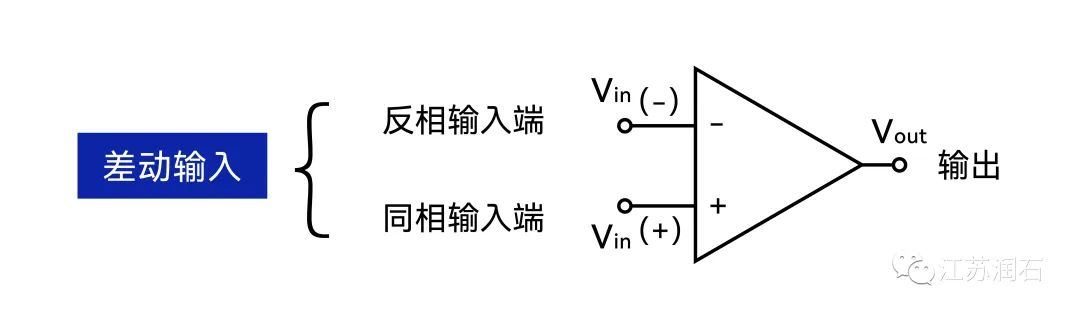
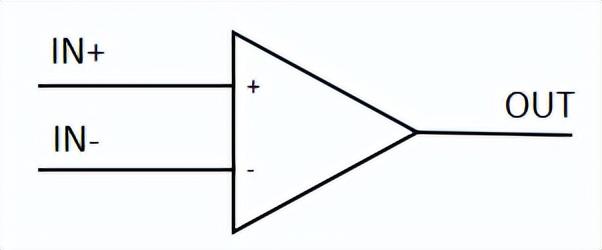
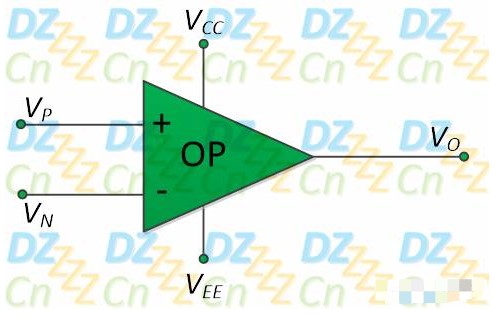
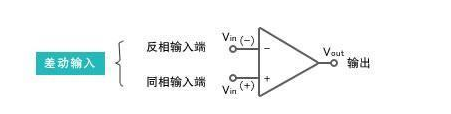
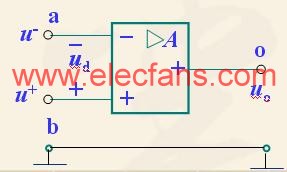
運算放大器有兩個輸入，一個為同相輸入(non-inverting input)，記為V+，一個為反相輸入(inverting input)，記為V-。

運算放大器有一 個輸入，記為Vout。

理想情況下，運算放大器只放大兩個輸入之間的電壓差。

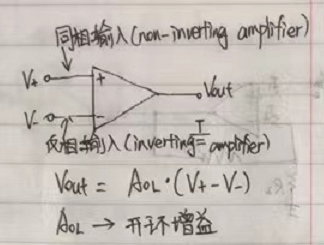
那為啥運算放大器會有兩個輸入呢？這是因為兩個輸入有兩個輸入的優點。

(1) 兩個輸入可以建立只有一個輸入時無法完成的電路；

(2) 有時候，若遇到一個復雜系統(比如包括很多晶體管以及級數)，將其等效為運放，可以簡化分析。

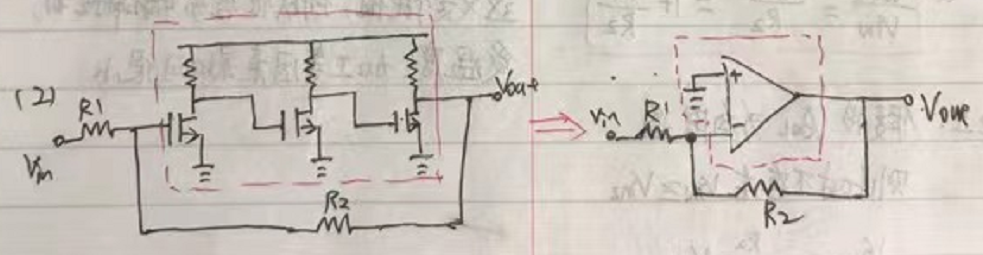
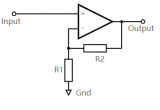
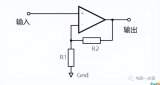
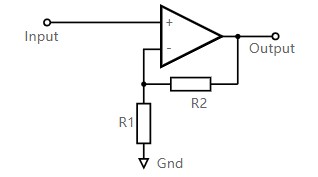
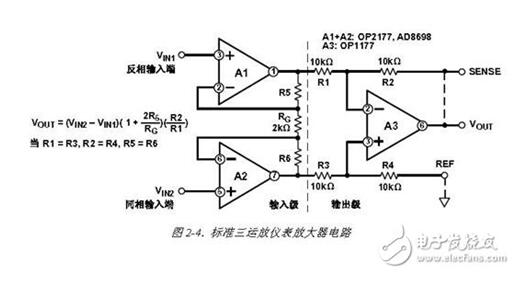
比如說，下圖中左側，覺得這電路，因為反饋電阻R2的存在，頓時覺得復雜。但是如果將三級放大電路等效為運放，那看上去就簡單明了了。

我們希望運放是理想的，但是理想豐滿，現實總是骨感的。所以實際的運放，總會有很多的不完美。

理想的運放：

開環增益為∞；輸入阻抗為∞；輸出阻抗為0；帶寬為∞。

但實際的運放：

開環增益有限；輸入阻抗雖大，但不是∞；輸出阻抗雖小，但不是0；帶寬有限。

運放的虛短，虛斷

因為Vout=Aol*(V+-V-)，因為Vout為有限值，而Aol的值很大，那么V+與V-相差很小，即V+~==V-.這就是所謂的虛短。

而因為運算放大器是輸入阻抗很高，雖然連線連著，但是電流極小，可以認為為0，即I+=0,I-=0,因此可以認為兩個輸入與運放是斷開的，這就是所謂的虛斷。

虛短和虛斷這兩個概念，在運算電路分析中，是常用的。

運算的基本電路

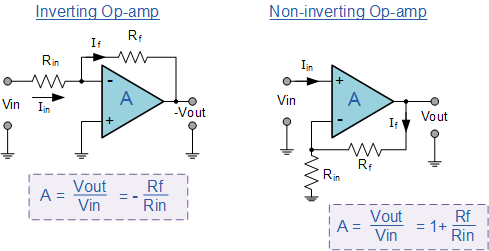
同相放大器(Non-inverting amplifier)

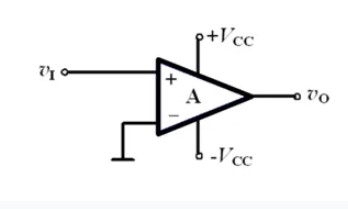
上圖中Aol稱為開環增益，而Vout/Vin則稱為閉環增益。

運算放大器構成的同相放大器，其增益與電阻的比值有關，這個特性優于普通放大器。因為電阻比是能夠精確控制的，而且受溫度，加工等因素的影響很小。

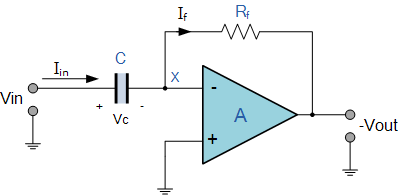
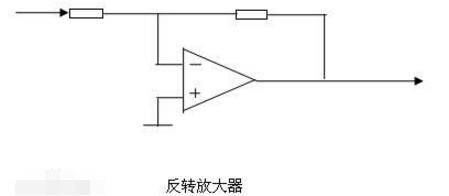
反相放大器(inverting amplifer)

可以看到，反相放大器的增益仍然是比值，可以精確控制。此時其輸入阻抗為R2，與同相放大器相比，輸入阻抗變小。而且，如果降低R2以獲得更高增益的同時，也降低了輸入阻抗。

這在使用反相放大器時，也需要考慮一下。

單位增益緩沖器(Unity-gain buffer)

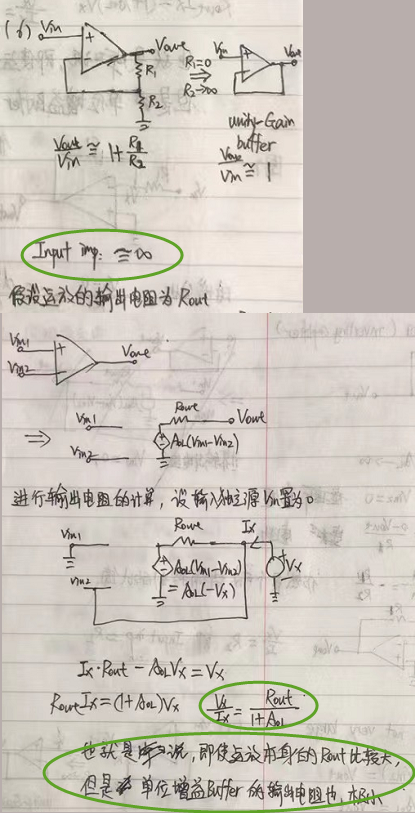
那單位增益緩沖器又有啥好處呢?也不能放大增益。

如果計算一下單位增益緩沖器的話，你會發現，其輸入阻抗接近于無窮大，輸出阻抗則接近于0(即使運放本身的輸出阻抗不小)。

這使得其可以在不對前級電路產生影響的情況下，感應到前級電路的電壓；同時，又能驅動低輸入阻抗的電路。

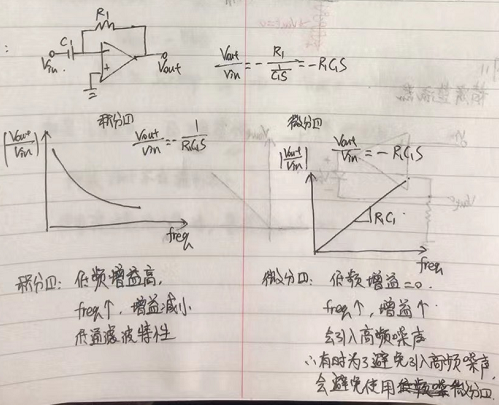
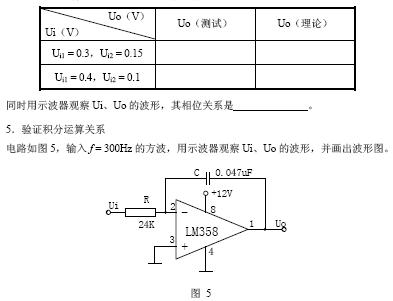
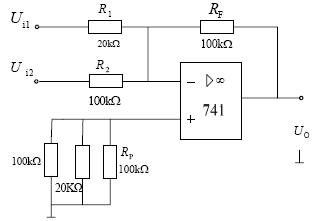
積分器

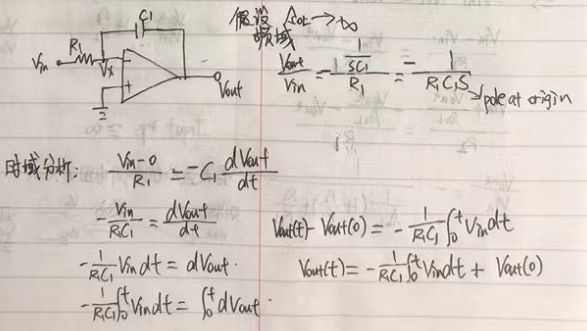
微分器

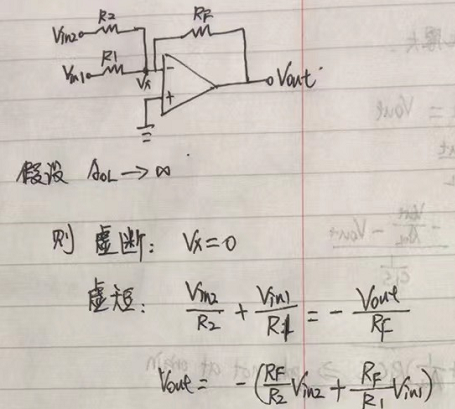
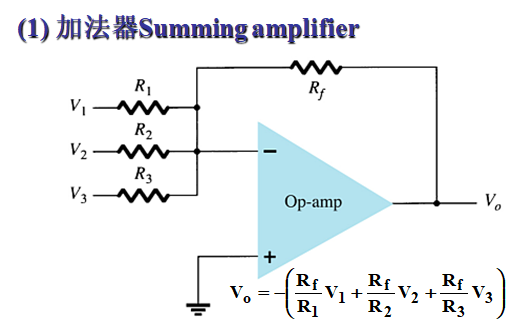
加法器

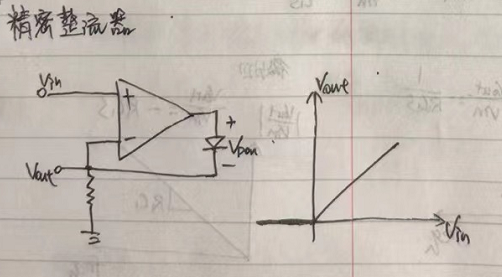
精密整流器

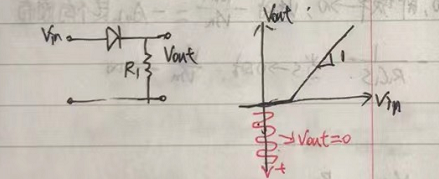
簡單的二極管整流器有一個問題，就是當輸入信號的幅度小于二極管的開啟電壓VDon時，輸出為0，如下圖所示。

由運放構成的精密整流器，不會存在這樣一個問題。

對數放大器

對數放大器的輸入輸出曲線如下圖所示。

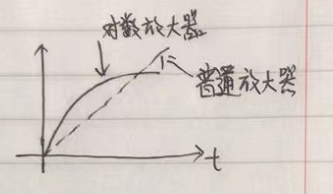
如果信號輸入幅度較小，則其放大增益大；當信號幅度增加時，其放大增益相應減小。

對數放大器的結構如下圖所示。

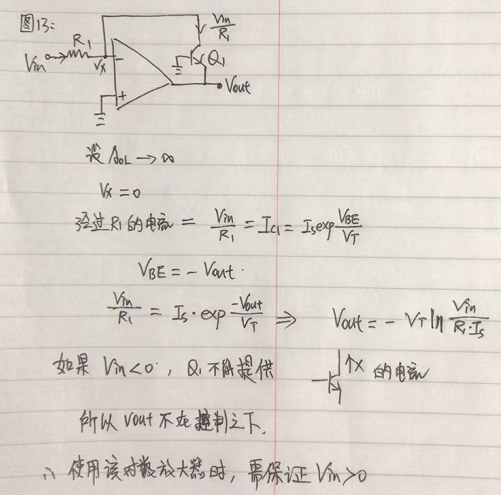
審核編輯：劉清