所謂聚類問題，就是給定一個元素集合D，其中每個元素具有n個可觀察屬性，使用某種算法將D劃分成k個子集，要求每個子集內部的元素之間相異度盡可能低，而不同子集的元素相異度盡可能高。其中每個子集叫做一個簇。

與分類不同，分類是示例式學習，要求分類前明確各個類別，并斷言每個元素映射到一個類別，而聚類是觀察式學習，在聚類前可以不知道類別甚至不給定類別數量，是無監督學習的一種。目前聚類廣泛應用于統計學、生物學、數據庫技術和市場營銷等領域，相應的算法也非常的多。

K-Means算法實例

例：以下是一組用戶的年齡數據，將K值定義為2對用戶進行聚類。并隨機選擇16和22作為兩個類別的初始質心。

Data_Age = ［15，15， 16， 19， 19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］;

CenterId1 =16， CenterId2 = 22

（1）、計算距離并劃分數據

通過計算所有用戶的年齡值與初始質心的距離對用戶進行第一次分類。計算距離的方法是使用歐式距離。距離值越小表示兩個用戶間年齡的相似度越高。

第一次迭代：

Data_Age = ［15，15， 16， 19， 19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］;

Distance（16）= ［1， 1， 0， 3， 3， 4， 4， 5， 6， 12， 19， 24， 25， 26， 27， 28，44， 45， 49］;

Distance（22）= ［7， 7，6， 3， 3， 2， 2， 1， 0， 6， 13， 18， 19， 20， 21， 22， 38， 39，43］;

Group1_（16）= ［15，15， 16］; Mean =15.33

Group2_（22）= ［19，19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 36.25

（2）、使用均值作為新的質心

將兩個分組中數據的均值作為新的質心，并重復之前的方法，迭代計算每個數據點到新質心的距離，將數據點劃分到與之距離較小的類別中。

第二次迭代：

Data_Age = ［15，15， 15.33， 16， 19， 19， 20， 20， 21， 22， 28，35， 36.25， 40， 41， 42， 43， 44， 60， 61， 65］;

Distance（15.33）=［0.33， 0.33， 0.67，3.67， 3.67， 4.67， 4.67， 5.67， 6.67， 12.67， 19.67， 24.67， 25.67， 26.67，27.67， 28.67， 44.67， 45.67， 49.67］;

Distance（36.25）=［21.25， 21.25， 20.25， 17.25， 17.25， 16.25，16.25， 15.25， 14.25， 8.25， 1.25， 3.75， 4.75， 5.75，6.75， 7.75， 23.75， 24.75， 28.75］;

Group1_（15.33）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22］; Mean = 18.56

Group2_（36.25）=［ 28， 35， 40， 41， 42， 43， 44， 60， 61，65］; Mean = 45.90

第三次迭代：

Data_Age = ［15，15， 16， 18.56， 19， 19， 20， 20， 21， 22， 28，35， 40， 41， 42， 43， 44， 45.90， 60， 61， 65］;

Distance（18.56）=［3.56， 3.56， 2.56，0.44， 0.44， 1.44， 1.44， 2.44， 3.44， 9.44， 16.44， 21.44， 22.44， 23.44，24.44， 25.44， 41.44， 42.44， 46.44］;

Distance（45.90）=［30.90， 30.90， 29.90， 26.90， 26.90， 25.90，25.90， 24.90， 23.90， 17.90， 10.90， 5.90， 4.90， 3.90，2.90， 1.90， 14.10， 15.10， 19.10］;

Group1_（18.56）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22， 28］; Mean = 19.50

Group2_（45.90）=［ 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 47.89

第四次迭代：

Data_Age = ［15，15， 16， 19， 19， 19.50， 20， 20， 21， 22， 28，35， 40， 41， 42， 43， 44， 47.89， 60， 61， 65］;

Distance（19.50）=［4.5， 4.5， 3.5，0.5， 0.5， 0.5， 0.5， 1.5， 2.5， 8.5， 15.5， 20.5， 21.5， 22.5， 23.5， 24.5，40.5， 41.5， 45.5］;

Distance（47.89）=［32.89， 32.89， 31.89， 28.89， 28.89， 27.89，27.89， 26.89， 25.89， 19.89， 12.89， 7.89， 6.89， 5.89，4.89， 3.89， 12.11， 13.11， 17.11］;

Group1_（19.50）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22，28］; Mean = 19.50

Group2_（47.89）=［ 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 47.89

（3）、算法停止條件

迭代計算每個數據到新質心的距離，直到新的質心和原質心相等，算法結束。

MATLAB中的kmeans函數

MATLAB中的kmeans函數采用的是將N*P的矩陣X劃分為K個類，使得類內對象之間的距離最大，而類之間的距離最小。

使用方法：

Idx = Kmeans（X，K）

［Idx， C］ = Kmeans（X，K）

［Idc， C， sumD］ = Kmeans（X，K）

［Idx， C， sumD， D］ = Kmeans（X，K）

各輸入輸出參數介紹：

X---N*P的數據矩陣

K---表示將X劃分為幾類，為整數

Idx---N*1的向量，存儲的是每個點的聚類標號

C---K*P的矩陣，存儲的是K個聚類質心位置

sumD---1*K的和向量，存儲的是類間所有點與該類質心點距離之和

D---N*K的矩陣，存儲的是每個點與所有質心的距離

［┈］ = Kmeans（┈，’Param1’，’Val1’，’Param2’，’Val2’，┈）

其中參數Param1、Param2等，主要可以設置為如下：

1、’Distance’---距離測度

‘sqEuclidean’---歐氏距離

‘cityblock’---絕對誤差和，又稱L1

‘cosine’---針對向量

‘correlation’---針對有時序關系的值

‘Hamming’---只針對二進制數據

2、’Start’---初始質心位置選擇方法

‘sample’---從X中隨機選取K個質心點

‘uniform’---根據X的分布范圍均勻的隨機生成K個質心

‘cluster’---初始聚類階段隨機選取10%的X的子樣本（此方法初始使用’sample’方法）

Matrix提供一K*P的矩陣，作為初始質心位置集合

3、’Replicates’---聚類重復次數，為整數

MATLAB代碼：

% KMeans算法的基本思想是初始隨機給定K個簇中心，按照最鄰近原則把待分類樣本點分到各個簇。

% 然后按平均法重新計算各個簇的質心，從而確定新的簇心。一直迭代，直到簇心的移動距離小于某個給定的值。

% 隨機獲取200個點

X = ［randn（50，2）+［-ones（50，1）， +ones（50，1）］; randn（50，2）+［ones（50，1）， ones（50，1）］; 。。。

randn（50，2）+［ones（50，1）， -ones（50，1）］; randn（50，2）+［-ones（50，1），-ones（50，1）］］;

%{

MATLAB中的kmeans函數采用的是將N*P的矩陣X劃分為K個類，使得類內對象之間的距離最大，而類之間的距離最小。

使用方法：

Idx = Kmeans（X，K）

［Idx，C］ = Kmeans（X，K）

［Idc，C，sumD］ = Kmeans（X，K）

［Idx，C，sumD，D］ = Kmeans（X，K）

各輸入輸出參數介紹：

X---N*P的數據矩陣

K---表示將X劃分為幾類，為整數

Idx---N*1的向量，存儲的是每個點的聚類標號

Ctrs---K*P的矩陣，存儲的是K個聚類質心位置

sumD---1*K的和向量，存儲的是類間所有點與該類質心點距離之和

D---N*K的矩陣，存儲的是每個點與所有質心的距離

%}

opts = statset（‘Display’，‘final’）;

［Idx，Ctrs，SumD，D］ = kmeans（X，4，‘Replicates’，4，‘Options’，opts）;

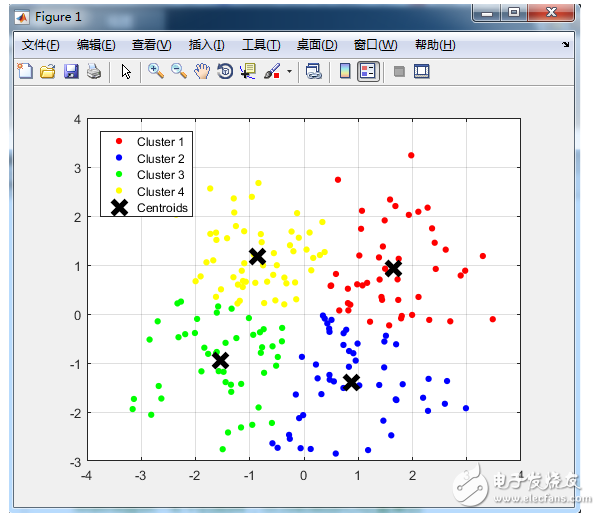
% 畫出聚類為1的點。

% X（Idx==1，1），為第一類的樣本的第一個坐標；X（Idx==1，2）為第一類的樣本的第二個坐標

plot（X（Idx==1，1）， X（Idx==1，2）， ‘r.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==2，1）， X（Idx==2，2）， ‘b.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==3，1）， X（Idx==3，2）， ‘g.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==4，1）， X（Idx==4，2）， ‘y.’， ‘MarkerSize’， 14）;

hold on;

% 繪出聚類中心點，kx表示是交叉符

plot（Ctrs（：，1）， Ctrs（：，2）， ‘kx’， ‘MarkerSize’， 14， ‘LineWidth’， 4）;

legend（‘Cluster 1’， ‘Cluster 2’， ‘Cluster 3’， ‘Cluster 4’， ‘Centroids’， ‘Location’， ‘NW’）;

grid on;

%{

［┈］ = Kmeans（┈，’Param1’，’Val1’，’Param2’，’Val2’，┈）

其中參數Param1、Param2等，主要可以設置為如下：

1、‘Distance’---距離測度

‘sqEuclidean’---歐氏距離

‘cityblock’---絕對誤差和，又稱L1

‘cosine’---針對向量

‘correlation’---針對有時序關系的值

‘Hamming’---只針對二進制數據

2、‘Start’---初始質心位置選擇方法

‘sample’---從X中隨機選取K個質心點

‘uniform’---根據X的分布范圍均勻的隨機生成K個質心

‘cluster’---初始聚類階段隨機選取10%的X的子樣本（此方法初始使用’sample’方法）

Matrix提供一K*P的矩陣，作為初始質心位置集合

3、‘Replicates’---聚類重復次數，為整數

%}