能源問題是當今世界廣泛關注的熱點問題，各國研究人員一直在努力尋找和開發新能源。近年來，環境振動能量已成為研究者的“ 新寵”，被應用在無線傳感器網絡的供電系統中，用以取代傳統的電池供電。

　　壓電能量采集因其具有轉化效率高、結構簡單、易于實現機構的微小化等諸多優點而成為振動能量采集研究的熱點。然而壓電陶瓷片在振動環境中僅能輸出低功率、小電流的交流電，無法直接為電子器件供電。通常需要設計附加的能量采集電路，以便完成交直流轉換和能量存儲。如何盡可能提升能量采集電路的能量傳遞效率是該類電路研究中關心的主要問題。

　　最早的能量采集電路由二極管橋式整流和大電容濾波構成。它被成為AC-DC 標準能量采集電路SEH（Standard Energy Harvesting），但該電路能量傳遞效率偏低，尤其是對機電耦合系數較低的能量采集裝置而言。為此，Guyomar 等人提出了電感同步開關采集電路SSHI（ Synchronized Switch Harvesting onInductor），由于該電路設計可大幅提升能量傳遞效率，已成為當前能量采集電路設計的主流方式。

　　需要指出的是，傳統SSHI電路的原理是在振動位移達到最大或最小時，閉合開關使電壓翻轉。為了協調控制開關閉合，需要用外接供電的傳感器檢測位移，并用控制器控制開關，顯然這種工作方式在采集能量的同時，還會消耗能量，有悖于環境能量采集的研究初衷。針對該問題，本文提出了一種完全不依賴外部檢測與控制設備的自感知型電感同步開關能量采集電路SS-SSHI（ Self-Sensing Synchronized Switch Harvesting on Inductor）。該電路的優點是僅依靠模擬電路即可完成檢測和控制，避免了對外界設備和能量的依賴。在該電路中，壓電片既是能量采集元件，又是傳感檢測元件，依靠其輸出電壓的峰值檢測與比較，可自動控制開關的閉合時機。同時，采用了一種模擬電子開關技術實現開關閉合。文中給出了電路的工作原理與功率分析，理論和實驗研究表明，相比于標準電路，SS-SSHI 電路即能顯著提高能量采集效率，又可避免對外界設備和能量的依賴。

　　1 壓電振子電學模型

　　壓電振子的電學模型可以等效為一個電流源和等效電容并聯，如圖1 所示。圖中Cp 為壓電片的夾持電容，Rp為壓電片等效內部電阻，一般為幾十兆歐或更大，ieq為等效電流源電流，可視為恒流源。

　　圖1 壓電能量采集模型

　　假設壓電振子的等效電流源的電流為ieq，那么它和振動速度關系如下：

　　其中αe 是外力—電壓因子，x（t）為壓電振子位移。

　　2 壓電振子電學模型

　　壓電振子一般產生的都是交流電，而我們要供電的負載大部分則是要求直流電，這就使得在給外界負載供電之前需要對其進行整流，提高能量采集效率是該類電路設計中首要考慮的問題。

　　2.1 標準能量采集電路

　　標準能量采集電路SEH（ Standard Energy Harvesting）是最常見的轉換電路。它由標準的整流電路和濾波電容構成，一般選擇的濾波電容C r 要足夠大以保證整流電壓V DC 是一個保持不變的直流電壓，即時間常數RCr遠大于振蕩周期。電路原理圖如圖2 所示。

　　圖中C r為濾波電容，RL為等效負載，電路輸出功率等于負載的輸入功率。如果壓電片電壓| Vp| DC，那么當| Vp | 達到VDC 時，整流橋導通，壓電片電壓此時就在| Vp | = VDC 處停止上升。當| Vp | 開始下降時，整流橋又開始斷開，電路處于斷開狀態。

　　圖2 標準能量采集電路

　　電容兩端電壓和電量的關系為：

　　q =C ● V （2）

　　式中q 為電容兩端電荷，C 為電容大小，V 為電容兩端電壓。

　　當電容兩端電壓為固定值時，電容上儲存的能量W 為：

　　W =V ● q （3）

　　根據（2）和（3） 可以得出標準電路的能量采集功率PSEH為：

　　這里f0 =ω/2π是振動頻率，Cp 為壓電元件夾持電容，VDC為整流直流電壓，VOC，org 為原始開路電壓幅值，VD 為二極管壓降。

　　2.2 電感同步開關能量采集電路

　　傳統的經典能量采集電路由于電路一直處于通路狀態，電路本身損耗比較大，加之電路本身的結構缺陷，導致能量采集效率低下。為了解決這個問題，研究人員提出了一種基于電感的同步開關的能量采集電路SSHI（ Synchronized Switch Harvesting on Inductor），該電路包括一個電子控制開關，當壓電結構的位移達到最大值或最小值這個開關就被觸發，研究表明SSHI 電路的能量采集效率遠高于標準電路。該類電路又分為并聯同步開關電路（ P-SSHI）和串聯同步開關電路（S-SSHI）。

　　傳統的SSHI電路原理圖如圖3 所示，電路的大部分時間斷開的，這樣能量采集電路本身的損耗就比較小，可以很好的提高能量采集效率。開關只有在位移達到最大值或最小值時才閉合，此時組成一個L-Cp 振蕩回路，電路振蕩周期遠小于機械振蕩周期，每次開關閉合后，存儲在壓電片Cp 上的能量便通過整流橋和電感L 轉移到電容Cr上來。

　　圖3 傳統的SSHI電路原理圖

　　通過（1）可知等效電流ieq和速度成比例，這些開關動作可以保證Vp 和ieq是同相位的，所以從機械部分到電部分的輸入能量永遠是正的。Lefeuvre 等研究了SEH 電路和S-SSHI 電路的最大輸出功率：

　　式中，α 為力因子，ω 是振動角頻率，C0 是壓電元件夾持電容，UM 為壓電元件振動位移幅值，Qi 為SSHI電路品質因子。

　　通過上式可以看出S-SSHI 電路的最大輸出功率是SEH 電路的（1+e-π/2Qi ） / （1+e-π/2Qi ） 倍，顯然可以通過選擇合適的電路品質因子Qi 顯著的提高SSHI 電路的最大輸出功率。

　　3 自感知型電感同步開關能量采集電路

　　然而傳統的SSHI 電路的有一個致命的缺點：它不是一個自感知電路，即開關S 的通斷，需要位移傳感器和數字控制器，這些都需要額外的能量供給，有悖于能量采集研究的初衷。為此，本文根據文獻［12］給出的電子開關設計（ 如圖4），提出了一種自感知的同步開關能量采集SS-SSHI（Self-Sensing Synchronized Switch Harvesting on Inductor） 方法，僅依靠模擬電路就可以自動的根據壓電元件輸出電壓的變化控制開關的開閉。

　　圖4 電子開關

　　3.1 SS-SSHI電路工作原理

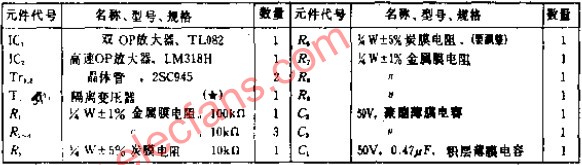
　　在自感知同步開關電路設計中，我們使用了互補的晶體管拓撲結構來實現對壓電片兩端電壓Vp 的直接包絡檢測：其中一部分用于最大值檢測，剩下的對稱部分用于最小值檢測。對SSHI 電路的改進電路SS-SSHI 如圖5 所示，圖中的主要元件的型號如表1。

　　圖5 SS-SSHI 電路原理圖

　　圖中Vp 為壓電陶瓷片兩端電壓，VC1 和VC2 分別為電容C1 和C2兩端電壓。和傳統的SSHI 電路一樣，在每個周期內，伴隨著振動位移的變化，電子開關會在電壓Vp 達到最大值時或者最小值時閉合。

　　圖6 SS-SSHI 電路電壓變化曲線

　　由于我們采用的是互補拓撲結構，所以電路中的最大值檢測和最小值檢測是對稱的。本文將重點討論最大值檢測原理（最小值檢測與此類似），結合電路工作的四個階段，給出SS-SSHI 電路的工作特性。對于最大值檢測，開關R1，D1 和C1 組成包絡檢測器，T1 作為比較器，而T3 作為電子開關。四個階段的電壓變化如圖7 所示。

　　自然充電階段：電路剛開始工作時，由于壓電元件的電壓是從0 開始增加的，所以要有一個自然充電階段。自然充電時的電流走向如圖8，電路導通部分為圖中藍線部分。在這個階段只有兩個包絡檢測器電路是導通的，而所有的三極管是斷開的。正向的等效電流ieq給Cp ，C1 和C2 充電，這樣Vp ，VC1和VC2也同時地增長。

　　ads/allimg/150806/1034164X2-10.JPG" width="411" />

　　圖7 電壓Vp 變化曲線

　　圖8 自然充電

　　第一次電壓翻轉階段：當Vp 達到它的最大值Vmax時，電容C1 兩端的電壓為Vmax -VD ，這里VD 為二極管上面的壓降。接著，Vp 開始下降，當下降值達到VD +VBE，也就是Vp = V1（ T1 時刻） 時，三極管T1 導通。電容C1 通過T1（ec） ，D3，T3（be） ，Crect，D8，Li 和r開始放電，結果使得T3 導通。由開關T3 導通產生的感應回路：D5，T3（ce） ，Crect，D8，Li 和r 使得Cp 兩端迅速短路。Cp 開始從電壓V1 通過感應回路迅速放電，直到Vp 達到其局部最小值（t2 時刻）。第一次電壓翻轉的電流走向如圖9 所示，電路導通部分為圖中粗實線部分。

　　圖9 第一次電壓翻轉

　　第二次電壓翻轉階段：通過Li 的電流開始翻轉其方向，但是T3（ce） 這條回路由于D5 的電流翻轉而立即阻塞。但由D7，Crect，T4（ce） 和D6 組成的回路還是可以導通的。因為即使T4 是斷開的，在它的發射極和集電極總存在一個小的沒有充電的寄生電容。翻轉電流就通過這條回路，直到T4 的發射極—集電極電容CCE 充滿電，此時（ T3 時刻），Vp 變為V3。Vp的局部最小值也就是V2 可能導致最小值開關的誤判。因此R2 是必須的，以確保用來最小值檢測的C2 的放電比Cp 慢， 這樣可以跳過局部最小值。圖10 顯示了第二次電壓翻轉的電流走向，電路導通部分用加粗實線表示。第二次電壓翻轉在自感知的能量采集電路中起副作用，可以選擇小的發射極—集電極電容CCE 可避免這種作用。然而，實際三極管中永遠存在寄生電容。

　　圖10 第二次電壓翻轉

　　電荷中和階段：在t3 時刻后，T3 和T4 都斷開了，但C2 仍舊沒有結束放電，C2 上剩余的電荷將流入Cp 和C1 直到他們擁有相同的電壓。這個電荷中和又導致Vp 在進入下半個周期即最小值檢測之前增大了一點至V4。C2 實際放電是從t1 時刻開始的，但是為了便于分析，假設電荷中和階段和其它3個階段一樣也是獨立的，電荷中和階段的電流走向如圖11，電路導通部分用粗實線表示。

　　圖11 電荷中和

　　最小值開關檢測可由電路中剩余的對稱部分完成，其原理和最大值檢測類似。只是對于最小值檢測，中間電壓就分別變為-V1，-V2，-V3 和-V4。

　　3.2 SS-SSHI 電路分析

　　3.2.1 開關相位延遲

　　根據文獻［7］中SSHI 電路的原理分析，開關動作應該剛好發生在電壓Vp 達到它的極值，也就是Vmax或Vmin。然而在SS-SSHI 電路中，開關動作剛好在這一時刻是不可能的，由于包絡檢測器和比較器里的二極管和三極管的壓降，所以在開關動作時刻和最大值（最小值） Vp 之間存在一個相位延遲。這個相位延遲可在圖6 中看出為ψ，可由下式計算得：

　　通過圖（6），可以看出開關動作時刻和位移最大值（也就是ieq =0）時刻之間的相位差φ 為：

　　其中θ 是壓電片電壓最大值Vp，oc 和ieq 的0 穿越點（從正到負）之間的相位差。顯然，這個相位差異φ是變化的，然而在文獻［15］ 中它被當成常數。

　　3.2.2 電路工作中的電壓變化

　　傳統的SSHI 電路，在半個振動周期內只存在兩個階段即自然充電和電壓翻轉階段，這兩個中間電壓可以通過這兩個過程中的充電和放電來計算。而在SS-SSHI 電路中，由于自感知開關電路中各階段的交互作用，更多的階段需要區分開來以便更好地分析電路的特性。四個階段的電路工作原理在前面已敘述過，從圖7 中可看出四個階段的電壓從V1 到V4 的變化。

　　對于最大值的開關檢測，如果V1 》Vref1，則Vp 開始進入第一次電壓翻轉。這里Vref1是參考電壓：

　　對于第一次電壓翻轉（從V1 變到V2），Cp ，C1，Li和r 組成了一個RLC 放電回路，它的品質因子為：

　　V2 和V1 的關系可表示為：

　　在第一次翻轉后，如果V2 《 Vref2，Vp 將又會翻轉。

　　對于第二次翻轉（ 從V2 到V3 ），Cp ，CCE，Li 和r串聯形成一個RLC 放電回路，它的品質因子為：

　　就可以得到V3 和V2 的關系：

　　假設C2 的放電是在電壓Vp 的兩次翻轉之后，電荷中和就可以被當成一個獨立的階段。在電荷中和階段，Cp ，C1 和C2 上的總電荷是要被放掉的。考慮到電荷守恒，則V4 和V1，V2，V3 的關系如下：

　　電荷中和結束后， 自然充電階段又開始了。在剩下的半個周期內，直到Vp 達到-V1，最小值開關開始工作。由于兩次翻轉和電荷中和階段的時間遠小于半個振動周期，所以Vp 的值可以近似為Vp，oc 在開關時刻的值，所以這個階段的電壓關系如下：

　　結合線性方程（9），（13），（15）和（16），可以得出V1到V4 關于VOC和VDC的解。

　　3.2.3 功率分析

　　根據（2） 和（3） 可以得出SS-SSHI 電路的能量采集功率為：

　　這里f0 =ω / 2π 是振動頻率。

　　由于精確計算V1，V2，V3，V4 的數值解較困難，所以采用等效法近似計算功率。考慮到電路第三階段和第四階段電壓的變化較小，即圖7 中V2 到V3，V3 到V4 變化相對于V1 到V2 的變化特別小，所以我們可以認為V2= V3 = V4，此時（17）可以近似為：

　　又由于Rp 的值一般都特別大，為數十兆或者更大，所以（16）可以近似為：

　　這樣結合式（9）和（19）就可以得出V1 和V2，帶入式（18）就可得出SS-SSHI 電路的能量采集功率。

　　4 實驗與結果分析

　　4.1 實驗系統與實驗方法

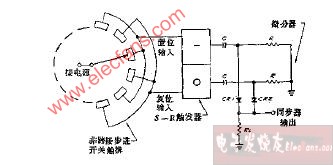
　　為了驗證SS-SSHI 電路的能量采集效果，我們設計了如圖12 所示的實驗系統。圖中器件分別為1. 函數信號發生器、2. 示波器、3. 激振器、4. 壓電陶瓷片、5. 激振器驅動電源、6. 能量采集電路。

　　圖12 能量采集系統

　　在實驗中首先由信號發生器產生諧波激勵信號，并輸入至激振器驅動電源，用以驅動激振器以某一頻率振動，繼而帶動安裝在激振器上的壓電懸臂梁振動，通過正壓電效應，把機械能轉化為電能，并依靠能量采集電路進行能量采集，最后通過示波器來觀察能量采集效果。

　　整個系統的主要參數如表2 所示。一般為了使采集的能量最大，都選擇在壓電體（懸臂梁） 的共振頻率處激振，此時壓電體（ 懸臂梁） 可產生更大形變，增大輸出功率。由于懸臂梁的固有模態比較高，為了降低諧振頻率，實驗中在懸臂梁的末端附加一個10gn 的質量塊（砝碼）。為了觀察諧振效果下的能量采集效率，本實驗選用了懸臂梁的一階模態頻率f =22.3 Hz 作為激勵源信號的頻率。

　　仿真電路圖5 中所示的電子元件的具體參數詳見表3，在實驗中我們通過選用不同阻值的電阻來模擬不同的負載，然后通過示波器分別觀察SS-SSHI 電路和SEH 電路在負載端輸出的電壓，這樣就可以根據前文所述的理論求得它們實際的能量輸出功率。

　　表

　　4.2 實驗結果分析

　　我們可以通過示波器觀察SS-SSHI 電路的工作狀態，其結果如圖13 所示，圖中給出了能量采集壓電片兩端電壓Vp 的變化曲線和信號發生器輸入的諧波激勵信號。結果表明SS-SSHI 電路實現了最大（最小）位移處的電壓翻轉，達到了設計預期。

　　圖13 SS-SSHI 電路工作電壓曲線

　　根據前述理論，盡可能提高電路的輸出功率是我們研究能量采集電路的主要目的。通過式（4） 和（20） 我們可以計算SEH 電路和SS-SSHI 電路的實際輸出功率。但在求SS-SSHI 電路功率時需要知道相位差φ。為了測得該參數，我們在懸臂梁正反兩面對稱粘貼兩片壓電片，其中一片用于能量采集，另一片則是作為傳感器，依靠其輸出電壓確定位移極值處所對應的時刻，通過對比兩片壓電片的波形就可以確定φ 值。通過實驗我們發現φ 值會隨著不同負載的變化發生細小的變化，符合文獻［13］ 中認為φ 是固定不變的假設。在本實驗中測得相位差異φ =2π / 11。由此，根據式（4）和（20），我們可以得到開路電壓幅值VOC，org = 10.3 V 時SS-SSHI 電路和SEH 電路的理論功率曲線如圖14 所示。

　　為了和理論結果進行比較，分別采用多個電阻進行實驗研究，不同的負載會導致電路輸出不同的直流電壓VDC ，根據阻值大小，由公式P =U2 / R 可計算實際輸出功率。圖14 表明，兩種電路的實測功率與理論分析結果相吻合，尤其是本文給出SS-SSHI電路的功率理論計算結果與實測值非常接近。

　　圖14 理論和實驗功率曲線

　　為了進一步對比不同振動水平下，采集電路輸出功率的提高幅度，本文還開展了開路電壓VOC，org =2.6 V 和VOC，org = 6.5 V 時的兩組實驗，結果如圖15所示。

　　圖15 不同開路電壓下的能量采集功率

　　由圖15 可知：在振動幅度較小時，壓電片兩端的開路電壓幅值VOC，org = 2.6 V（ 如圖15（ a）），此時SS-SSHI 電路在R = 50 kΩ 時功率達到最大， 即0.007 mW;而SEH 電路R = 180 kΩ 時功率達到最大，即0.008 mW。可知SS-SSHI 電路的能量采集效率和SEH 電路的能量采集效率相似。隨著振動幅度增大，開路輸出電壓亦增大，SS-SSHI 電路的優勢逐漸表現出來，在VOC，org = 6.5 V 時如圖15（ b），SSSSHI電路在R = 30 kΩ 時功率達到最大：0.110 4mW;而SEH 電路R =70 kΩ 時功率達到最大：0.083mW。此時SS-SSHI 比SEH 能量采集功率提高33%，而在VOC，org =10.3 V 時如圖15（c），SS-SSHI 電路在R = 30 kΩ 時功率達到最大：0.415 4 mW;而SEH 電路R =70 kΩ 時功率達到最大：0.208 5 mW。此時SS-SSHI 比SEH 能量采集功率提高99.23%。由此可見SS-SSHI 電路更適合高輸入電壓情況下的能量采集。

　　5 結論

　　微能源越來越受到人們的重視，而振動能作為最常見的能量存在形式受到人們的重視。壓電元件以其獨特的優勢使得它在振動能量采集方面得到廣泛應用。

　　本文首先對壓電振動能量采集系統進行電學模型等效建模，緊接著簡單分析了傳統的標準能量采集電路SEH 的工作原理和采集效率。簡要闡述了SSHI電路的工作原理并針對其開關控制需要額外功能的缺點設計并實現了一種自感知的能量采集電路SSSSHI。這種 SS-SSHI 電路不需要任何外界額外的能量供給就能實現開關的自行通斷，在振動位移（電壓）達到最大值或最小值時，開關打開使得壓電元件上的能量通過整流橋流入負載來達到能量采集的目的。通過理論分析和實驗驗證，這種SS-SSHI 電路能夠顯著地提高能量采集功率，在VOC，org = 10.3 V 時，SS-SSHI 比SEH 能量采集功率提高達99.23%。實驗同樣表明在大輸入電壓情況下SS-SSHI 電路的能量采集功率比SEH 電路的能量采集功率更能得到顯著的提高。