電子發燒友App
電壓源和電流源及電路基本器件R、C、L
????式中，E和R 值為常數，U和I的關系稱為電源的外特性，如圖1-9所示 。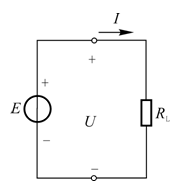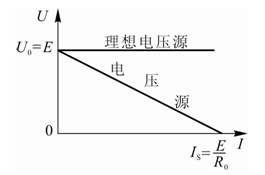
?????????????? 
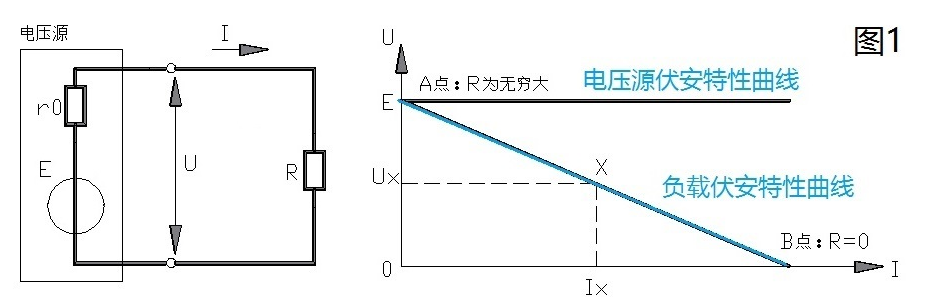
圖1-8 電壓源電路????????????????????????????? 圖1-9 電壓源和理想電壓源的外特性曲線????當I=0(即電壓源開路)時，U=Uo=E(開路電壓等于電源的電動勢)。
????當U=0(即電壓源短路)時，I=IS= (IS稱為短路電流)。
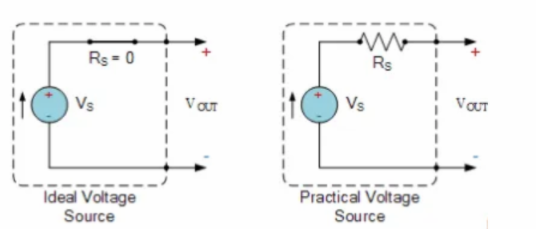
????當R=0時，電壓U恒等于電動勢E，是一定值，而其中的電流I則是任意值，由負載電阻R 及電壓U本身確定。這樣的電壓源稱為理想電壓源或恒壓源。理想電壓源如圖1-10所示。
????常見實際電源(如發電機、蓄電池等)的工作機理比較接近電壓源，其電路模型是E和R 的串聯組合。理想電壓源實際上是不存在的。但在電流源內阻R 遠小于負載電阻R ，內阻上的壓降IR 將遠小于U，則可認為U≈E，基本上恒定，這時可將此電壓源看成是理想電壓源。通常用的穩壓電源可認為是一個理想電壓源。
????如將式(1-3)兩端除以R ，得
???????????????????????????? ?
????
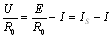
????當R=∞(相當于R支路斷開)時，電流I將恒等于IS，是一定值，而其兩端的電壓U則是任意值，由負載電阻RL及電流IS本身確定。這樣的電源稱為理想電流源或恒流源。理想電流源如圖1-13所示電工電子技術是面向高等工科院校非電專業學生的一門技術基礎課。
????理想電流源是不存在的，但是在電源內阻R 遠大于負載電阻R ，即R>>R 時，R 支路的分流作用很小，則可認為I≈IS基本恒定，這時可將此電流源看成是理想電流源。
????① 將如圖1-14所示左邊的電壓源等效變化為電流源時，電流源的電流 IS= (即電壓源的短路電流)。IS流出的方向與E的正極相對應，與IS并聯的內阻R 就等于與E串聯的內阻R ，等效變換所得的電流源如圖1-14(a)所示。
????② 將圖1-14右邊所示的電流源等效變換為電壓源時，電壓源的電動勢E=ISR (即電流源的開路電壓)，E的正極與IS流出的方向相對應；與E串聯的內阻R 就等于與IS并聯的內阻R ，等效變換所得的電壓源如圖1-14(b)左邊所示。
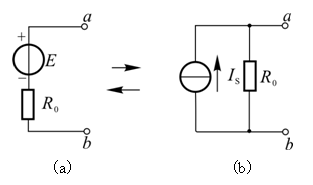
圖1-14?電壓源與電流源的等效變換????但是，電壓源和電流源的等效關系只是對外電路而言的，對電源內部是不等效的。例如圖1-14中，當電流源開路時，電源內部有損耗，IS流過R 產生損耗，而當電流源短路時，電源內部無損耗，R 無電流流過。而將其等效變換為圖1-14左邊所示的電壓源后，情況就不同了。當電壓源開路時，R 無電流通過，電源內部無損耗，而當電壓源短路時，R 中有電流IS= 流過，在電源內部產生損耗。
????理想電壓源和理想電流源之間沒有等效的關系。因為對理想電壓源(R =0)來講，其短路電流IS為無窮大，對理想電流源(R = ∞)講，其開路電路Uo為無窮大，都不能得到有限的數值，故這兩者之間不存在等效變換的條件。
????【例1-2】 求圖1-15(a)所示電路的電流I。
????解：圖1-15(a)的電路可簡化為圖1-15(d)所示的單回路電路，簡化過程如圖1-15 (b)、圖1-15(c)、圖1-15(d)所示，由簡化后的電路可求得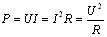
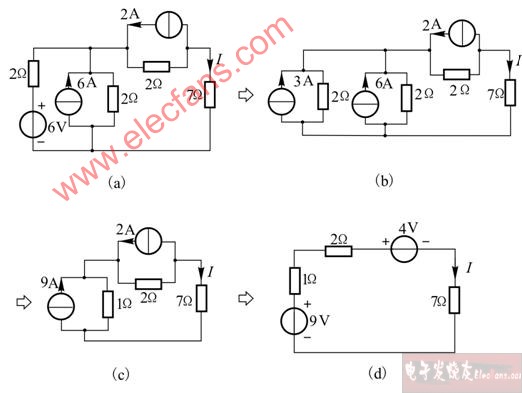
圖1-15 例1-2的圖
????電源是任何電路中都不可缺少的重要組成部分，它是電路中電能的來源。實際電源有電池、發電機、信號源等。電壓源和電流源是從實際電源抽象得到的電路模型。電路元件是電路中最基本的組成單元。電阻元件、電容元件、電感元件都是組成電路模型的理想元件。電阻、電容和電感這三個名詞即代表了三種理想的電路元件，又是表征它們量值大小的參數。
一、電壓源
????任何一個電源，都含有電動勢E和內阻R0。在分析與計算電路時，往往把它們分開，組成由E和R串聯的電源的電路模型，即電壓源。圖1-8中a、b左邊部分所示。圖中U為電源的端電壓，當接上負載電阻R形成回路后，電路中將有電流I流過，則電源的端電壓為： ???????????????????????????????????????????????????????????????????????????????????? U =E－R0 (1-3)一、電壓源
????式中，E和R 值為常數，U和I的關系稱為電源的外特性，如圖1-9所示 。
?????????????? 圖1-8 電壓源電路????????????????????????????? 圖1-9 電壓源和理想電壓源的外特性曲線
????當U=0(即電壓源短路)時，I=IS= (IS稱為短路電流)。
????當R=0時，電壓U恒等于電動勢E，是一定值，而其中的電流I則是任意值，由負載電阻R 及電壓U本身確定。這樣的電壓源稱為理想電壓源或恒壓源。理想電壓源如圖1-10所示。
圖1-10 理想電壓源電路
二、電流源
????電源除用電動勢E和內阻R 串聯的電路模型表示外，還可以用另一種電路并聯模型來表示。????如將式(1-3)兩端除以R ，得
???????????????????????????? ?
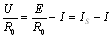
????即???????????????????????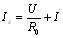 
????????????????????? （1-4）
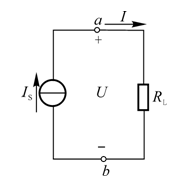
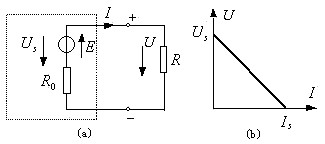
????這樣，我們就可以用一個電流源IS=和一個內阻R并聯的電路模型去表示一個電源，此即電流源。如圖1-11中a、b左邊部分所示，圖中U為電流源的端電壓，若接上負載電阻R構成回路后，其中將有電流I流過。
?????圖1-11? 電流源電路
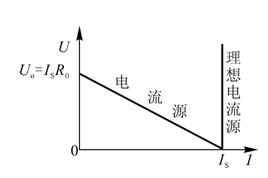
????式(1-4)中IS和R均為常數，U和I的關系稱為電流源的外特性，我們可以作出外特性圖，如圖1-12所示。當電流源開路時，I=0，U=UO=ISR；當其短路時，U=0，I=IS。內阻R越大，則直線越陡，R支路對Is的影響就越小。????當R=∞(相當于R支路斷開)時，電流I將恒等于IS，是一定值，而其兩端的電壓U則是任意值，由負載電阻RL及電流IS本身確定。這樣的電源稱為理想電流源或恒流源。理想電流源如圖1-13所示電工電子技術是面向高等工科院校非電專業學生的一門技術基礎課。
????
??
?? 圖1-12?電流源和理想電流源的外特性曲線???? ? 圖1-13?理想電流源電路
????通過本課程的學習使學生獲得電工與電子技術的基本理論、基本知識和基本技能。 像光電池一類的器件，工作時的特性比較接近電流源，其電路模型是電流源與電阻的并聯。????理想電流源是不存在的，但是在電源內阻R 遠大于負載電阻R ，即R>>R 時，R 支路的分流作用很小，則可認為I≈IS基本恒定，這時可將此電流源看成是理想電流源。
三、電壓源與電流源的等效轉換
????一個電源可用電壓源和電流源兩種電路模型來表示，且電壓源與電流源的外部特性相同。因此，電源的這兩種電路模型之間是相互等效的，可以進行等效轉換。兩者之間進行等效變化的方法如下。????① 將如圖1-14所示左邊的電壓源等效變化為電流源時，電流源的電流 IS= (即電壓源的短路電流)。IS流出的方向與E的正極相對應，與IS并聯的內阻R 就等于與E串聯的內阻R ，等效變換所得的電流源如圖1-14(a)所示。
????② 將圖1-14右邊所示的電流源等效變換為電壓源時，電壓源的電動勢E=ISR (即電流源的開路電壓)，E的正極與IS流出的方向相對應；與E串聯的內阻R 就等于與IS并聯的內阻R ，等效變換所得的電壓源如圖1-14(b)左邊所示。
圖1-14?電壓源與電流源的等效變換
????理想電壓源和理想電流源之間沒有等效的關系。因為對理想電壓源(R =0)來講，其短路電流IS為無窮大，對理想電流源(R = ∞)講，其開路電路Uo為無窮大，都不能得到有限的數值，故這兩者之間不存在等效變換的條件。
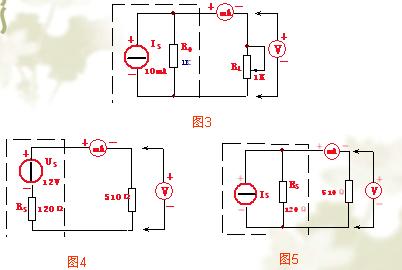
????【例1-2】 求圖1-15(a)所示電路的電流I。
????解：圖1-15(a)的電路可簡化為圖1-15(d)所示的單回路電路，簡化過程如圖1-15 (b)、圖1-15(c)、圖1-15(d)所示，由簡化后的電路可求得
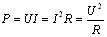
圖1-15 例1-2的圖
工商網監
評論