正弦交流電路的功率計算
如果一端口網絡的端口電壓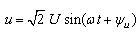
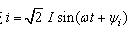 ,且電壓與電流參考方向一致,如圖3-9-1a所示。則由功率定義可得輸入該一端口網絡的瞬時功率為:
,且電壓與電流參考方向一致,如圖3-9-1a所示。則由功率定義可得輸入該一端口網絡的瞬時功率為:

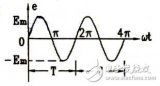
由式可看出,瞬時功率可分為恒定分量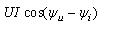 與二倍角頻率變化的正弦分量
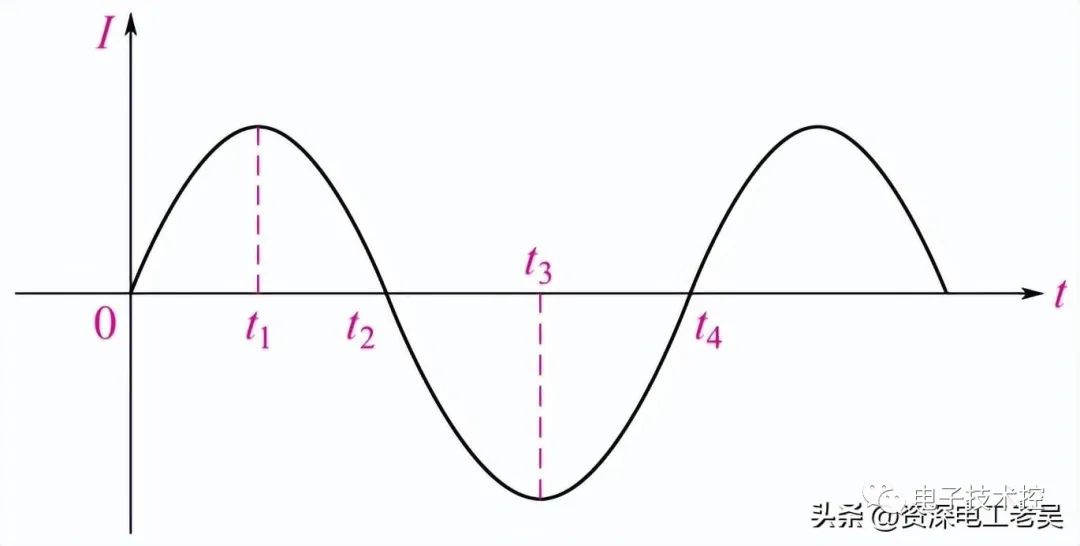
與二倍角頻率變化的正弦分量 。圖3-9-1b為端口電壓u、端口電流i與瞬時功率p的波形圖。瞬時功率在某些時間段為正值,表示此時一端口網絡正在吸收功率。在某些時間段為負值,表示網絡在輸出功率,將原來儲存的能量送回電網。
。圖3-9-1b為端口電壓u、端口電流i與瞬時功率p的波形圖。瞬時功率在某些時間段為正值,表示此時一端口網絡正在吸收功率。在某些時間段為負值,表示網絡在輸出功率,將原來儲存的能量送回電網。
在一周期內電路吸收的平均功率,也稱為有功功率。它的值為

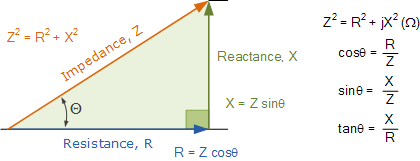
式中,U、I為負載端電壓和電流的有效值; 是端電壓與電流在關聯參考方向下的相位差;
是端電壓與電流在關聯參考方向下的相位差; 稱作功率因數角。由式可看出,決定一個一端口網絡負載平均功率的大小,不但與施加的電壓,流過的電流的有效值大小有關,而且與電壓電流的相位差,即功率因數角
稱作功率因數角。由式可看出,決定一個一端口網絡負載平均功率的大小,不但與施加的電壓,流過的電流的有效值大小有關,而且與電壓電流的相位差,即功率因數角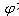 有關。當電壓電流相位差接近
有關。當電壓電流相位差接近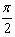 時,即使U與I的乘積很大,但負載所吸收的功率仍然很小,這是因為負載的功率因數
時,即使U與I的乘積很大,但負載所吸收的功率仍然很小,這是因為負載的功率因數 很小。例如對于純電感(或純電容)的負載,電壓與電流互相正交,
很小。例如對于純電感(或純電容)的負載,電壓與電流互相正交, ,
,![]()
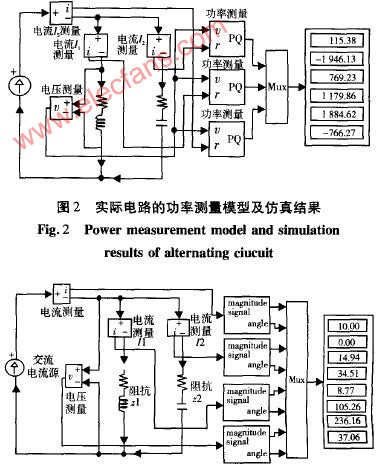
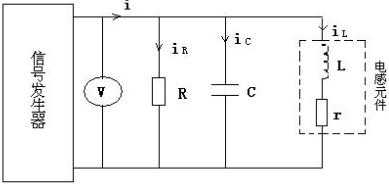
測量一端口網絡的功率時,電路連接如圖3-9-2b所示。將電流線圈串入被測量的電路,電壓線圈與端口并聯。二組線圈中分別流過電流,并產生磁場。功率表的讀數等于加在電壓線圈上的電壓有效值和通過電流線圈的電流有效值的乘積,再乘以電壓相量(參考方向從星號指向非星號)和電流相量(參考方
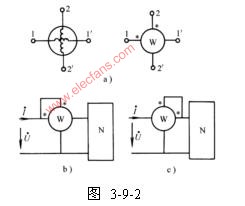
向也從星號指向非星號)之間的相位差的余弦,即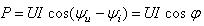 。若在測量同一負載功率時,功率表的連接方式改為如圖3-9-2c所示,此時流過電流線圈(參考方向為從非星號指向星號)的電流相量相位與原來接法相差180度,因此瓦特表的讀數為
。若在測量同一負載功率時,功率表的連接方式改為如圖3-9-2c所示,此時流過電流線圈(參考方向為從非星號指向星號)的電流相量相位與原來接法相差180度,因此瓦特表的讀數為 ,即讀數為負值。
,即讀數為負值。
有功功率、無功功率和視在功率的關系為

由上面各式可看出,視在功率、有功功率和無功功率組成一個直角三角形。
在電力系統的計算中,為了使功率計算表達方便,常在正弦電路中用復數功率來表示一個元件或一個單端口網絡的功率。復數功率定義為 的乘積,用符號
的乘積,用符號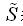 來表示,即:
來表示,即:
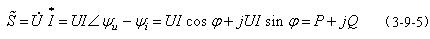
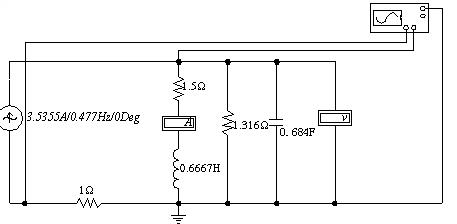
例3-9-1?? 圖3-9-3所示電路,已知 ,求輸入該電路的有功功率、無功功率和視在功率。
,求輸入該電路的有功功率、無功功率和視在功率。

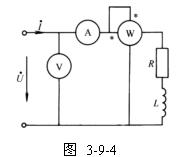
解:電感線圈可表示成電阻與電感的串聯電路,由已知測量數據可得電阻值為

 電子發燒友App
電子發燒友App








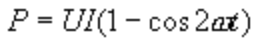
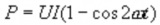


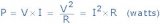
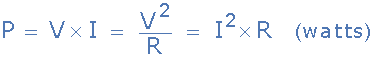
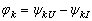
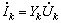
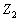
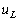












評論