?回路電流法?
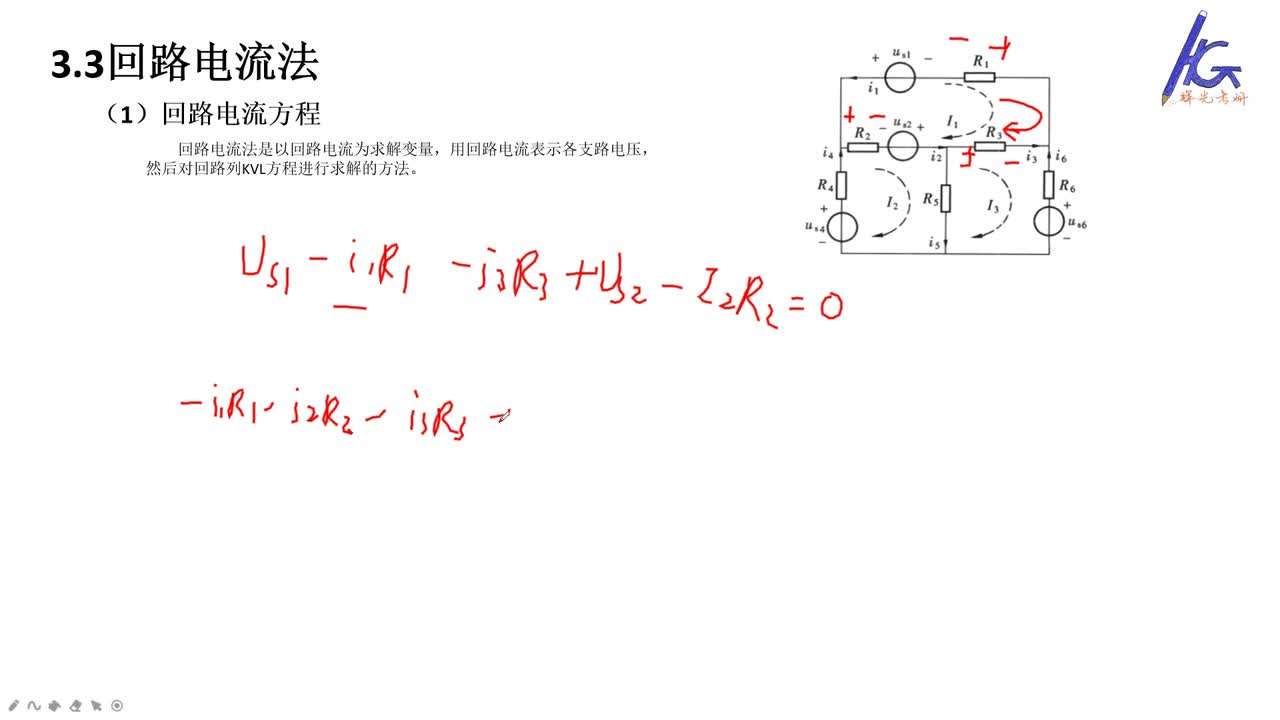
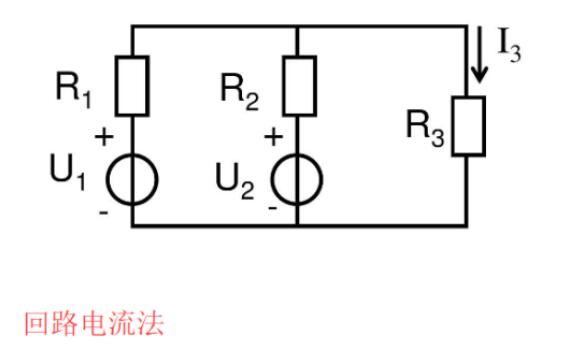
回路電流法是以一組獨立回路電流作為變量列寫電路方程求解電路變量的方法。倘若選擇基本回路作為獨立回路,則回路電流即是各連支電流。
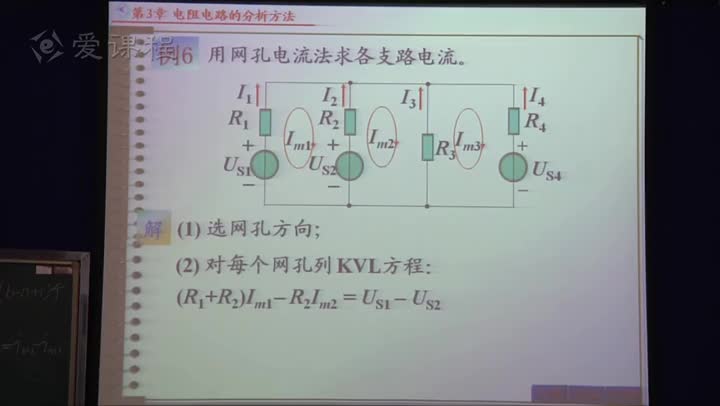
如圖2-3-1所示,已知![]() ,要求
,要求![]() 和
和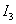 。這里仍然沿用介紹支路電流法的例題,現將運用回路電流法求解。首先選擇
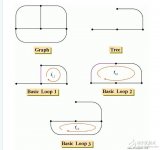
。這里仍然沿用介紹支路電流法的例題,現將運用回路電流法求解。首先選擇![]() 所在支路為樹支(用粗線條表示),如圖選擇各支路參考方程,以連支電流
所在支路為樹支(用粗線條表示),如圖選擇各支路參考方程,以連支電流![]() 作為變量,那么樹支電流就可以用連支電流表示,即:
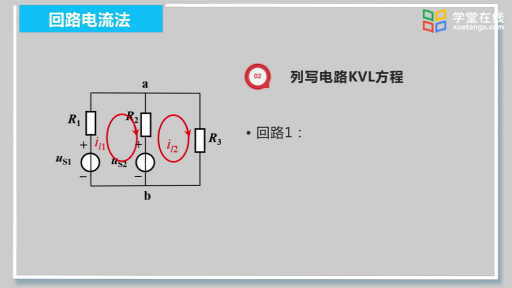
作為變量,那么樹支電流就可以用連支電流表示,即:![]() (式2-3-1),然后對兩個獨立回路列寫KVL方程,即:
(式2-3-1),然后對兩個獨立回路列寫KVL方程,即: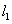
![]() (式2-3-2),
(式2-3-2),![]()
![]() (式2-3-3)
(式2-3-3)
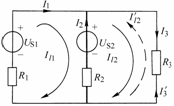
圖2-3-1
將(式2-3-1)代入(式2-3-2)與式(2-3-3),整理得到:
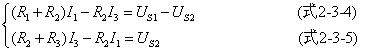
![]() ;
; ![]() ;
; ![]() 。
。
如果將圖2-3-1中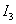 的參考方向反一下變為
的參考方向反一下變為 ,基本回路
,基本回路![]() 的取向也反一下為
的取向也反一下為![]() ,那么有:
,那么有:
![]()
 ?????? ?
?????? ?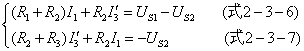
?
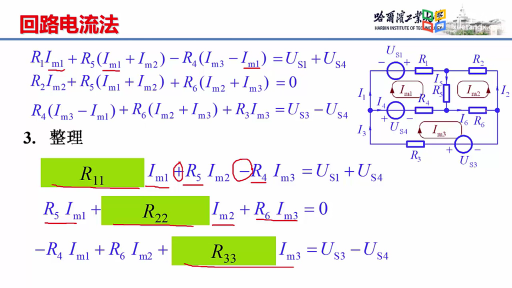
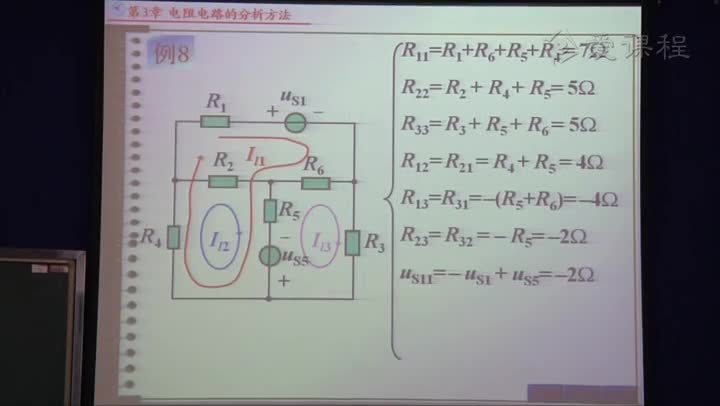
歸納(式2-3-4)—(式2-3-7),可以得到運用回路電流法列寫基本回路電流方程的一般式:

在(式2-3-8)(式2-3-9)中,![]() 稱為
稱為 回路的自電阻,等于
回路的自電阻,等于 回路中各電阻之和,恒為正;
回路中各電阻之和,恒為正;![]() 稱為
稱為 回路的自電阻,等于
回路的自電阻,等于 回路中各電阻之和,恒為正;
回路中各電阻之和,恒為正;![]() 稱為
稱為![]() 回路的互電阻,等于
回路的互電阻,等于![]() 兩個回路的公共支路電阻。當
兩個回路的公共支路電阻。當![]() 流經公共電阻時方向一致,互電阻為正,反之,互電阻為負。(式2-3-8)(式2-3-9)中方程的右邊是各個獨立回路中各電壓源電壓的代數和。當各電壓源電勢與回路方向一致時,相應電壓源電壓取正;反之,取負。
流經公共電阻時方向一致,互電阻為正,反之,互電阻為負。(式2-3-8)(式2-3-9)中方程的右邊是各個獨立回路中各電壓源電壓的代數和。當各電壓源電勢與回路方向一致時,相應電壓源電壓取正;反之,取負。
?????? 當電路中含有電流源、受控源時,其處理方法與支路電流法相同,請看例題。
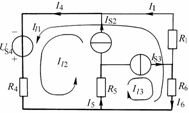
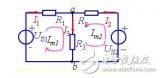
圖2-3-2? 例2-3-1附圖
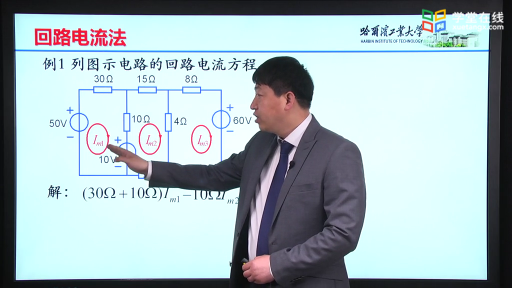
例2-3-1? 如圖2-3-2 所示電路中,已知:,![]() ,,
,,![]() ,,試用回路電流法求各支路電流。
,,試用回路電流法求各支路電流。
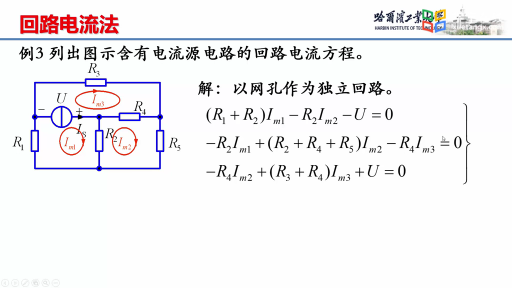
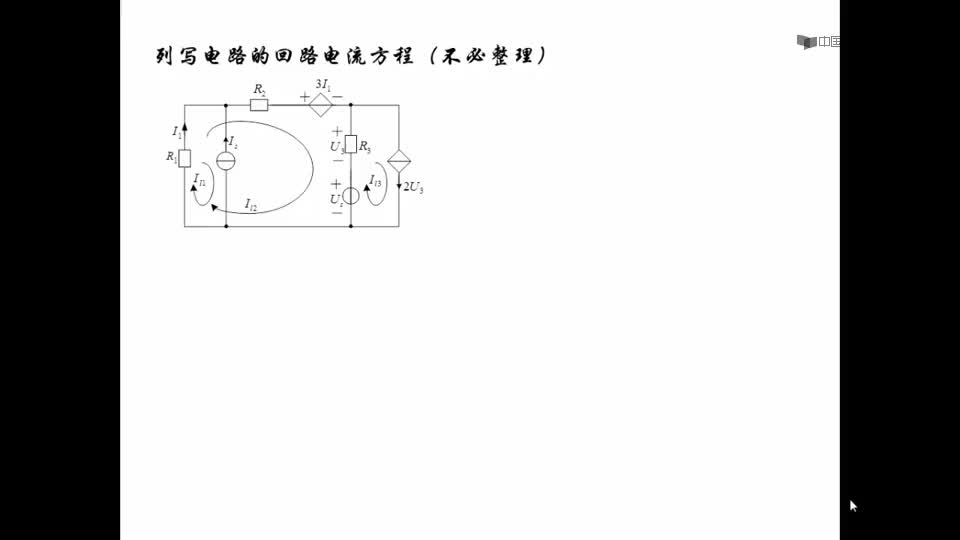
解:圖2-3-2中含有兩個電流源,電流源所在支路應盡可能放在連支上,因而選![]() 所在支路為樹(用粗線條表示),如圖選擇各支路電流參考方向,畫出3個基本回路,根據回路電流法,列出:
所在支路為樹(用粗線條表示),如圖選擇各支路電流參考方向,畫出3個基本回路,根據回路電流法,列出:
![]() ,
,![]() ,
, ![]()
代入已知數據得到:
例2-3-2??? 如圖2-3-3所示,已知:![]() 求各支路電流。
求各支路電流。
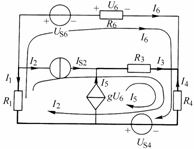
圖2-3-3? 例2-3-2附圖
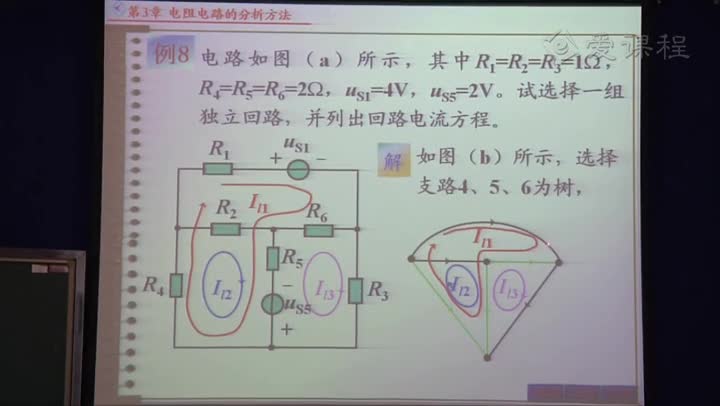
解:如圖選擇各支路電流參考方向,選擇![]() 所在支路為樹支(用粗線條表示),畫出三個基本回路,有:
所在支路為樹支(用粗線條表示),畫出三個基本回路,有:
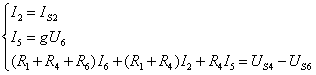
附加方程:![]() ,代入已知數據求解得到:
,代入已知數據求解得到:
![]()
 電子發燒友App
電子發燒友App















































































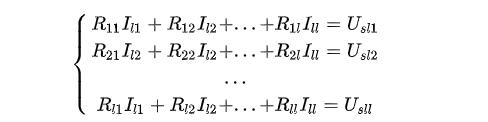











評論