傅里葉變換與拉普拉斯變換的聯(lián)系解讀 傅里葉變換和拉普拉斯變換都是數(shù)學(xué)中非常重要的分析工具。它們都在不同的領(lǐng)域中發(fā)揮著重要作用。 傅里葉變換是一種將時間域信號轉(zhuǎn)換成頻率域信號的技術(shù)。它是通過將信號
2023-09-07 17:04:19 219
219 如何用拉普拉斯變換分析電路 拉普拉斯變換是通過一種特定的方法將時域中的一個信號轉(zhuǎn)化為復(fù)頻域中的一個函數(shù),從而使得復(fù)雜的微分方程等可以變得更加簡單、易于求解。因此,它在電路分析中的應(yīng)用非常廣泛,有助于
2023-09-07 16:39:04 305
305 傅里葉變換拉普拉斯變換和z變換的區(qū)別聯(lián)系 傅里葉變換、拉普拉斯變換和z變換是信號處理中重要的數(shù)學(xué)工具。傅里葉變換用于將一個連續(xù)時間信號轉(zhuǎn)換為頻域表示;拉普拉斯變換則用于將一個連續(xù)時間信號轉(zhuǎn)換為復(fù)平面
2023-09-07 16:38:58 319
319 拉普拉斯變換公式? 拉普拉斯變換公式是數(shù)學(xué)中極其重要的一種變換方式,它的應(yīng)用領(lǐng)域非常廣泛,包括在信號處理、控制論、微分方程、電路分析和量子力學(xué)等領(lǐng)域中都有著廣泛的應(yīng)用。本文將詳細(xì)介紹拉普拉斯變換公式
2023-09-07 16:38:53 518
518 拉普拉斯變換的意義 拉普拉斯變換是微積分中的一種重要方法,用于將時間域函數(shù)轉(zhuǎn)換為復(fù)平面的頻域函數(shù)。它是工程和科學(xué)中常用的一種數(shù)學(xué)工具,尤其是電路理論、信號處理和控制理論中。 拉普拉斯變換的意義可以
2023-09-07 16:35:08 940
940 傅里葉變換和拉普拉斯變換的區(qū)別聯(lián)系 傅里葉變換和拉普拉斯變換是數(shù)學(xué)中兩種具有重要意義的變換方式。它們都在信號處理、傳輸和控制領(lǐng)域被廣泛應(yīng)用,能夠?qū)r域信號轉(zhuǎn)換為頻域信號或復(fù)平面上的信號。 傅里葉變換
2023-09-07 16:29:45 424
424 拉普拉斯變換的頻移特性 拉普拉斯變換是一種重要的數(shù)學(xué)工具,在信號處理、控制理論、電路分析等領(lǐng)域廣泛應(yīng)用。在這些應(yīng)用中,頻移是一個常見的操作,即將信號在頻域上移動某個頻率。 拉普拉斯變換是一種復(fù)數(shù)變換
2023-09-07 16:29:43 141
141 所以對于高階系統(tǒng),一般采用積分變換法,將時域函數(shù)變?yōu)轭l域函數(shù),從而將時域微分方程轉(zhuǎn)為頻域代數(shù)方程求解,求出頻域解后在還原為時域解。拉普拉斯變換是一種重要的積分變換。
2023-03-02 14:19:27 591
591 
傅里葉變化只能對能量有限的信號進(jìn)行變換(也就是可以收斂的信號),無法對能量無限的信號進(jìn)行變換(無法收斂),因此,拉普拉斯應(yīng)運(yùn)而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進(jìn)行時頻變換。
2022-11-28 11:00:23 1013
1013 關(guān)于拉普拉斯定義和基本性質(zhì)分析
2022-09-26 16:12:19 879
879 拉普拉斯變換表下載
2021-12-30 09:47:12 4
4 從傅里葉級數(shù)、傅里葉變換推出拉普拉斯變換。
2021-06-23 16:25:27 5437
5437 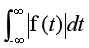
連續(xù)時間LTI系統(tǒng)狀態(tài)方程的求解第一項對應(yīng)系統(tǒng)狀態(tài)變量的零輸入解,第二項對應(yīng)系統(tǒng)狀態(tài)變量的零狀態(tài)解部分求拉普拉斯反變換就得到狀態(tài)變量的時間表達(dá)式第一項對應(yīng)系統(tǒng)的零輸入響應(yīng),第二項對應(yīng)系統(tǒng)的零狀態(tài)響應(yīng)求拉普拉斯反變換就得到系統(tǒng)的完全響應(yīng) [hide] [/hide]
2009-09-10 12:05:50
電子發(fā)燒友網(wǎng)為你提供通俗的角度看待拉普拉斯變換資料下載的電子資料下載,更有其他相關(guān)的電路圖、源代碼、課件教程、中文資料、英文資料、參考設(shè)計、用戶指南、解決方案等資料,希望可以幫助到廣大的電子工程師們。
2021-03-30 08:47:41 6
6 在知乎上看到一個問題,傅里葉變換、拉普拉斯變換、Z 變換的聯(lián)系是什么?為什么要進(jìn)行這些變換?我覺得這是一個非常好的問題,貌似一下子也回答不上來,所以整理學(xué)習(xí)并分享一下。
2021-02-15 11:59:00 7844
7844 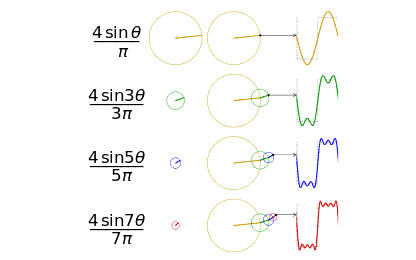
本文檔的主要內(nèi)容詳細(xì)介紹的是如何實現(xiàn)多聚焦圖像融合的拉普拉斯金字塔方法。
2021-02-03 11:40:00 2
2 本文檔的主要內(nèi)容詳細(xì)介紹的是拉普拉斯變換的習(xí)題與詳解免費下載。
2020-09-28 08:00:00 0
0 本文檔的主要內(nèi)容詳細(xì)介紹的是控制系統(tǒng)的數(shù)學(xué)模型拉普拉斯變換的詳細(xì)資料說明。
2020-06-09 08:00:00 0
0 本文檔的主要內(nèi)容詳細(xì)介紹的是拉普拉斯變換電路理論練習(xí)題來做作看吧。
2018-11-27 08:00:00 15
15 拉普拉斯變換是工程數(shù)學(xué)中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有引數(shù)實數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個引數(shù)為復(fù)數(shù)s的函數(shù)。
2018-09-17 08:02:00 11315
11315 
作為典型的具有熱存儲特性負(fù)荷,溫控負(fù)荷具有參與電力系統(tǒng)有功調(diào)度與控制的潛能。為了便于分析和控制,提出了一種溫控負(fù)荷群Fokker-Planck方程聚合模型的數(shù)值拉普拉斯反變換求解方法。分別介紹了溫控
2018-03-06 17:49:40 0
0 傅里葉變換與拉普拉斯變換的物理解釋及區(qū)別pdf文檔資料下載
2017-12-19 17:22:52 4
4 拉普拉斯變換是工程數(shù)學(xué)中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數(shù)實數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個參數(shù)為復(fù)數(shù)s的函數(shù)。拉普拉斯變換在許多工程技術(shù)和科學(xué)研究領(lǐng)域
2017-12-06 17:22:46 76342
76342 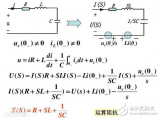
一種積分變換,它來源于函數(shù)的傅里葉積分表示。積分稱為? 的傅里葉積分。拉普拉斯變換是工程數(shù)學(xué)中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數(shù)實數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個參數(shù)為復(fù)數(shù)s的函數(shù)。
2017-12-05 19:10:02 83345
83345 
有些情形下一個實變量函數(shù)在實數(shù)域中進(jìn)行一些運(yùn)算并不容易,但若將實變量函數(shù)作拉普拉斯變換,并在復(fù)數(shù)域中作各種運(yùn)算,再將運(yùn)算結(jié)果作拉普拉斯反變換來求得實數(shù)域中的相應(yīng)結(jié)果,在經(jīng)典控制理論中,對控制系統(tǒng)的分析和綜合,都是建立在拉普拉斯變換的基礎(chǔ)上的。
2017-12-05 18:30:31 234698
234698 
關(guān)于利用拉普拉斯變換求解系統(tǒng)初值問題書中只給出了一種比較簡單的情況,即時域函數(shù)在零時刻有界時的求解方法。很遺憾,對于在零時刻存在沖擊情況下的初值問題,這種方法并不適用。而這種問題又是大量存在的,所以
2017-11-16 11:02:22 5
5 自動化基礎(chǔ)知識--拉普拉斯變換的概念
2017-10-26 08:53:36 1
1 基于CUDA的拉普拉斯金字塔的優(yōu)化_邵靖凱
2017-03-01 21:57:14 1
1 拉普拉斯變換及其應(yīng)用拉普拉斯變換及其應(yīng)用拉普拉斯變換及其應(yīng)用拉普拉斯變換及其應(yīng)用
2015-10-28 11:19:28 26
26 該文提出了一種基于拉普拉斯算法的圖像銳化方法,并在DSP上實現(xiàn)其算法。首先研究拄普拉斯算子銳化圖像的基本原理,并推導(dǎo)出圖像銳化的拉普拉斯算子。其次,根據(jù)拉普拉斯算子.
2011-10-12 16:22:55 79
79 應(yīng)用拉普拉斯變換分析RLC電路:應(yīng)用拉普拉斯變換分析R上c 電路,不需要確定積分常數(shù),從而避免了時域求解微分方程確定積分常數(shù)的繁瑣計算。關(guān)鍵詞:拉普拉斯變換;RLC電路
2010-04-12 08:31:44 124
124 z變換與拉普拉斯變換的關(guān)系:一.z平面與s平面的映射關(guān)系二.z變換與拉式變換表達(dá)式之對應(yīng)
2009-09-30 19:40:36 46
46 拉普拉斯變換視頻教程免費下載:一 拉普拉斯變換的定義 1、從絕對可積條件討論傅氏變換的問題,引入衰減因子的概念; 2、導(dǎo)出拉氏變換與逆變換公式; 3、單邊拉氏變換的概念;
2009-09-03 12:00:40 226
226 應(yīng)用拉普拉斯變換分析線性動態(tài)電路
圖9-5-1(a)所示是一個RLC串聯(lián)電路,初始條件是
2009-07-27 11:47:14 3482
3482 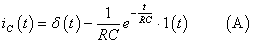
拉普拉斯變換的基本定理
本節(jié)介紹拉普拉斯變換(也稱為拉氏變換)的基本性質(zhì),了解掌握了這些性質(zhì),可以更加方便地求解各種拉普
2009-07-27 11:43:12 22114
22114 拉普拉斯變換
在電路分析中,如果將換路時刻作為時間的起點,那么我們只需研究
2009-07-27 11:42:43 4799
4799 拉普拉斯變換教案:§13-1 拉普拉斯變換的定義§13-2 拉普拉斯變換的基本性質(zhì)§13-3 拉普拉斯反變換的部分分式展開§13-4 運(yùn)算電路§13-5 應(yīng)用拉普拉斯變換法分析線性電路
2009-07-09 11:37:56 71
71 拉普拉斯變換及其應(yīng)用:1.1基本要求1,熟悉拉氏變換的基本法則2,熟練掌握典型函數(shù)的拉氏變換式。3,掌握用拉氏變換求解微分方程初值問題的思路。4,熟練掌握求有理分式
2009-07-08 11:43:00 128
128 什么是拉普拉斯變換
拉普拉斯變換:拉普拉斯變換(英文:Laplace Transform),是工程數(shù)學(xué)中常用的一種積分變換。如果定義: f(t),是一個關(guān)于t,的函數(shù),使得當(dāng)t<0
2009-07-08 11:42:30 4963
4963 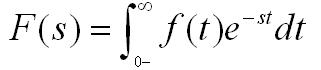
拉普拉斯變換公式
1、拉氏變換定義
2009-07-08 11:36:57 12239
12239 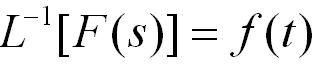
動態(tài)電路的復(fù)頻域分析 6.1 拉普拉斯變換及其性質(zhì) 6.2 拉普拉斯反變換 6.3 電路基本定律及電路元件的復(fù)頻域形式 6.4 應(yīng)用拉普拉斯變換分
2008-12-04 17:55:29 40
40
![]() 代入式中進(jìn)行積分,即可求出相應(yīng)的原函數(shù)
代入式中進(jìn)行積分,即可求出相應(yīng)的原函數(shù)![]() ,但往往求積分的運(yùn)算并不簡單。下面介紹求反變換的一種校為簡便的方法。
,但往往求積分的運(yùn)算并不簡單。下面介紹求反變換的一種校為簡便的方法。![]()
![]() 可通過多項式除法得:
可通過多項式除法得:![]()
![]() 的拉普拉斯反變換為:
的拉普拉斯反變換為:![]()
![]() 是有理真分式,記為。對于電路問題,多數(shù)F(S)是有理真分式即n≥m情況。為求
是有理真分式,記為。對于電路問題,多數(shù)F(S)是有理真分式即n≥m情況。為求![]() 的拉普拉斯反變換,通常利用部分分式展開的方法,將之展開成簡單分式之和。簡單分式的反變換,可直接查表9-1-1直接獲得。
的拉普拉斯反變換,通常利用部分分式展開的方法,將之展開成簡單分式之和。簡單分式的反變換,可直接查表9-1-1直接獲得。![]() ,求出相應(yīng)的幾個根,記作
,求出相應(yīng)的幾個根,記作![]() 。根據(jù)所求根的不同類型,下面分三種情況進(jìn)行討論。
。根據(jù)所求根的不同類型,下面分三種情況進(jìn)行討論。![]() 有幾個不相同的實數(shù)根時
有幾個不相同的實數(shù)根時![]() 按部分分式展開為:
按部分分式展開為:![]()
![]() ,
,![]() ,……
,……![]() 是對應(yīng)于
是對應(yīng)于![]() 極點
極點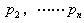 的留數(shù)。留數(shù)
的留數(shù)。留數(shù)![]() 可由下面兩式求出,即:
可由下面兩式求出,即:![]() ????? (式9-3-1)
????? (式9-3-1) ??(式9-3-2)
??(式9-3-2)![]() 的反變換式為:
的反變換式為:![]() ??? ???(式9-3-3)
??? ???(式9-3-3)![]() 的拉普拉斯反變換式。
的拉普拉斯反變換式。![]() 的部分分式展開式為:
的部分分式展開式為:
![]() ,
,![]()
![]()
![]() 包含有共軛復(fù)根時
包含有共軛復(fù)根時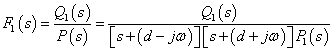
![]()
![]() 是實系數(shù)多項式時,
是實系數(shù)多項式時,![]() 是復(fù)數(shù),
是復(fù)數(shù),![]() 是
是![]() 的共軛復(fù)數(shù)。
的共軛復(fù)數(shù)。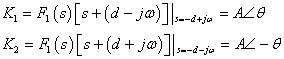
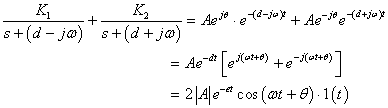
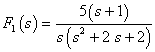 的原函數(shù)
的原函數(shù)![]() 。
。![]()
![]()

![]() 的原函數(shù)
的原函數(shù)![]() 為:
為:![]()
 電子發(fā)燒友App
電子發(fā)燒友App



































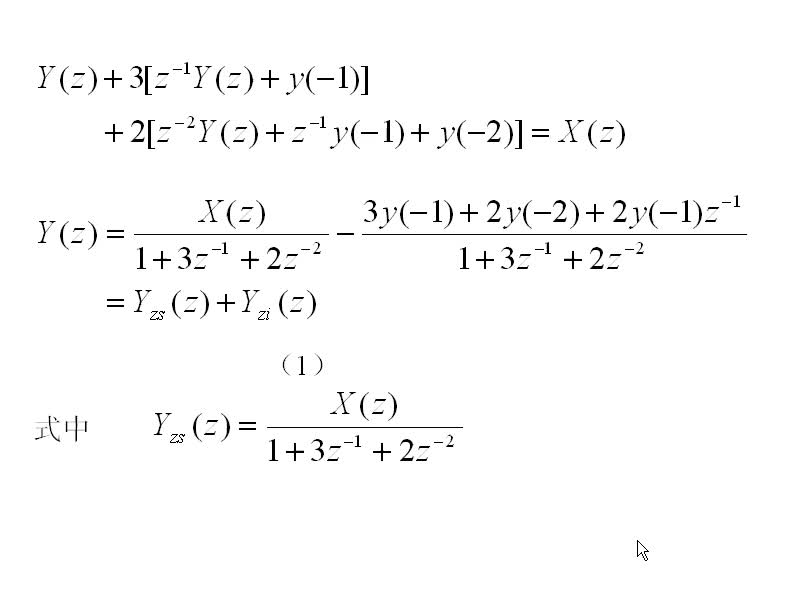













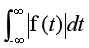





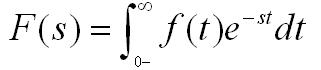
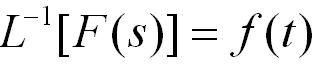










評論