分段線性化法是將特性曲線分為若干段,每段用直線近似,這樣每段中的伏安特性用直線方程表示或用等值線性電路表示,使分析計算大為簡化。分段線性化法的分析與計算可分為兩種方法:①折線方程;②等值電路法。??????
一、????????????? 折線方程法
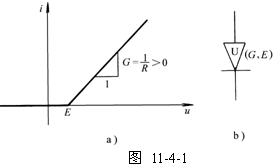
回憶圖11-2-2a電路,如二極管VD是理想的,總伏安特性如圖11-2-2d所示。將曲線的u、i軸互換,特性如圖11-4-1a所示,稱為凹形電阻特性,用圖11-4-1b表示其符號(圖11-2-4c的特性是凸形電阻特性)。
圖11-4-1a的電流可表示為:
![]() ??? (11-4-1)
??? (11-4-1)
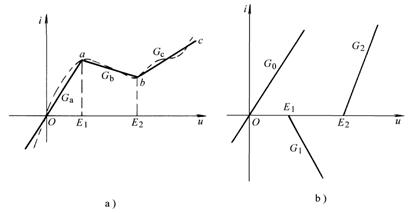
圖 11-4-2
圖11-4-2a虛線所示的電阻特性曲線可由三段直線Oa、ab、bc近似表示,這三段直線又可用圖11-4-2b中的一個線性電阻G0和兩個凹形電阻![]() 、
、![]() 的曲線相加而成。?????? 對于
的曲線相加而成。?????? 對于![]() :電導
:電導![]()
對于![]() :電導
:電導![]() (Gb為負,G1也為負)
(Gb為負,G1也為負)
對于![]() ;電導
;電導![]() ?? ?(11-4-2)
?? ?(11-4-2)
已知![]() 、
、![]() 、Gc(從圖11-4-2a中得到),聯立求解以上三式得:
、Gc(從圖11-4-2a中得到),聯立求解以上三式得:
![]() ??? ?(11-4-3)
??? ?(11-4-3)
于是:
![]() ??(11-4-4)
??(11-4-4)
整理得:
![]() ??(11-4-5)
??(11-4-5)
式中:???
![]()
![]()
![]()
![]() ??(11-4-6)
??(11-4-6)
式(11-4-5)稱為規范化分段線性方程。
例11-4-1? 圖11-4-3a所示電路,電源的電動勢![]() ,內阻
,內阻![]() ,與隧道二極管T連接,后者的特性可用三段近似直線表示(圖11-4-3b),求工作點。
,與隧道二極管T連接,后者的特性可用三段近似直線表示(圖11-4-3b),求工作點。
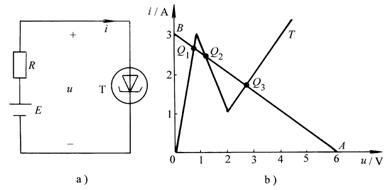
圖 11-4-3
解:對照式(11-4-5)、(11-4-6)可知:
![]() ;
;
從式(11-4-3)得:
![]()
從式(11-4-6)得:
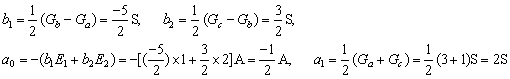
將各數據代入式(11-4-5),得到規范化分段線性方程:
![]() ??(11-4-7)
??(11-4-7)
為求電路中的電流i和電壓u,再列出電源的外特性方程:
![]() ? ?(11-4-8)
? ?(11-4-8)
現用解析法求解,即聯立求解式(11-4-7)和式(11-4-8)。當![]() 時,式(11-4-7)成為:
時,式(11-4-7)成為:
![]() ? ?(11-4-9)
? ?(11-4-9)
聯解式(11-4-8)、式(11-4-9)得:
![]()
當![]() 時,式(11-4-7)成為:
時,式(11-4-7)成為:
![]() ??(11-4-10)
??(11-4-10)
聯解式(11-4-8)、式(11-4-10)得:
![]()
當時,式(11-4-7)成為:
??(11-4-11)
聯解式(11-4-8)、式(11-4-11)得:
???
二、等效電路法
等效電路法是將給定的非線性曲線用線性電阻、直流電源和理想二極管組成的等效電路表示,這樣,非線性電阻電路化為含理想二極管的等效準線性電阻電路,便于分析計算。
圖11-4-2a的非線性電阻特性曲線用折線表示后,等值電路如圖11-4-4所示。
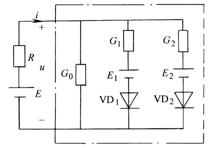
圖 11-4-4
現用等效電路法重新計算例11-4-1中隧道二極管的電壓和電流。利用該題數據:E=6V,R=2W,E1=1V,E2=2V,G0=3S,G1= -5S,G2=3S。
當時,二極管VD1、VD2斷開,電路成為E、R、G串聯,此時:

![]()
當時,VD1導通、VD2斷開,利用節點電壓法:
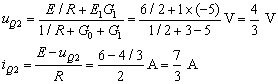
當時,VD1、VD2都導通,利用節點電壓法:
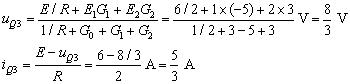
 電子發燒友App
電子發燒友App























評論