用定點小數引出數值的三種編碼(原碼、補碼和反碼)方法是最方便的。
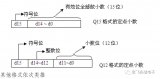
(1) 原碼表示法,是用機器數的最高一位代表符號,以下各位給出數值絕對值的表示方法。其定義為:
[X]原=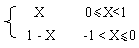 (2.9)
(2.9)
例如, X=+0.1011, [X]原=01011
X=-0.1011, [X]原=11011
按定義,當X=-0.1011時,[X]原= 1-X= 1.0000-(-0.1011) =11011。這里的X為數的實際值,即相應機器數的真值,[X]原為原碼表示的機器數。
原碼的性質:
① 在原碼表示中,機器數的最高位是符號位,0代表正號,1代表負號,以下各位是數的絕對值,即[X]原 = 符號位 + |X|。
② 在原碼表示中,零有兩種表示形式,即
[+0.0]原=00000, [-0.0]原=10000
設X、Y的真值分別為X=+0.0000,Y=-0.0000。則按原碼定義[X]原=00000, [Y]原= 1-Y = 1+0.0000 = 10000,因此零有原碼兩種表示形式。
③ 原碼表示方法的優點,是在數的真值和它的原碼表示之間的對應關系簡單,相互轉換容易,用原碼實現乘除運算的規則簡單。缺點是用原碼實現加減運算很不方便。要比較參與加減運算兩個數的符號,要比較兩個數的絕對值的大小,還要確定運算結果的正確的符號等,因此在計算機中經常用后面介紹的補碼實現加減運算。
(2) 補碼表示法,是用機器數的最高一位代表符號,以下各位給出數值按2取模結果的表示方法,其定義為
[X]補=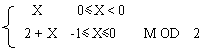 (2.10)
(2.10)
例如:
X=+0.1011, [X]補=01011
X=-0.1011, [X]補=10101
按補碼的定義,當X=-0.1011時,[X]補 = 2+X =10.0000+(-0.1011) = 10101。
補碼的性質:
① 在補碼表示中,機器數的最高一位是符號位,0代表正號,1代表負號。機器數和它的真值的關系,是 [X]補 = 2*符號位 + X。
② 在補碼表示中,0有唯一的編碼,即 [+0.0]補 = [-0.0]補 = 00000
假定X = +0.0000, Y = -0.0000,依據補碼定義, 則有
[X]補 = X = 00000, [Y]補= 2+Y = 10.0000+0.0000 = 10.0000 = 00000
此處最后一步實現按2取模,處在小數點左側第二位上的1去掉了。
③ 補碼表示的兩個數在進行加法運算時,可以把符號位與數值位同等處理,只要結果不超出機器能表示的數值范圍,運算后的結果按2取模后,得到的新結果就是本次加法運算的結果,即機器數的符號位與數值位都是正確的補碼表示,即:
[X+Y]補 = [X]補 + [Y]補 MOD 2 (2.11)
這一結論極為重要。
例如, X =+0.1010, Y = -0.0101,則:
[X]補= 01010, [Y]補= 11011,求得:
[X]補 + [Y]補 = 01010+11011 = 100101 ,按2取模后,符號位前邊一位上的1去掉,則最后結果為00101,其真值為 +0.0101。符號位與數值位均正確。
又如,X1=X2=-0.1000,則[X1]補=[X2]補 =11000 那么[X+X]補=11000+11000=110000,按2取模后得10000,它的真值為-1。由此看出,用補碼表示定點小數時,它能表示-1的值。
④ [X]補與其真值的關系。假定[X]補= X0X1X2…Xn,則有[X]補= 2X0+X,此關系對X為正、為零和為負都是正確的。X為正時,X0應為0,[X]補= 2*0 + X = X,X為負時,X0應為1,[X]補 = 2*1+X = 2 + X ,均與補碼的定義吻合。由此又可以得到從[X]補求X的關系,即由機器數求其代表的真值的關系如下:
X = [X]補 - 2X0
= X0X1X2…Xn - 2X0
= -X0 + 0.X1X2…Xn (2.12)
當X為正數時,X0=0 真值 X = [X]補 ;
當X為負數時,X0=1 真值 X = -1 + 0.X1X2…Xn = -(1-0.X1X2…Xn)。
對補碼的數值部分求補,并加上符號即得真值。
例如[X補=10110,則X的真值 = -(1-0.0110) = -0.1010。當已知補碼而需求此數的真值時可采用此法,此公式在推導補碼乘法的運算算法中很有用。
⑤ 補碼的算術移位
將[X] 補的符號位與數值位一起右移一次并保持原符號位的值不變,可實現除法功能(除以2),即[X/2]補= X0X0X1X2…Xn-1Xn。今考慮X為正、負數兩種情況。
設: X= 0.0110, [X]補=00110,右移一位得00011,是X除以2的補碼結果。
設: X=-0.0110,[X]補=11010,計算 [X/2]補=11101,再按④求真值得X/2=-0.0011,說明得到的確實是X除以2的結果。
為了得到一個數的補碼表示,當然可以通過補碼的定義求得,但更簡便的辦法是:
當X≥0時,[X]補的符號位取0,數值位取X的各數值位上的值,此時有[X] 補=[X] 原。
當X<0時,[X]補的符號位取1,將X的各數值位取反(0變1,1變0)再在最低位加1,以得到 [X]補的各數值位上的值。
從[X]原求 [X] 補時,對正數或零,有[X] 補=[X]原,對負數,是符號位不變,各數值位變反后再在最低位執行加1操作。同理,由[X]補求 [X]原時,對負數仍是符號位不變,各數值位變反后再在最低位執行加1操作。
在說明補碼的性質(3)時,特別強調兩個數的補碼相加,僅在其運算結果不超出機器能表示的數值范圍時,運算結果才是正確的,否則得到的結果不正確。如[X]補+[Y]補=01001+01010=10011。兩個大于0.5的正數相加,結果的符號位變成負號,數值部分也是錯誤的。這是因此參加運算的兩個數的和大于1,超出了機器所能表示的范圍,產生了所謂的 "溢出"。對負數也會產生溢出,如[X]補+[Y]補=10101+10100=01001,兩個負數相加,結果的符號位卻變成正號,說明結果是錯誤的。
為了方便判別結果是否溢出,某些機器采用變形補碼,又稱模4補碼表示方法,其定義為:
[X]補= (2.13)
(2.13)
也就是常說的雙符號位的補碼表示。例如:
X=+0.1011, [X]補=001011
X=-0.1011, [X]補=110101
按模4補碼定義,當X=-0.1011時,[X]補= 4+X = 100.0000+(-0.1011) = 110101。從上式的結果可以看出,模4補碼的表示就是在模2補碼表示的符號位之前再增加與原符號同值的另一個符號位。
模4補碼的性質:
① 模4補碼的兩個符號位相同,00表示正號,11表示負號,其數值位與其模2補碼相同。當符號位為01或10時,表示數值溢出。01表示兩個正數相加之和≥1的情況,通稱數值 "上溢";為10時,表示兩個負數相加,而其和小于-1的情況,通稱數值 "下溢"。前面的1個符號位是正確的符號位。
② 在模4補碼表示中,零有唯一的編碼,即 [+0.0]補 = [-0.0]補= 000000。模4補碼能表示-1,即為110000,與模2補碼的情況非常類似。
模4補碼具有模2補碼的全部優點,而且更容易檢查加減運算中的溢出情況。有必要指出,存儲每個模4的補碼數時,只要存一個符號位,因為任何一個正確的數值,其模4補碼的兩個符號位總是相同的。只在把兩個模4補碼的數送往算術與邏輯運算部件完成加減計算時,才把每個數的符號位的值同時送到算術與邏輯運算部件的兩位符號位,即只在算術與邏輯運算部件中采用雙符號位。
3) 反碼表示法,是用機器數的最高一位代表符號,數值位是對負數值各位取反的表示方法,其定義為
[X]反 =  (2.14)
(2.14)
例如, X=+0.1011, [X]反 =01011
X=-0.1011, [X]反 =10100
正數的反碼與其原碼、補碼相同。
反碼的性質:
① 在反碼表示中,機器數最高位為符號位,0代表正號,1代表負號,負數的機器數和它的真值之間的關系為:
[X]反 = ((2-2-n)+X) MOD(2-2-n)
用反碼進行兩數相加時,若最高位有進位,還必須把該進位值加到結果的最低位,才能得到真正的結果,這一操作通稱 "循環進位"。
X= +0.1011, Y=-0.0100,有[X]反 =01011, [Y]反 =11011,
[X+Y]反 = [X]反 + [Y]反 = 01011 + 11011 = 100110,最高位有進位,要加到結果的最低位,得 00110 + 00001 = 00111,即 +0.0111。
又如, X= +0.1011, Y= +0.0100,[X+Y]反 = [X]反 + [Y]反 = 01011+00100=01111,最高位無進位值,得到的已是最終結果。
② 在反碼表示中,零有兩個編碼,即
[+0.0]反 = 00000 , [-0.0]反 = 11111
有人也稱反碼為1的補碼(One's Complement),它的實際模為2-2-n。這里的-n為最低位的位序號。
用反碼實現算術運算不方便,0值又有兩個編碼,用得不很普遍。
 電子發燒友App
電子發燒友App










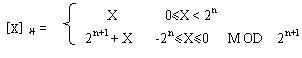










評論