原碼一位乘法的實現算法(一)

　　用原碼實現乘法運算是十分方便的。原碼表示的兩個數相乘，其乘積的符號為相乘兩數符號的異或值，數值則為兩數絕對值之積。
假定 [X]_原 = X_SX₁ X₂… X_n
　　　　 [Y]_原 = Y_SY₁Y₂… Y_n
　　　則 [X*Y]_原 = [X]_原 * [Y]_原
　　　　　　　　 = (X_S⊕Y_S) (X₁X₂ … X_n) * (Y₁ Y₂ … Y_n)
　　結果是把符號位和數值鄰接起來。

　　為了引出在計算機中實現定點原碼一位乘法的具體方案，先看手工乘法運算的實際執行步驟。
　　假定： 　　X= 0.1101 　　Y= 0.1011
　　　　　　　0. 1 1 0 1
　　　　　　* 0. 1 0 1 1
　　　　　
　　　　　　　　 1 1 0 1 　　　　　X*Y = 0.10001111，符號為正
　　　　　　　 1 1 0 1
　　　　　　 0 0 0 0
　　　　　 1 1 0 1
　　　　
　　0. 1 0 0 0 1 1 1 1

　　在手工計算時，其算法與執行步驟：
　　① 依乘數每一位上的取值為1還是為0，決定相加數取被乘數的值還是取零值；
　　② 各相加數從乘數的最低位求起，逐位變高并將相加數逐個左移一位，最后一步一次求和；
　　③ 符號位按正乘正、負乘負結果的符號位為正，正乘負、負乘正結果的符號為負的方案求出乘積的符號。

　　在計算機內實現原碼乘法運算，則不能簡單照搬上述方法，主要表現在以下諸方面。

　　首先，在運算器內是很難實現多個數據同時相加的，通常只能完成對兩數的求和操作。這一點比較容易解決，可以每求得一個相加數，就同時完成與上一次部分積相加的操作；

　　其次是在手工計算時，各相加數逐個左移一位，最終相加數的位數為相乘二數位數的兩倍，而在計算機中，加法器的位數一般與寄存器的位數相同，而不是寄存器位數的兩倍。這實際上也可以用另外的辦法加以解決。手工計算時，各相加數是逐位左移一位，但很容易發現，在計算機內，在每次計算本次部分積之和時，前一次部分積的最低一位是不再參與相加計算的。這就意味著，若采用每求得一次部分積之后使其右移一位，則可以只用N位的加法器就能實現兩個N位的數相乘，并有可能求得雙倍位數的乘積。顯而易見，若前一次部分積已經右移一位，就可以用其高位部分，再用加被乘數或加零的方法求得本次的部分積。

　　最后一點，手工計算時，乘數每一位的值是0還是1都能直接看見，而在計算機內，若采用放乘數的寄存器的每一位來直接決定本次相加數是被乘數還是零，實現起來是不方便的，若均采用該寄存器的最低一位來執行這種判別就簡便多了。為此，可以在每求一次部分積，使放乘數的寄存器執行一次右移操作即可實現。若移位時，使其最高一位數值位接收加法器最低位的移位輸出，則完成乘法運算后，該寄存器中保存的將是乘積的低位部分，而原來的乘數在逐位移位過程中已經丟失。

　　計算機內求乘積的符號，很容易用求相乘二數符號的半加和(異或值)實現。
　　有了上述說明,我們就可以得到如圖2.6所示的實現原碼一位乘法的邏輯電路框圖。


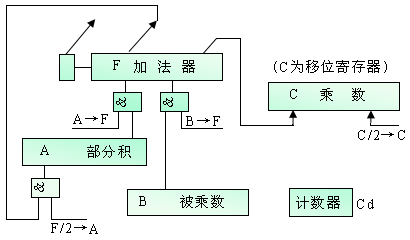
圖2.6 實現原碼一位乘法運算的邏輯線路框圖

　　乘法開始時,A寄存器被清為零,作為初始部分積。被乘數放在B寄存器中,乘數放在C寄存器中。實現部分積和被乘數相加是通過給出A→F命令和B→F命令實現的,部分積右移一位送A寄存器是通過把 F右斜一位的命令F/2→A來控制完成的，用F A命令完成把運算器的輸出直接（不移位）送到A寄存器。

　　C寄存器是用移位寄存器實現的,本身能在移位命令C/2→C控制下自行移位,其最低位的值可用作B→F的控制命令。請注意,加法器最低一位的值,右移時將移入C寄存器的最高數值位,使相乘之積的低位部分保存進C寄存器中,原來的乘數在逐位右移過程中丟失了。
圖上還給出了一個計數器T,用來控制逐位相乘的次數。它的初值經常放乘數位數的補碼值,以后每完成一位乘計算就使其計數一次,待計數到0時,給出結束乘運算的控制信號。

　　圖上未畫出求結果的符號的電路,可以通過對相乘兩數的符號執行異或操作完成。

原碼一位乘法的實現算法(二)

　　用原碼實現乘法運算是十分方便的。原碼表示的兩個數相乘，其乘積的符號為相乘兩數符號的異或值，數值則為兩數絕對值之積。

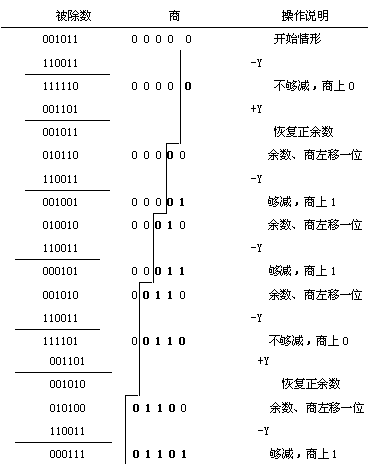
下面是恢復余數除法的一個例子。
　　假定 X=0.1011 , Y=0.1101, 則有 [X]_補 = 00 1011
　　　　　　　　 [Y]_補 = 00 1101 , [-Y]_補 = 11 0011

　　除法計算結束,二數符號異或為0,商是 +0.1101,余數為0.0111 * 2-4 ,余數0111是左移4次后得到的結果,所以真正的結果為這個值乘上2-4。若最后一次的余數為負,正確的余數應為 +Y 恢復后的正余數乘上2-4 。

　　這種方法的缺點是明顯的，當某一次 -Ｙ的差值為負時，要多一次＋Y恢復正余數的操作,降低了執行速度,又使控制線路變得復雜,因此在計算機中很少采用。在計算機中普遍采用的是不恢復余數的除法方案,它是對恢復余數除法的一種修正措施,即當某一次減得的差值為負時,不是恢復它為正差值后再繼續運算,而是設法直接用這個負的差值直接求下一位商,其實現原理敘述如下:

　　在恢復余數的除法運算中,若第i-1次求商時的余數為 +R_i-1 ,本次上商為1，下一次求商用的辦法是
　　　　R_i= 2R_i-1 - Y

　　當Ri < 0時,第i位的商上0,而恢復余數的操作結果應為Ri + Y,下一次,即第i+1次求商的減法操作是
　　　　R_i+1= 2 (R_i+ Y ) - Y = 2 R_i + 2Y - Y = 2R_i+ Y

　　上述公式表明,當某一次求商,其減得的差值為負,即R<0時,本次上商為0,繼續求下一位商時,可以不必恢復正余數,而是直接將負的差值左移一位(得2R)后,再采用加上除數的辦法來完成,即通過判別2R+Y運算的結果為正還是為負。由此可得出不恢復余數的除法運算規則為:
　
　　當余數為正時,商上1,求下一位商的辦法,是正余數左移一位,用減去除數的辦法得到;
　　余數為負時,商上0,求下一位商的辦法,是負余數左移一位,用加上除數的辦法得到。即在本方案中,在求得本位商值的同時,還要影響到用減去還是用加上除數的操作繼續求下一位商,所以不恢復余數除法又叫加減交替除法。

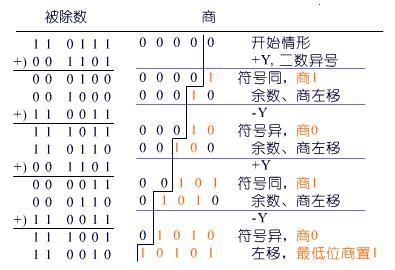
　　下面給出不恢復余數除法執行除運算過程的一個例子。用的還是X=0.1011,Y=0.1101這兩個值, [X]_補 = 00 1011 , [Y]_補 = 00 1101 , [-Y]_補 = 11 0011。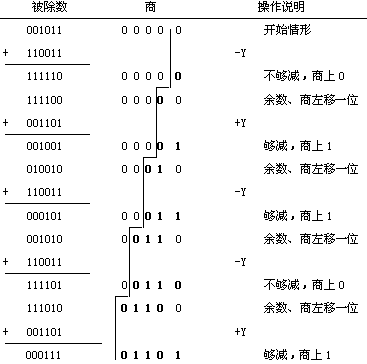


　　運算結果,商的數值位為1101,符號位為相除二數符號的異或值0,結果為+0.1101。
原碼一位除的不恢復余數的運算過程的詳細控制流程如圖2.9所示。

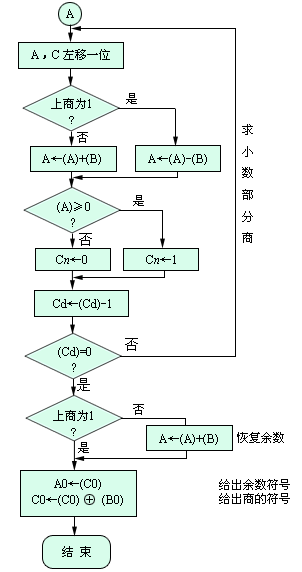
圖2.9 不恢復余數除法的運算的控制過程

　　至此,我們可把定點原碼一位除的實現方案小結如下:
　　(1) 對定點小數除法,首先要比較除數和被除數的絕對值的大小,需要防止出現數值溢出的錯誤。
　　(2) 商的符號為相除二數的符號的半加和。
　　(3) 計算機中用加減交替法實現除法運算時,被除數的位數可以是除數的兩倍,其低位的數值部分，開始時放在用于保存商的寄存器中。運算過程中,放被除數和商的寄存器同時左移一位。
　　(4) 在計算機中,求差和移位是在同一個操作步驟中完成的,而不是像我們書面寫的那種形式用兩個步驟完成。