歐姆定律
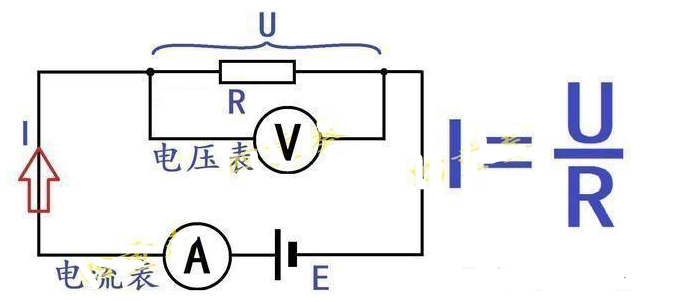
簡述:在同一電路中,導體中的電流跟導體兩端的電壓成正比,跟導體的電阻成反比,這就是歐姆定律。基本公式是I=U:R
(由歐姆定律I=U/R的推導式R=U/I不能說導體的電阻與其兩端的電壓成正比,與通過其的電流成反比,因為導體的電阻是它本身的一種性質,取決于導體的長度、橫截面積、材料和溫度,即使它兩端沒有電壓,沒有電流通過,它的阻值也是一個定值,永遠不變。)
喬治·西蒙·歐姆
歐姆(1787年—1854年)是一個刻苦很勤奮的研究者。
歐姆第一階段的實驗是探討電流產生的電磁力的衰減與導線長度的關系,其結果于1825年5月在他的第一篇科學論文中發表。在這個實驗中,他碰到了測量電流強度的困難。在德國科學家施威格發明的檢流計啟發下,他把斯特關于電流磁效應的發現和庫化扭秤方法巧妙地結合起來,設計了一個電流扭力秤,用它測量電流強度。歐姆從初步的實驗中發出,電流的電磁力與導體的長度有關。其關系式與今天的歐姆定律表示式之間看不出有什么直接聯系。歐姆在當時也沒有把電勢差(或電動勢)、電流強度和電阻三個量聯系起來。
在歐姆之前,雖然還沒有電阻的概念,但是已經有人對金屬的電導率(傳導率)進行研究。歐姆很努力,1825年7月,歐姆也用上述初步實驗中所用的裝置,研究了金屬的相對電導率。他把各種金屬制成直徑相同的導線進行測量,確定了金、銀、鋅、黃銅、鐵等金屬的相對電導率。雖然這個實驗較為粗糙,而且有不少錯誤,但歐姆想到,在整條導線中電流不變的事實表明電流強度可以作為電路的一個重要基本量,他決定在下一次實驗中把它當作一個主要觀測量來研究。
在以前的實驗中,歐姆使用的電池組是伏打電堆,這種電堆的電動勢不穩定,使他大為頭痛。后來經人建議,改用鉍銅溫差電偶作電源,從而保證了電源電動勢的穩定。
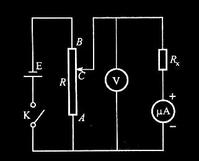
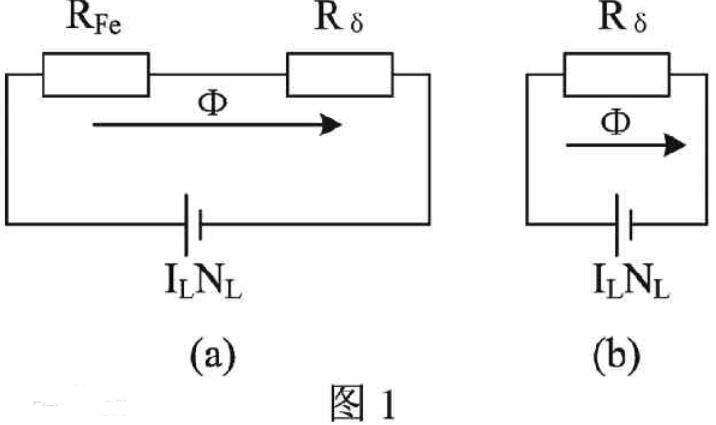
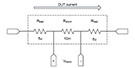
1826年,歐姆用上面圖中的實驗裝置導出了他的定律。在木質座架上裝有電流扭力秤,DD'是扭力秤的玻璃罩,CC'是刻度盤,s是觀察用的放大鏡,m和m'為水銀杯,abb'a'為鉍框架,鉍、銅框架的一條腿相互接觸,這樣就組成了溫差電偶。A、B是兩個用來產生溫差的錫容器。實驗時把待研究的導體插在m和m'兩個盛水銀的杯子中,m和m'成了溫差電池的兩個極。
歐姆準備了截面相同但長度不同的導體,依次將各個導體接入電路進行實驗,觀測扭力拖拉磁針偏轉角的大小,然后改變條件反復操作,根據實驗數據歸納成下關系:
x=q/(b+l)式中x表示流過導線的電流的大小,它與電流強度成正比,A和B為電路的兩個參數,L表示實驗導線的長度。
1826年4月歐姆發表論文,把歐姆定律改寫為:x=ksa/ls為導線的橫截面積,K表示電導率,A為導線兩端的電勢差,L為導線的長度,X表示通過L的電流強度。如果用電阻l'=l/ks代入上式,就得到X=a/I'這就是歐姆定律的定量表達式,即電路中的電流強度和電勢差成正比而與電阻成反比。為了紀念歐姆對電磁學的貢獻,物理學界將電阻的單位命名為歐姆,以符號Ω表示。
電阻的單位歐姆簡稱歐。1歐定義為:當導體兩端電勢差為1伏特,通過的電流是1安培時,它的電阻為1歐。
一個導體的電阻R不僅取決于導體的性質,它還與工作點的溫度有關。對于有些金屬、合金和化合物,當溫度降到某一臨界溫度T°C時,電阻率會突然減小到無法測量,這就是超導電現象。
導體的電阻與溫度有關。一般來說,金屬導體的電阻會隨溫度升高而增大,如電燈泡中鎢絲的電阻。半導體的電阻與溫度的關系很大,溫度稍有增加電阻值即會減小很多。通過實驗可以找出電阻與溫度變化之間的關系,利用電阻的這一特性,可以制造電阻溫度計(通常稱為“熱敏電阻溫度計”)。
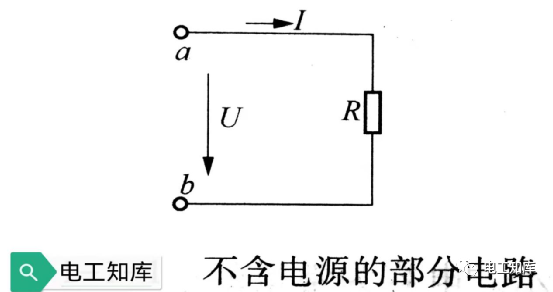
部分電路歐姆定律
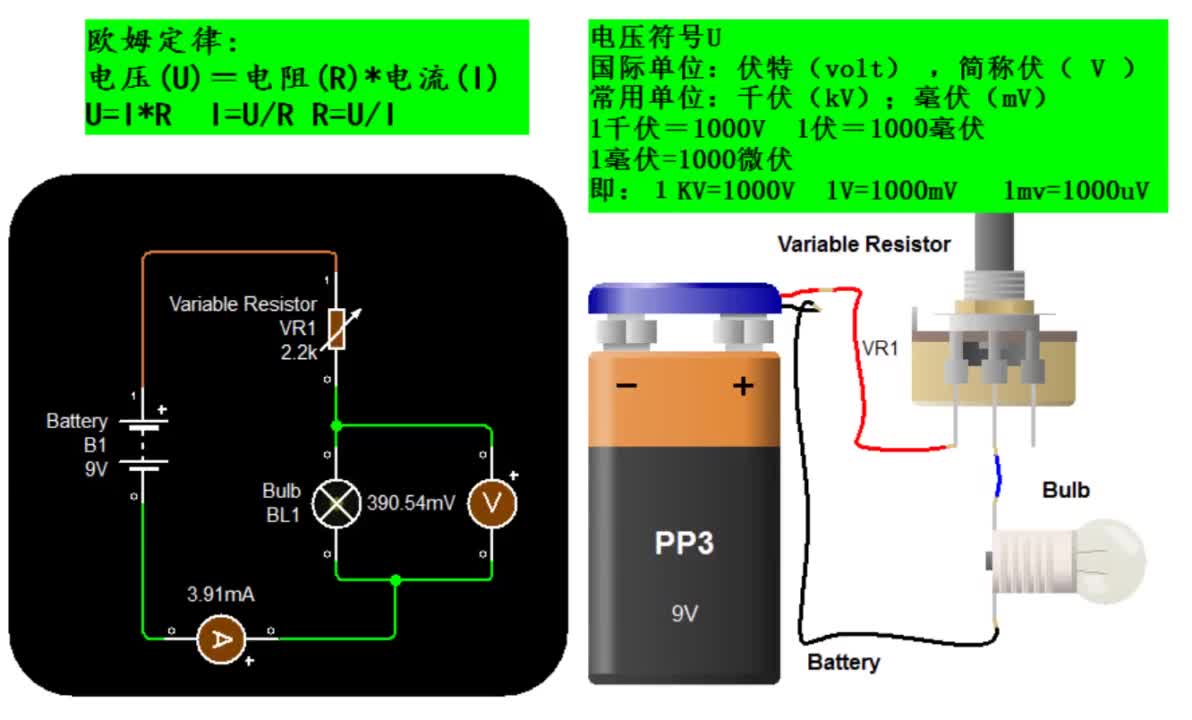
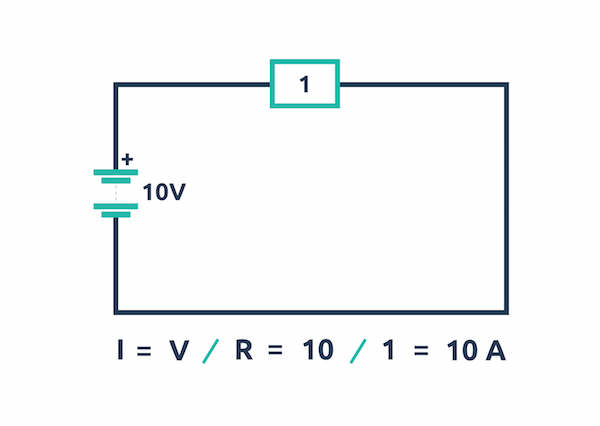
部分電路歐姆定律公式:I=U/R
其中:I、U、R——三個量是屬于同一部分電路中同一時刻的電流強度、電壓和電阻。
I=Q/t 電流=電荷量/時間 (單位均為國際單位制)
也就是說:電流=電壓/ 電阻
或者 電壓=電阻×電流『只能用于計算電壓、電阻,并不代表電阻和電壓或電流有變化關系』
歐姆定律通常只適用于線性電阻,如金屬、電解液(酸、堿、鹽的水溶液)。
由歐姆定律所推公式:
串聯電路:
I總=I1=I2(串聯電路中,各處電流相等)
U總=U1+U2(串聯電路中,總電壓等于各處電壓的總和)
R總=R1+R2+......+Rn
U1:U2=R1:R2
并聯電路:
I總=I1+I2(并聯電路中,干路電流等于各支路電流的和)
U總=U1=U2 (并聯電路中,電源電壓與各支路兩端電壓相等)
1/R總=1/R1+1/R2
I1:I2=R2:R1
R總=R1·R2\(R1+R2)
R總=R1·R2·R3:R1·R2+R2·R3+R1·R3
即1/R總=1/R1+1/R2+……+1/Rn
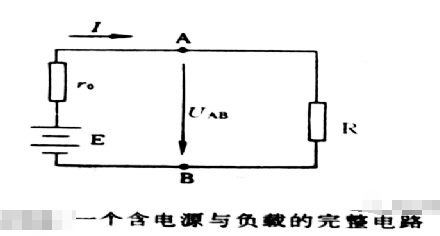
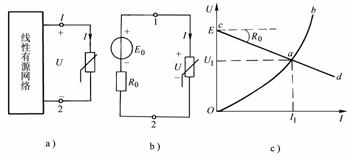
全電路歐姆定律(閉合電路歐姆定律)
I=E/(R+r)
V-電壓-伏特
R-電阻-歐姆
I-電流-安培
其中E為電動勢,r為電源內阻,內電壓U內=Ir,E=U內+U外
適用范圍:純電阻電路
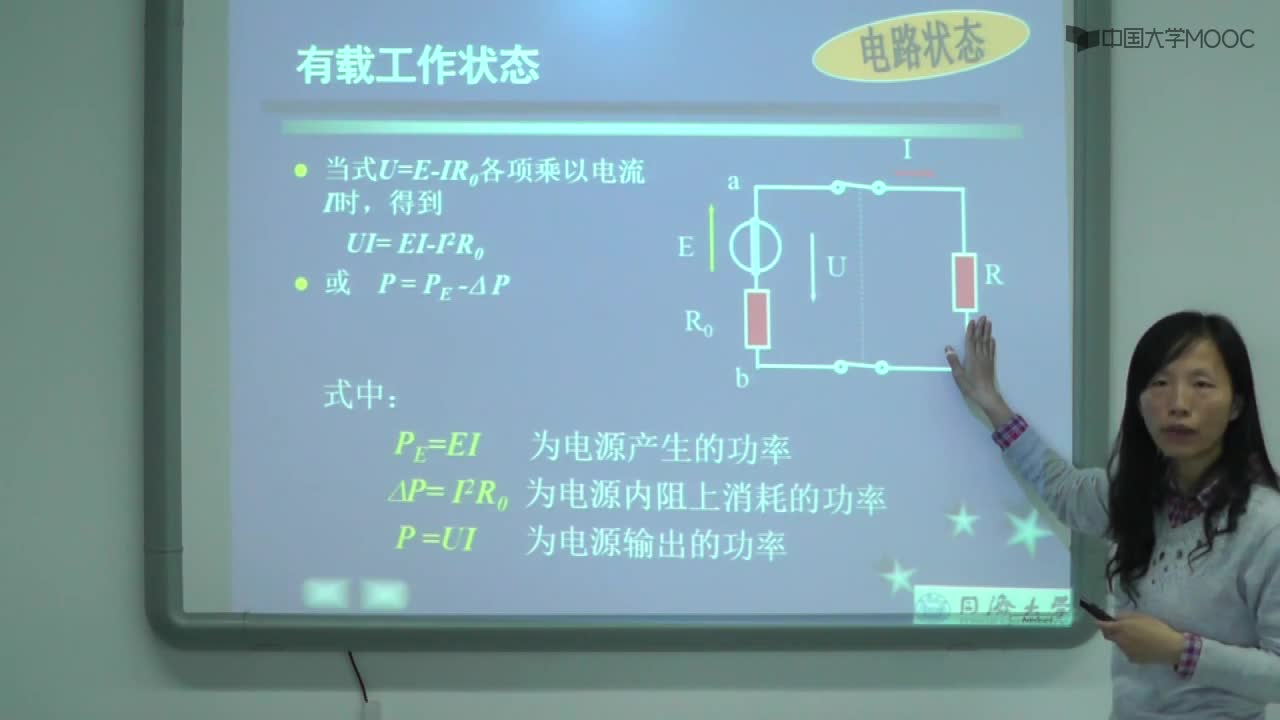
閉合電路中的能量轉化:
E=U+Ir
EI=UI+I^2R
P釋放=EI
P輸出=UI
純電阻電路中
P輸出=I^2R
=E^2R/(R+r)^2
=E^2/(R^2+2r+r^2/R)
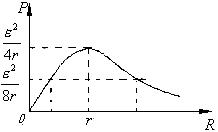
當 r=R時 P輸出最大,P輸出=E^2/4r (均值不等式)
功率與電阻的關系
歐姆定律例題
1.由歐姆定律導出的電阻計算式R=U/I,以下結論中,正確的為A、加在導體兩端的電壓越大,
則導體的電阻越大B、 通過導體的電流越大,則導體的電阻越小C、 導體的電阻跟它兩端的電壓成正比,跟電流成反比D、導體的電阻值等于導體兩端的電壓與通過導體的電流的比值。
2、一個導體兩端加有電壓為6V時,通過它的電流大小為0.2A,那么該導體的電阻為 Ω,若兩端的電壓為9V時,通過導體的電流為 A。若電路斷開,那么通過導體的電流為 A。此導體的電阻為 Ω。
3、 一個導體兩端的電壓為15V時,通過導體的電流為3A,若導體兩端的電壓增加3V,那么此時通過導體的電流和它的電阻分別為
A 0.6A 5Ω B 3.6A 5Ω
C 3.6A 1Ω D 4A 6Ω
4、一只電阻當其兩端電壓從2V增加到2.8V時,通過該電阻的電流增加了0.1A,那么該電阻的阻值為
A 8Ω B 20Ω
C 28Ω D 18Ω
5、一個定值電阻阻值為20Ω,接在電壓為2V的電源兩端。那么通過該電阻的電流是 A。若通過該電阻的電流大小為0、15A,則需要在電阻兩端加上 V的電壓。
6、有甲、乙兩個導體,甲導體的電阻是10Ω,兩端電壓為3V;乙導體電阻是5Ω,兩端電壓為6V。那么通過兩導體的電流
A I甲=6V/10Ω=0.6A I乙=3V/10Ω=0.3A
B I甲=3V/10Ω=0.6A I乙=6V/5Ω=0.3A
C I甲=6V/5Ω=1.2A I乙=6V/10Ω=0.6A
D I甲=3V/10Ω=0.3A I乙=3V/5Ω=0.6A
歐姆定律的微分形式
在通電導線中取一圓柱形小體積元,其長度ΔL,截面積為ΔS,柱體軸線沿著電流密度J的方向,則流過ΔS的電流ΔI為:
ΔI=JΔS
由歐姆定律:ΔI=JΔS=-ΔU/R 由電阻R=ρΔL/ΔS,得:
JΔS=-ΔUΔS/(ρΔL)
又由電場強度和電勢的關系,-ΔU/ΔL=E,則:
J=1/ρ*E=σE
(E為電場強度,σ為電導率)
有關歐姆定律的公式(包括推出來的)
有關歐姆定律的公式(包括推導出來的)
由歐姆定律所推公式:
并聯電路: 串聯電路
I總=I1+I2 I總=I1=I2
U總=U1=U2 U總=U1+U2
1:R總=1:R1+1:R2 R總=R1+R2R
I1:I2=R2:R1 U1:U2=R1:R2
R總=R1+R2:R1R2
R總=R1R2R3:R1R2+R2R3+R1R3
也就是說:電流=電壓÷電阻
或者 電壓=電阻×電流
流過電路里電阻的電流,與加在電阻兩端的電壓成正比,與電阻的阻值成反比。
⑴串聯電路 P(電功率)U(電壓)I(電流)W(電功)R(電阻)T(時間)
電流處處相等 I1=I2=I
總電壓等于各用電器兩端電壓之和 U=U1+U2
總電阻等于各電阻之和 R=R1+R2
U1:U2=R1:R2
總電功等于各電功之和 W=W1+W2
W1:W2=R1:R2=U1:U2
P1:P2=R1:R2=U1:U2
總功率等于各功率之和 P=P1+P2
⑵并聯電路
總電流等于各處電流之和 I=I1+I2
各處電壓相等 U1=U1=U
總電阻等于各電阻之積除以各電阻之和 R=R1R2÷(R1+R2)
總電功等于各電功之和 W=W1+W2
I1:I2=R2:R1
W1:W2=I1:I2=R2:R1
P1:P2=R2:R1=I1:I2
總功率等于各功率之和 P=P1+P2
⑶同一用電器的電功率
①額定功率比實際功率等于額定電壓比實際電壓的平方 Pe/Ps=(Ue/Us)的平方
2.有關電路的公式
⑴電阻 R
①電阻等于材料密度乘以(長度除以橫截面積) R=密度×(L÷S)
②電阻等于電壓除以電流 R=U÷I
③電阻等于電壓平方除以電功率 R=UU÷P
⑵電功 W
電功等于電流乘電壓乘時間 W=UIT(普式公式)
電功等于電功率乘以時間 W=PT
電功等于電荷乘電壓 W=QU
電功等于電流平方乘電阻乘時間 W=I×IRT(純電阻電路)
電功等于電壓平方除以電阻再乘以時間 W=U?U÷R×T(同上)
⑶電功率 P
①電功率等于電壓乘以電流 P=UI
②電功率等于電流平方乘以電阻 P=IIR(純電阻電路)
③電功率等于電壓平方除以電阻 P=UU÷R(同上)
④電功率等于電功除以時間 P=W:T
⑷電熱 Q
電熱等于電流平方成電阻乘時間 Q=IIRt(普式公式)
電熱等于電流乘以電壓乘時間 Q=UIT=W(純電阻電路)
 電子發燒友App
電子發燒友App














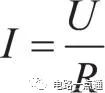

























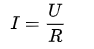

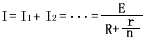











評論