摘要

　　是否曾想過為什么一個設計能夠以高于設計團隊承諾的頻率工作?為何該設計團隊不能將這個更高的頻率當作要實現的目標?

　　過去，靜態時序分析被用來分析SoC是否能夠在規定的目標頻率工作。時序驗收要么在最差情況(WCS)，要么在最佳情況(BCS)下完成。通常，這些與三西格瑪區域對應。當然，為了結束這些情況下的時序，可能進行了大量過度設計。

　　統計靜態時序分析(SSTA)嘗試采用一種方法來減少這種不必要的過度設計，因此努力讓設計變得更加切合實際，并同時幫助提高目標頻率。

　　什么是統計靜態時序分析?

　　過去幾十年里，靜態時序分析(STA)一直是用來結束數字電路時序的一種常用方法。

　　但由于幾何尺寸縮小到45nm甚至更小，現在要結束時序變得越來越困難了。STA和工藝數量的增加，使得整個情形變得更為復雜。

　　之所以出現這樣的復雜情況，是因為要在高級技術節點上實現工藝變化變得異常困難了。現在共有兩種變化：

　　1.芯片到芯片變化

　　2.芯片內變化

　　這兩種變化又可以進一步劃分為：

　　1.系統性變化

　　2.隨機性變化

　　其中的部分變化目前仍算在傳統的STA方法內。SSTA嘗試按概率分布來考慮所有這些變化。

　　基本上，SSTA會計算概率函數，以計算每個節點上每個信號的到達時間。如果設計達到規定的目標頻率，根據到達時間的概率分布函數，就能將它計算出來。

　　例如，如果概率為97%，那么最小余量的信號的到達時間為5ns;到達時間為4ns的概率為10%。這意味著200MHz的目標頻率其得到的概率應為97%，250MHz的目標頻率其概率為10%。

　　變化：

　　臨界尺寸的擴展速度超過了我們的控制。現在隨著技術節點的減少，互連變化與有源門相比，它正逐漸占據主導地位。

　　由于互連開始占主導地位，時序的臨界變量不只限于晶體管的臨界尺寸，同時包括線段尺寸和實際形狀以及附近網絡的數量。

　　金屬寬度、金屬厚度、經電阻、絕緣高度都具有不同的金屬層屬性。晶體管的類似屬性包括晶體管長度、寬度、摻雜密度和門氧化層厚度。

　　1.互連變化

　　這種統計法對互連領域里所有可能的變化組合建模型。例如，啟動路徑可能位于金屬3中，而獲取路徑就能夠則位于金屬4中。

　　過去，STA在所有金屬中會各不相同，因此不能將金屬3導致最大時延、金屬4導致最低時延的這種情況設立模型。此類組合對應于建立路徑的最差情況，只能從統計角度對互連變化建模來獲取。

　　2.芯片內變化：

　　目前，這是通過使用啟發式降額數，以及對最差情況和最佳情況時序模型進行片上變化分析來完成的。

　　3.芯片間變化：

　　工藝參數存在變化，這可能以類似方式對所有芯片產生影響。在STA中，這是通過WCS時序模型(慢晶體管)和BCS時序模型(快晶體管)來處理的。

　　概率密度函數(PDF)

　　在SSTA中，所有參數(隨機和系統參數)都是按概率分布函數(PDF)的角度來處理。

　　即使用的不是單個值，而是概率密度函數。下面的圖1給出了PDF示例。

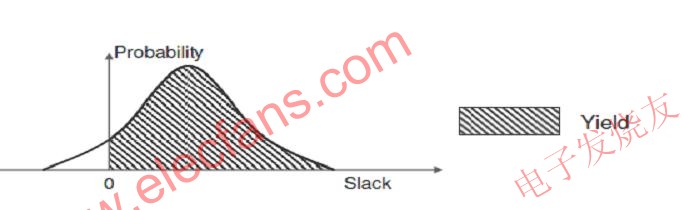
　　圖1：余量的概率密度函數(PDF)

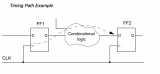
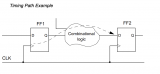
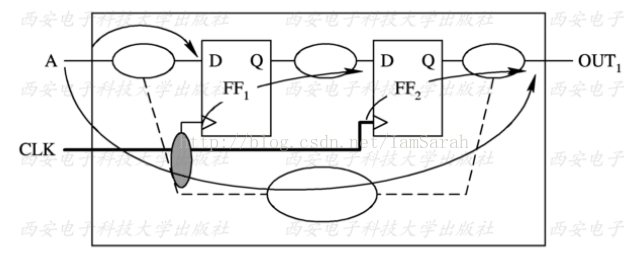
　　時序路徑舉例：

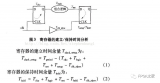
　　下面給出了時序路徑的一個例子(圖2)。時序路徑的PDF如下圖所示(圖3)。這個PDF是通過對門時延PDF和到達時間統計分析后計算得到的。

　　到達時間、余量、壓擺等都采用Taylor系列儀器計算得出。

　　a0+∑i=1,n(ai?Gi)+an+1?Ra

　　其中，

　　–a0是平均值

　　–?Gi是“n”全局源變化

　　–ai描述對應Gi的統計變化

　　–?Ra是獨立隨機變量R的變化

　　–an+1描述對應Ra的統計變化。

　　平均值(μ)=a0+∑i=1,nai平均值(?Gi)+an+1平均值(?Ra)------(i)

　　標準差(σ)=[{aiStd(?Gi)}2+{an+1Std(?Ra)}2]?-(ii)

　　使用上面兩個等式，這些分布函數可以用如下方式表示：

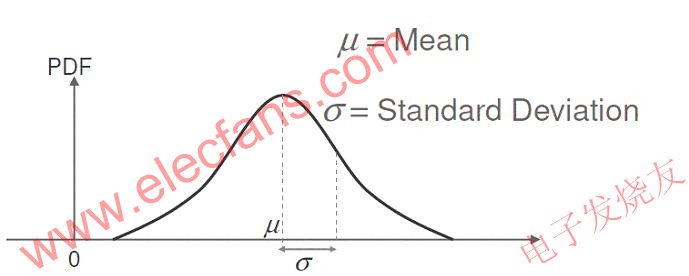
　　圖2：PDF示例

　　門時延的PDF(紅色)和到達時間(綠色)也在圖3中標記出來了。

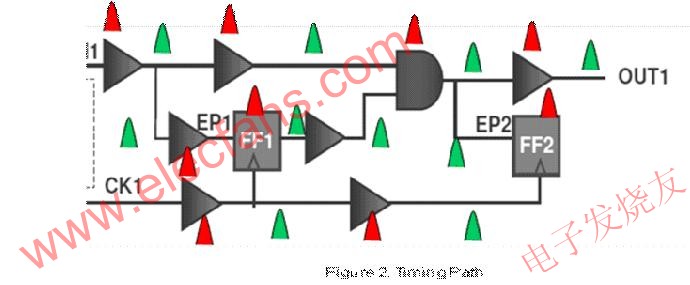
　　圖3：時序路徑

　　OUT1的PDF：

　　所示區域代表違反時序的概率。基本上，該區域代表當前目標頻率產生的損失。該PDF還對第1段提到的問題做了回答。現在，設計人員可以聲稱頻率數字考慮了結果平衡。這種情況有助于提高設計公司的利潤，因為它們可以聲稱能夠實現更接近的目標頻率。

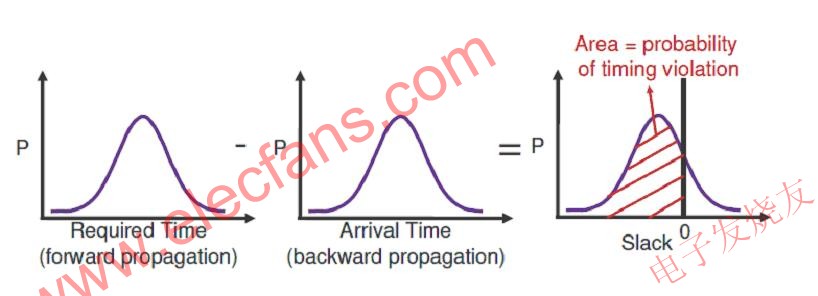
　　圖4：時序路徑的PDF

　　如上圖所示，規定時序時間和達到時間的PDF結合起來，計算分布情況。要注意的另一個方面是，在達到上圖(圖4)所示的數字之前，時鐘延遲也可以用統計方式表示。

　　SSTA–難點

　　1.概率函數很難計算。更重要的是，從統計角度看芯片上的變化不是彼此獨立的。

　　2.計算需要S–lib格式的時序模型。

　　3.由于統計數據容量大，與傳統的STA相比，該計算屬于內存密集型。

　　4.運行時間也是一個難點。

　　但是，只要記住SSTA能為設計團隊提供的優勢，所有這些難點都可以迎刃而解。

　　總結

　　與傳統的STA相比，SSTA仍處于初期階段，但它能以更切實可行的方式為設計提供收尾工作。它根據工藝和互連參數變化，對設計進行分析。