? ? ? 比例運算電路的工作原理

　　比例運算電路的輸出電壓與輸入電壓之間存在比例關系，即電路可實現比例運算。比例電路是最基本的運算電路，是其他各種運算電路的基礎，本章隨后將要介紹的求和電路、積分和微分電路、對數和指數電路等等，都是在比例電路的基礎上，加以擴展或演變以后得到的。

? ? ? 比例運算電路的分類

　　根據輸入信號接法的不同，比例電路有三種基本形式：反相輸入、同相輸入以及差分輸入比例電路。

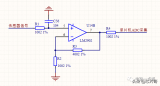
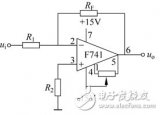
　　1、反相比例運算電路

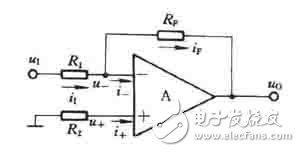
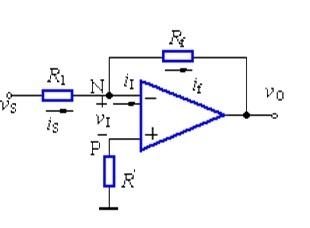
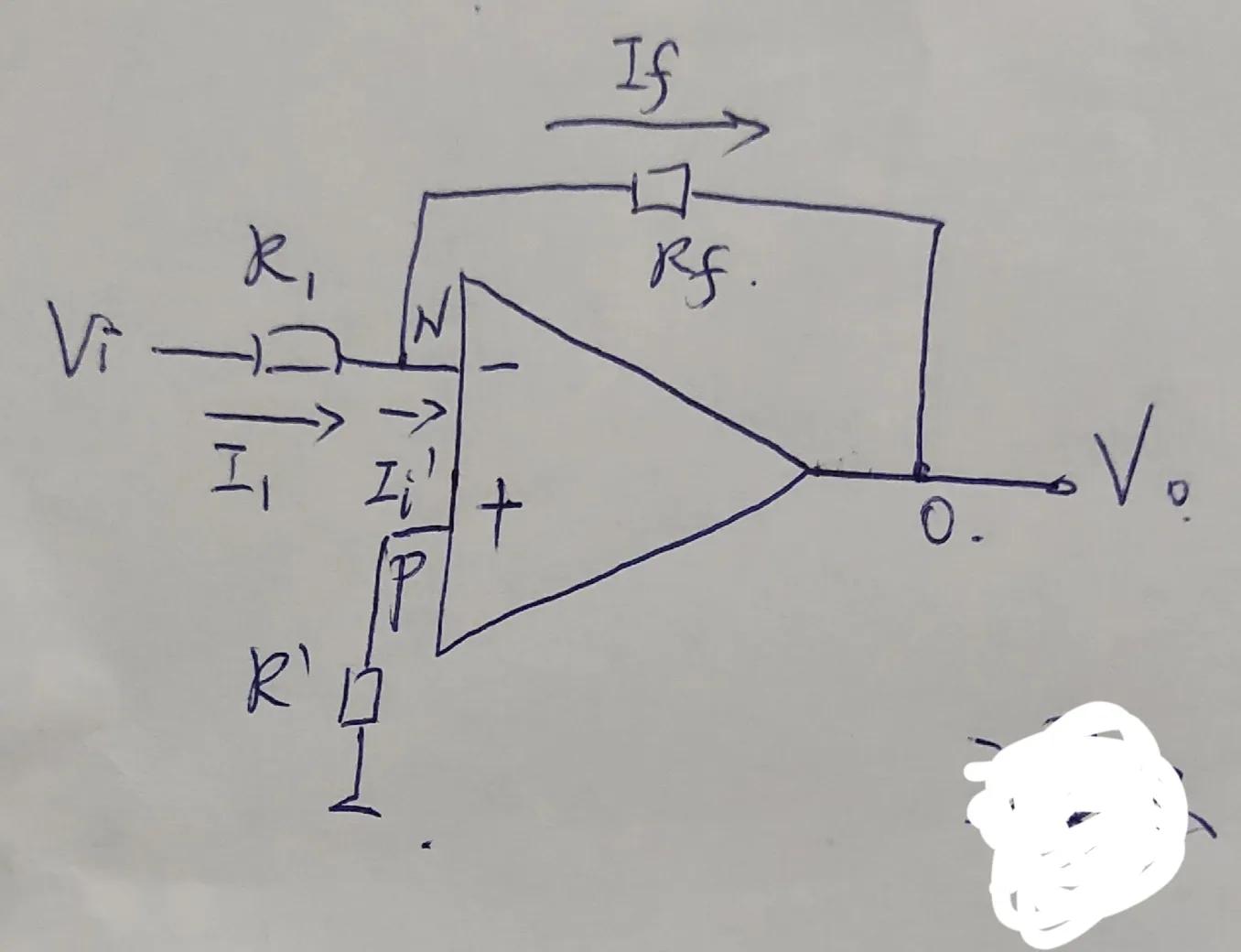
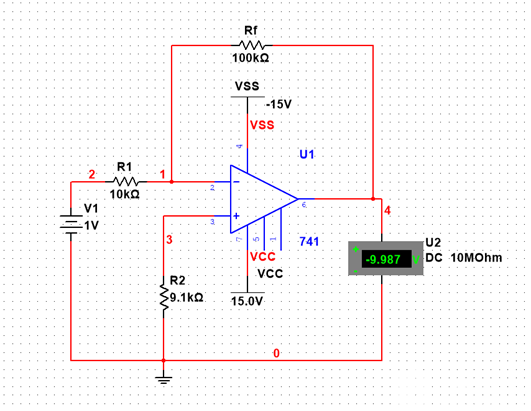
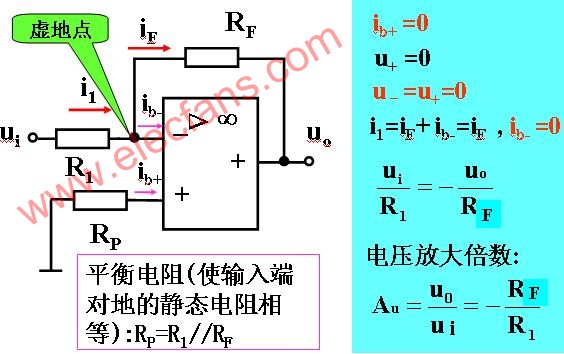
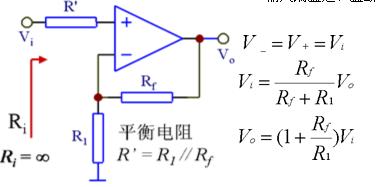
　　在上圖中，輸入電壓u1經電阻R1加到集成支放的反相輸入端，其同相輸入端經電阻R2接地。輸出電壓u0經RF接回到反相輸入端。集成運放的反相輸入端和同相輸入端，實際上是運放內部輸入級兩個差分對管的基極。為使差動放大電路的參數保持對稱，應使兩個差分對管基極對地的電阻盡量一致，以免靜態基流流過這兩個電阻時，在運放輸入端產生附加的偏差電壓。因此，通常選擇R2的阻值為

　　R2=R1 // RF （1）

　　經過分析可知，反相比例運算電路中反饋的組態是電壓并聯負反饋。由于集成運放的開環差模增益很高，因此容易滿足深負反饋的條件，故可以認為集成運放工作在線性區。因此，可以利用理想運放工作在線性區時“虛短”和“虛斷”的特點來分析反相比例運算電路的電壓放大倍數。

　　在上圖中，由于“虛斷”，故i+=0，即R2上沒有壓降，則u+=0。又因“虛短”，可得

　　u-= u+=0 （2）

　　上述說明在反相比例運算電路中，集成運放的反相輸入端與同相輸入端兩點的電位不僅相等，而且均等于零，如同該兩點接地一樣，這種現象稱為“虛地”。“虛地”是反相比例運算電路的一個重要特點。

　　由于I-=0，由由圖可見

　　iI= iF

　　即

　　上式中u-=0，由此可求得反相比例運算電路的電壓放大倍數為

　　 （3）

　　下面分析反相比例運算電路的輸入電阻。因為反相輸入端“虛地”，顯而易見，電路的輸入電阻為

　　Rif = R1 （4）

　　綜合以上分析，對反相比例運算電路可以歸納得出以下幾點結論：

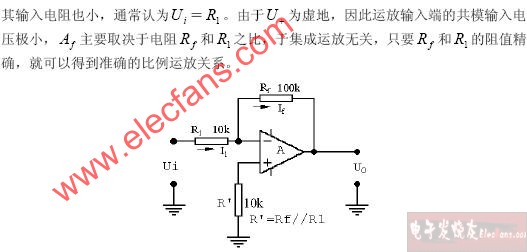
　　1）反相比例運算電路實際上是一個深度的電壓并聯負反饋電路。在理想情況下，反相輸入端的電位等于零，稱為“虛地”。因此加在集成運簇輸入端的共模輸入電壓很小。

　　2）電壓放大倍數， 即輸出電壓與輸入電壓的幅值成正比，但相位

　　相反。也就是說，電路實現了反相比例運算。比值 Auf 決定于電阻RF和R1之比，而與集成運放內部各項參數無關。只要RF和R1的阻值比較準確而穩定，就可以得到準確的比例運算關系。比值Auf 可以大于1，也可以小于1。當RF=R1時，Auf=-1，稱為單位增益倒相器。

　　3）由于引入了深度電壓并聯負反饋，因此電路的輸入電阻不高，輸出電阻很低。

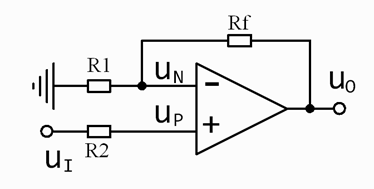
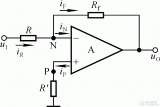
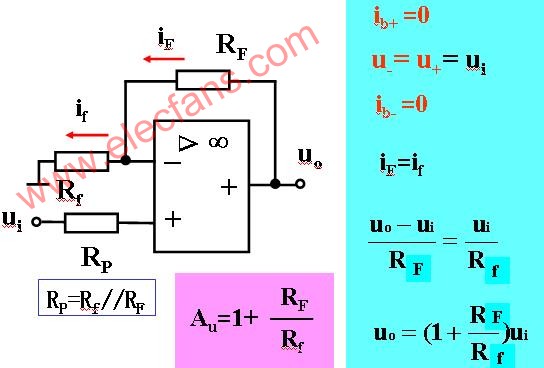
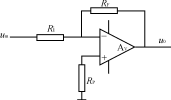
　　2、同相比例運算電路

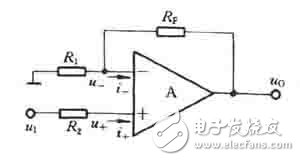
　　在上圖中，輸入電壓u1接至同相輸入端，但是為保證引入的是負反饋，輸出電壓uo通過電陰RF仍接到反相輸入端，同時，反相輸入端通過電陰R1接地。為了使集成運放反相輸入端和同相輸入端對地的電阻一致，R2的阻值仍應為

　　R2 = R1 // RF

　　同相比例運算電路中反饋的組態為電壓串聯負反饋，同樣可以利用理想運放工作在線性區時的兩個特點來分析其電壓放大位數。

　　在上圖中，根據“虛短”和“虛斷”的特點可知， i_=i+=0， 故

　　則同相比例運算電路的電壓放大倍數為

　　（5）

　　由于引入了電壓串聯負反饋，因此能夠提高輸入電阻，而且提高的程度與反饋深度有關。在理想運放條件下，即認為Aod 趨于無窮大，Rid趨于無窮大 ，則同相比例運算電路的輸入電阻Rid 趨于無窮大。當考慮Aod≠ ∞，Rid ≠ ∞的一般情況時，經過分析可知，同相比例運算電路的輸入電阻為

　　Rid = （1 + AodF）Rid （6）

　　式中Aod和Rid分別是集成運放的開環差模電壓增益和差模輸入電阻，F是反饋系數，在本電路中

　　由式（5）可知，同相比例運算電路的電壓放大倍數總是大于或等于1。

　　由于這種電路的輸出電壓與輸入電壓不僅幅值相等，而且相位也相同，二者之間是一種“跟隨”關系，所以又稱為電壓跟隨器。

　　綜上所述，對同相比例運算電路可以得到以下幾點結論：

　　1）相比例運算放大電路是一個深度的電壓串聯負反饋電路。因為u_ = u+= uI，所以不存在“虛地”現象，在選用集成運放時要考慮到其輸入端可能具有較高的共模輸入電壓。

　　2）電壓放大倍數 ，即輸出電壓與輸入電壓的幅值成正比，且相位相同。也就是說，電路實現了同相比例運算。Auf也只取決于電阻RF和R1之比，而與集成運放的內部參數無關，所以比例運算的精度和穩定性主要取決于電阻RF和R1的精確度和穩定度。一般情況下，Auf值恒大于1。當RF=0或R1=∞時，Auf=1，這種電路稱為電壓跟隨器。

　　3）由于引入深度電壓串聯負反饋，因此電路的輸入電阻很高，輸出電阻很低。

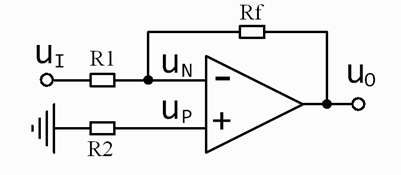
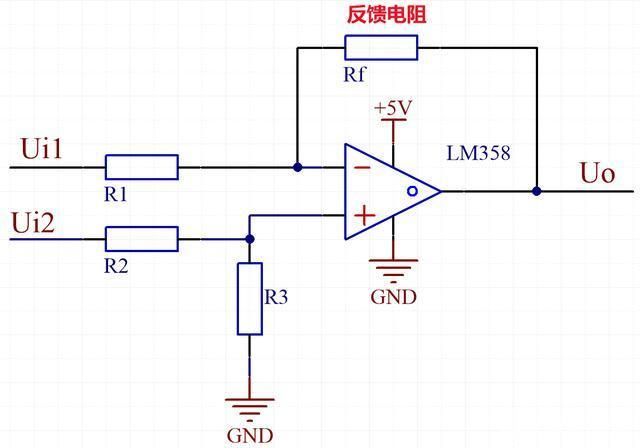
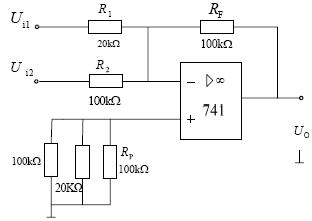
　　3、差分比例運算電路

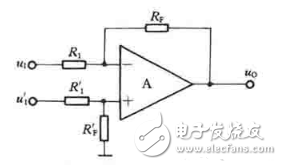
　　在上圖中，輸入電壓uI和uI’分別加在集成運放的反相輸入端和同相輸入端，從輸出端通過反饋電陰RF接回到反相輸入端。為了保證運放兩個輸入端對地的電阻平衡，同時為了避免降低共模抑制比，通常要求

　　R1= R1’

　　RF= RF’

　　在理想條件下，由于“虛斷”，i+=i_=0，利用疊加定理可求得反相輸入端的電位為

　　而同相輸入端的電位為

　　當滿足條件R1 = R1’，RF = RF’ 時，整理上式，可求得差分比例運算電路的電壓放大倍數為

　　 （8）

　　在電路元件參數對稱的條件下，差分比例運算電路的差模輸入電阻為

　　Rif = 2R1 （9）

　　由式（8）可知，電路的輸出電壓與兩個輸入電壓之差成正比，實現了差分比例運算。其比值舊|Auf|同樣決定于電阻RF和R1之比，而與集成運放內部參數無關。由以上分析還可以知道，差分比例運算電路中集成運放的反相輸入端和同相輸入端可能加有較高的共模輸入電壓，電路中不存在“虛地”現象。

　　差分比例運算電路除了可以進行減法運算以外，還經常被用作測量放大器。差分比例運算電路的缺點是對元件的對稱性要求比較高，如果元件失配，不僅在計算中帶來附加誤差，而且將產生共模電壓輸出。電路的另一個缺點是輸入電阻不夠高。

　　以上介紹了反相輸入、同相輸入和差分輸入三種基本形式的比例電路，現將它們的電路組成、電壓放大倍數、輸入和輸出電阻，以及性能特點歸納在表中，以便進行比較。

　　上述各種比例運算電路的輸入、輸出關系表達式都是在理想運放條件下得到的，但實際集成運放的各項指標不可能完全理想，因此在上述運算公式中將產生誤差。