等效變換

? ? ? ? ?等效是電路分析中一種很重要的思維方法。根據電路等效的概念，可將一個結構較復雜的電路變換成結構簡單的電路，使電路的分析簡化。

　　 等效的概念

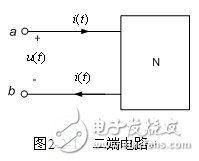
　　【二端電路（一端口電路）】 兩端電路具有以下特點：只有兩個端鈕（a，b）與外部電路相連；進出端鈕的電流相同，如圖2-2-1所示。二端電路元件，例如電阻元件、獨立源、電容元件、電感元件，可視為二端電路的特例，也稱二端元件。二端電路也稱為一端口電路，一端口電路端口電壓、電流的關系稱為一端口網絡的端口特性或端口VCR。

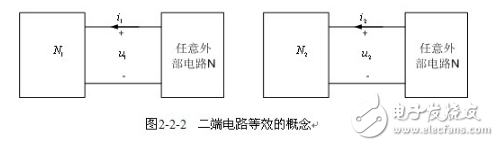
　　【等效電路】 兩個二端電路，，如圖2-2-2所示，無論兩者內部的結構如何不同，只要它們的端口電壓、電流的關系（ VCR）相同，則稱和是等效的。兩個內部結構不同的電路等效的唯一標準是兩者對應端口處的VCR完全一致，即它們對同一任意外部電路的效果完全相同。等效是對外部電路而言的，對于互相等效的兩個電路，，內部的工作狀態是不等效的。等效具有傳遞性，如果二端電路和等效，二端電路又與等效，則必有與等效。

　　電阻的串聯與并聯等效變換

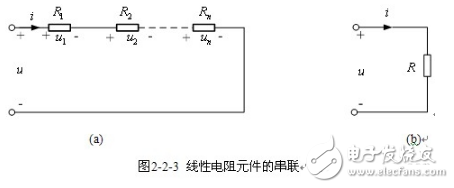
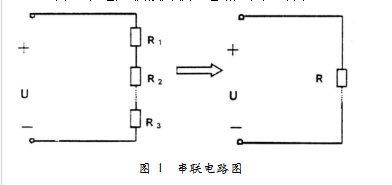
　　【電阻元件的串聯】圖2-2-3（a）中，由KVL得

　　且 　

　　由KVL得

　　令

　　則

　　根據上式可以構造一個相應電路如圖2-2-3（b）所示，所以圖（a）和（b）是等效的，等效電阻等于各串聯電阻元件電阻之和。

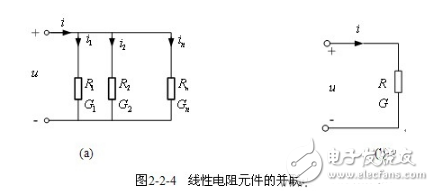
　　【電阻元件的并聯】圖2-2-4（a）中，由KCL得

　　令

　　用等效電導表示為

　　星形電阻網絡與三角形電阻網絡的等效變換

　　由線性電阻元件混聯構成的網絡，其最簡等效電路為線性電阻。但是并非所有由線性電阻元件混聯構成的網絡都能通過串、并聯化簡為線性電阻。本小節介紹“平衡電橋”和“星形-三角形”互換兩種化簡方法。通過這兩種方法，在結合電阻元件的串聯、并聯化簡，可實現任何由線性電阻混聯構成的網絡的等效化簡。

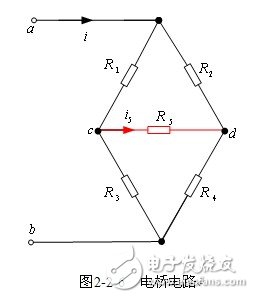
　　【平衡電橋】圖2-2-6所示由5個線性電阻（為必要條件）構成的橋式電路中，當或（由于為線性電阻，該兩個條件必是同時成立的）時，稱此橋式電路為平衡電橋。由平衡電橋電路特點可得到平衡電橋的兩種等效電路。由得到圖2-2-6所示等效電路；由得到圖2-2-6所示等效電路。

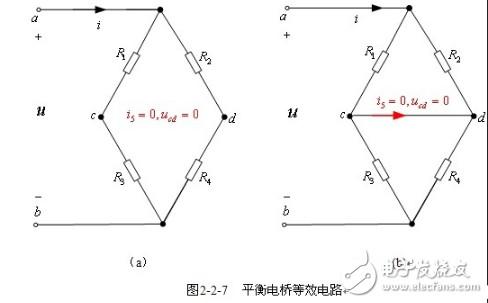
　　【電橋平衡條件】在圖2-2-7（a）所示電路中，有

　　在電路2-2-7（b）中 ，有

　　由以上兩式均可以推出電橋平衡的條件，為

　　【星形—三角形互換】 當電橋不滿足平衡條件時，必須采用星形（Y形）與三角形（△形）互換才能將電橋電路化成線性電阻。

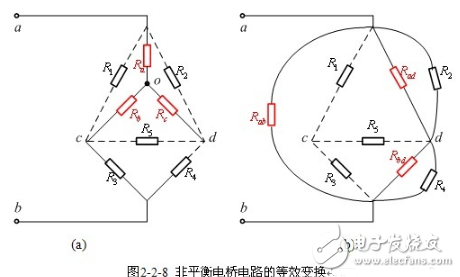
　　如果可將圖2-2-6中以節電a，c，d為頂點的三角形電阻，和等效變換成圖2-2-8（a）中以新節點o為中心的星形連接電阻，和；或者將圖2-2-6中，以c為中心的Y形連接電阻，和等效變換成圖2-2-8（b）中以節點a，b，d為頂點的△形連接電阻，和。這樣各電阻之間連接關系成為串聯和并聯關系了。也可以選擇△cbd變成Y形，或選擇以d為頂點的Y形變為△形。

　　【星形—三角形互換條件】根據前面等效的概念，分別求出這兩種電路端鈕處的電壓-電流關系，讓兩者相同，即可獲得等效條件。

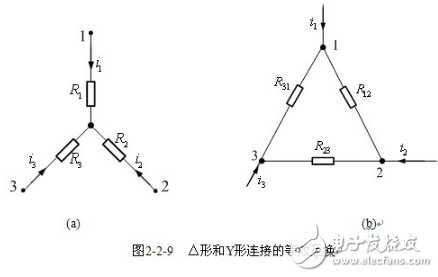
　　在△形電路中，有

　　求解得△形電路中的電壓-電流關系

　　而Y形電路中的電壓-電流關系為

　　兩種電路等效，則端鈕處的電壓-電流關系應相同。比較△形電路和Y形電路的電壓-電流關系，可得△形電路等效變換成Y形電路的條件為

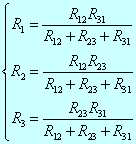　　 （△→Y）

　　同理可得Y形電路等效變換成△形電路的條件為

　　 （Y→△）

　　【例2-2-1】 求圖2-2-10（a）所示電路的電流I。

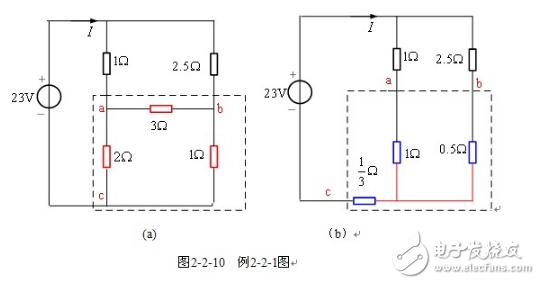
　　將圖2-2-10（a）中，，所構成的三角形電路按等效變換為（b）所示電路。則

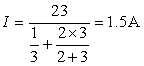
　　4、實際電源的兩種模型及其等效變換

　　獨立電源是可以用來描述實際電源的電路元件。以下討論實際直流電源的電路模型。

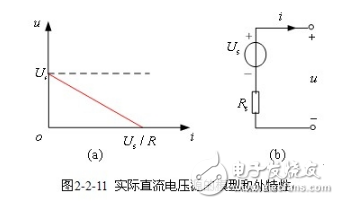
　　【實際直流電壓源模型（戴維寧模型）】 一個實際直流電壓源的端電壓并不是恒定不變的，而是隨著輸出電流的增加而下降。實際直流電壓源外部特性可用圖2-2-11（a）所示曲線描述。根據曲線的形狀可用獨立電壓源和線性電阻元件串聯的模型來等效，圖2-2-11（b）為該實際電源的電路模型，稱為戴維寧模型。模型特性方程為

　　當實際電壓源內阻很小時，特性曲線趨于與i軸平行，當時，特性曲線與i軸平行，成為理想電壓源。

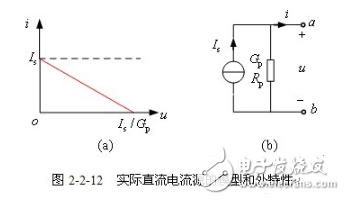
　　【實際直流電流源模型（諾頓模型）】 一個實際直流電流源，其電流并不是恒定不變的，而是隨著端電壓的增大而下降。實際直流電流源外部特性可用圖2-2-12（a）所示曲線描述，并用圖2-2-12（b）所示電路模型來等效，稱為諾頓模型，電路模型的端口的特性方程為

　　當實際電流源內電導很小時，特性曲線趨于與u軸平行，當時，實際電流源成為獨立電流源。

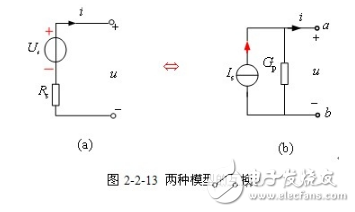
　　【戴維寧模型和諾頓模型的互換】 圖2-2-13（a）實際電壓源端口電壓-電流關系為

　　圖2-2-13（b）實際電流源端口電壓-電流關系為

　　欲使兩種模型等效，則要求端口電壓-電流關系相同，由此可得出元件參數應滿足

　　或者

　　進行等效變換時應注意：

　　（1）電流源電流的參考方向由電壓源的負極指向正極；

　　（2）等效是對外部電路而言的，對兩電路內部的電阻之間、電壓源和電流源之間是不等效的；

　　（3）等效變換條件也適用于受控電壓源構成的戴維寧支路和受控電流源構成的諾頓支路，注意在電路變換中控制支路應保留。

　　5、電源等效轉移

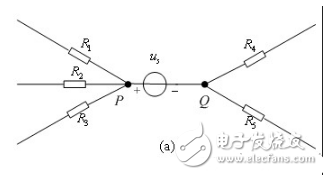
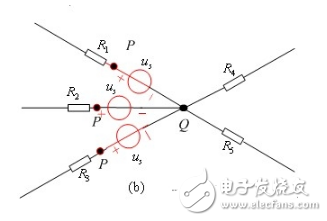
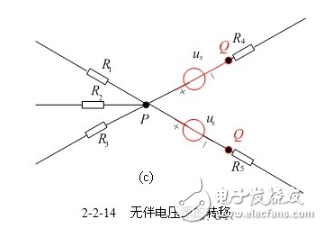
　　【無伴電壓源轉移】電壓源沒有與之串聯的電阻而單獨成為一條支路，稱為無伴電壓源支路，圖2-2-14（a）所示無伴電壓源可以進行以下等效變換。圖2-2-14（b）是按P節點轉移，圖2-2-14（c）是按Q點轉移。本質上是將電壓源按照結點所連支路數裂開，注意圖中結點的變化。

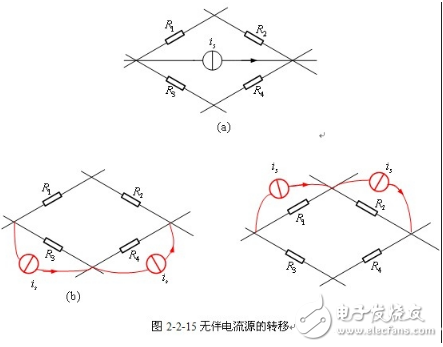
　　【無伴電流源轉移】電流源沒有與之并聯的電阻而單獨成為一條支路，稱為無伴電流源支路。無伴電流源可進行以下等效變換。變換規則為：將電流源順其原來的參考方向，轉移到包含電流源的任意一個回路中的各支路上，并與這些支路并聯，原無伴電流源所連接的兩節點之間開路。