確定k個劃分達到平方誤差最小。適用于發現凸面形狀的簇,簇與簇之間區別較明顯,且簇大小相近。
優點
算法快速,簡單;對大數據集有較高的效率并且可伸縮;時間復雜度為O(n*k*t), 其中t是迭代次數,接近于線性,并且適合挖掘大規模數據集。
缺點
k值的選定難以估計,初始類聚類中心點的選取對聚類結果有較大的影響。經常以局部最優結束,對噪聲和孤立點敏感。
算法過程
輸入:k,data
1) 選取k個點作為質心;
2) 計算剩余的點到質心的距離并將點歸到最近的質心所在的類;
3) 重新計算各類的質心;
4) 重復進行2~3步直至新質心與原質心的距離小于指定閾值或達到迭代上限
優化目標
聚類的基本假設:對于每一個簇,可以選出一個中心點,使得該簇中的所有的點到該中心點的距離小于到其他簇的中心的距離。雖然實際情況中得到的數據并不能保證總是滿足這樣的約束,但這通常已經是我們所能達到的最好的結果,而那些誤差通常是固有存在的或者問題本身的不可分性造成的。
基于以上假設,N個數據點需要分為K個簇時,k-means要優化的目標函數:
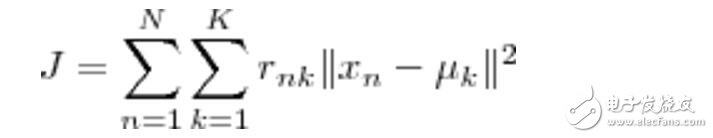
其中,在數據點n被歸類到簇k的時候為1,否則為0。
為第k個簇的中心。
直接尋找和來最小化J并不容易,不過可以采取迭代的辦法:先固定 ,選擇最優的 ,很容易看出,只要將數據點歸類到離他最近的那個中心就能保證 J最小。下一步則固定,再求最優的。將 J對求導并令導數等于零,很容易得到J 最小的時候 應該滿足:
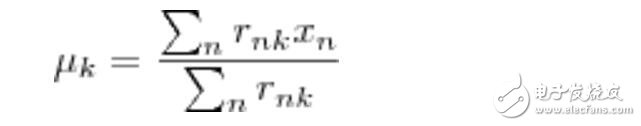
即 的值應當是所有簇k中的數據點的平均值。由于每一次迭代都是取到 J的最小值,因此J 只會不斷地減小(或者不變),而不會增加,這保證了k-means最終會到達一個極小值。雖然k-means并不能保證總是能得到全局最優解,但是對于這樣的問題,像k-means這種復雜度的算法,這樣的結果已經是很不錯的了。
kmeans方法應用舉例
[plain] view plain copy#顯示數據的基本特征
#檢查數據的維度
dim(iris)
#顯示列名
names(iris)
#查看數據內部結構
str(iris)
#顯示數據集屬性
attributes(iris)
#查看前十行記錄
head(iris,10)
iris[1:10,]
#查看屬性Petal.Width的前五行數據
iris[1:5,“Petal.Width”]
iris$Petal.Width[1:5]
#顯示每個變量的分布情況
summary(iris)
#顯示iris數據集列Species中各個值出現的頻次
table(iris$Species)
#根據列Species畫出餅圖
pie(table(iris$Species))
#畫出Sepal.Length的分布柱狀圖
hist(iris$Sepal.Length)
#畫出Sepal.Length的密度函數圖
plot(density(iris$Sepal.Length))
#畫出Sepal.Length列和Petal.Length列的散點圖
plot(iris$Sepal.Length,iris$Petal.Length)
#計算Sepal.Length列所有值的方差
var(iris$Sepal.Length)
#計算Sepal.Length列和Petal.Length列的協方差
cov(iris$Sepal.Length, iris$Petal.Length)
#計算Sepal.Length列和Petal.Length列的相關系數
cor(iris$Sepal.Length, iris$Petal.Length)
#使用Kmeans聚類
#刪去類別列,即第五列,然后對數據做聚類
#1
newiris = iris[,-5]
#2
newiris = iris
newiris$Species = NULL
#將數據分為三類
class = kmeans(newiris, 3)
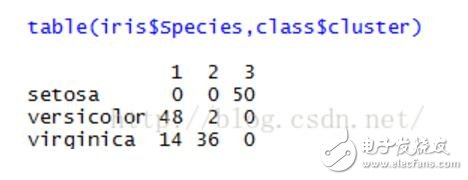
#統計每種花中屬于每一類的數量
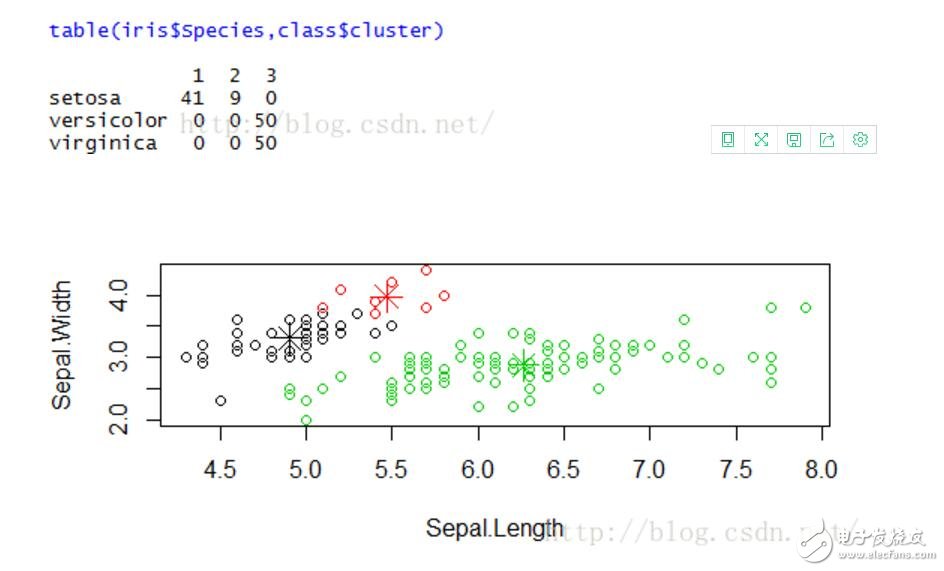
table(iris$Species,class$cluster)
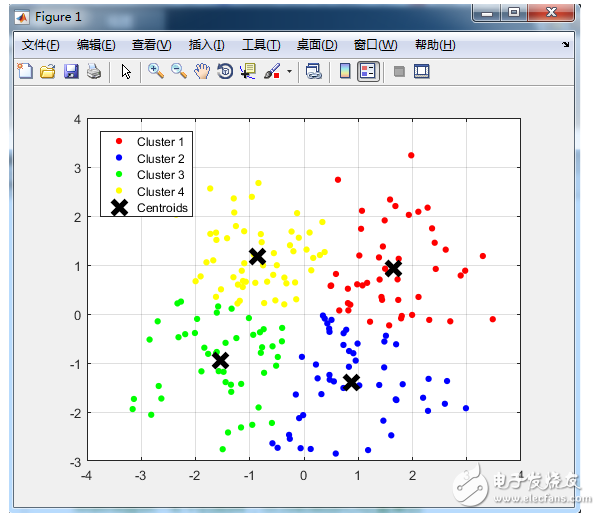
#以Sepal.Length為橫坐標,Sepal.width為縱坐標,畫散點圖,顏色用1,2,3表示缺省顏色
plot(newiris[c(“Sepal.Length”, “Sepal.Width”)], col=class$cluster)
#在散點圖中標出每個類的中心
points(class$centers[,c(“Sepal.Length”, “Sepal.Width”)], col=1:3, pch=8, cex=2)
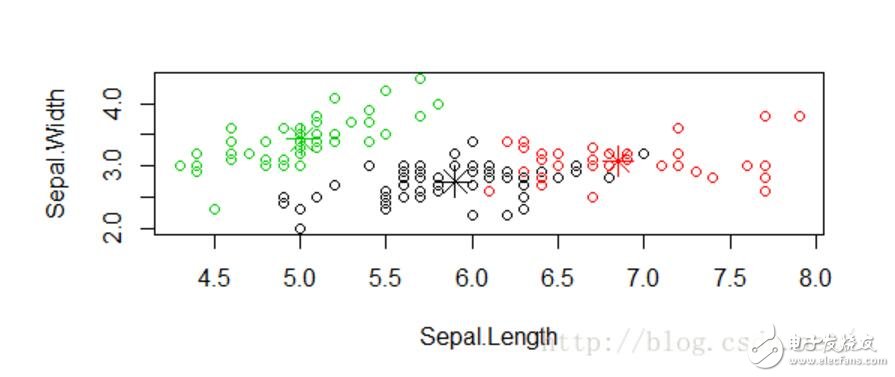
【R語言實現K-means】
原始代碼來自:
http://weibo.com/p/23041875063b660102vi10
[plain] view plain copyMy_kmeans = function(data, k, max.iter=10){
#獲取行,列數
rows = nrow(data)
cols = ncol(data)
#迭代次數
iter = 0
#定義indexMatrix矩陣,第一列為每個數據所在的類,第二列為每個數據到其類中心的距離,初始化為無窮大
indexMatrix = matrix(0, nrow=rows, ncol=2)
indexMatrix[,2] = Inf
#centers矩陣存儲類中心
centers = matrix(0, nrow=k, ncol=cols)
#從樣本中選k個隨機正整數作為初始聚類中心
randSeveralInteger = as.vector(sample(1:rows,size=k))
for(i in 1:k){
indexMatrix[randSeveralInteger[i],1] = i
indexMatrix[randSeveralInteger[i],2] = 0
centers[i,] = as.numeric(data[randSeveralInteger[i],])
}
#changed標記數據所在類是否發生變化
changed=TRUE
while(changed){
if(iter 》= max.iter)
break
changed=FALSE
#對每一個數據,計算其到各個類中心的距離,并將其劃分到距離最近的類
for(i in 1:rows){
#previousCluster表示該數據之前所在類
previousCluster = indexMatrix[i,1]
#遍歷所有的類,將該數據劃分到距離最近的類
for(j in 1:k){
#計算該數據到類j的距離
currentDistance = (sum((data[i,]-centers[j,])^2))^0.5
#如果該數據到類j的距離更近
if(currentDistance 《 indexMatrix[i,2]) {
#認為該數據屬于類j
indexMatrix[i,1] = j
#更新該數據到類中心的距離
indexMatrix[i,2] = currentDistance
}
}
#如果該數據所屬的類發生了變化,則將changed設為TRUE,算法繼續
if(previousCluster != indexMatrix[i,1])
changed=TRUE
}
#重新計算類中心
for(m in 1:k){
clusterMatrix = as.matrix(data[indexMatrix[,1]==m,]) #得到屬于第m個類的所有數據
#如果屬于第m類的數據的數目大于0
if(nrow(clusterMatrix) 》 0){
#更新第m類的類中心
centers[m,] = colMeans(clusterMatrix)
#centers[m,] = apply(clusterMatrix, 2, mean) #兩句效果相同
}
}
iter=(iter+1)#迭代次數+1
}
#計算函數返回值
#cluster返回每個樣本屬于那一類
cluster = indexMatrix[,1]
#center為聚類中心
centers = data.frame(centers)
names(centers) = names(data)
#withinss存儲類內距離平方和
withinss = matrix(0,nrow=k,ncol=1)
ss《-function(x) sum(scale(x,scale=FALSE)^2)
#按照類標號劃分數據集,并對每部分求方差
withinss《-sapply(split(as.data.frame(data),indexMatrix[,1]),ss)
#tot.withinss為類內距離和
tot.withinss《-sum(withinss)
#類間距離
between = ss(centers[indexMatrix[,1],])
size = as.numeric(table(cluster))
#生成返回值列表cluster,tot.withinss,betweenss,iteration
result《-list(cluster=cluster,centers = centers, tot.withinss=withinss,betweenss=between,iter=iter)
return(result)
}
【改進】
1) 選定K的方法
a) 與層次聚類結合。首先采用層次凝聚算法決定結果簇的數目。
b) 設定一些類別分裂和合并的條件,在聚類的過程中自動增減類別的數目,得到較為 合理的類型數目k(ISODATA)
c) 根據方差分析理論(ANOVA),應用混合F統計量確定最佳分類數,應用模糊劃分熵 驗證最佳分類數的正確性;
d) 次勝者受罰的競爭學習規則(RPCL),對每個輸入而言,不僅競爭獲勝單元的權值被 修正以適應輸入值,而且對次勝單元采用懲罰的方法使之遠離輸入值。
2) 選定初始聚類中心
a) 采用遺傳算法初始化
b) 在層次聚類的結果中選取k個類,將這k個類的質心作為初始質心
3) K-means++算法
k-means++算法選擇初始質心的基本思想就是:初始的聚類中心之間的相互距離要盡可能的遠。
a) 從輸入的數據點集合中隨機選擇一個點作為第一個聚類中心
b) 對于數據集中的每一個點x,計算它與最近聚類中心(指已選擇的聚類中心)的 距離D(x)
c) 選擇一個新的數據點作為新的聚類中心,選擇的原則是:D(x)較大的點,被選 取作為聚類中心的概率較大
d) 重復b和c直到k個聚類中心被選出來
e) 利用這k個初始的聚類中心來運行標準的k-means算法
算法的關鍵是第3步,如何將D(x)反映到點被選擇的概率上,一種算法如下:
a) 先從我們的數據庫隨機挑個隨機點當“種子點”
b) 對于每個點,我們都計算其和最近的一個“種子點”的距離D(x)并保存在一個數組 里,然后把這些距離加起來得到Sum(D(x))。
c) 再取一個隨機值,用權重的方式來取計算下一個“種子點”。這個算法的實現 是,先取一個能落在Sum(D(x))中的隨機值Random,然后用Random -= D(x), 直到其《=0,此時的點就是下一個“種子點”。
d) 重復b和c直到k個聚類中心被選出來
e) 利用這k個初始的聚類中心來運行標準的k-means算法
4) 空簇處理
如果所有的點在指派步驟都未分配到某個簇,就會得到空簇。如果這種情況發生,則需要某種策略來選擇一個替補質心,否則的話,平方誤差將會偏大。
a) 一種方法是選擇一個距離當前任何質心最遠的點。這將消除當前對總平方誤差影響最大的點。
b) 另一種方法是從具有最大SSE的簇中選擇一個替補的質心。這將分裂簇并降低聚類的總SSE。如果有多個空簇,則該過程重復多次。
 電子發燒友App
電子發燒友App











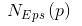










評論