MPU6050模塊,如圖 1所示。該模塊集成了一片MPU6050芯片和一片STM8S003F3P6單片機,具有串口和I2C接口。MPU6050中的DMP(數字運動處理器)對姿態進行融合,STM8單片機通過IIC讀取DMP的處理結果,再添加上包頭串行輸出三軸加速度、三軸角速度、三軸角度和溫度數據,輸出頻率為100Hz。
MPU6050芯片內部由四部分組成:加速度計、陀螺儀、DMP(Digital Motion Processing)、溫度傳感器。DMP部分的Datasheet原文介紹:The DMPacquires data from accelerometers, gyroscopes, and additional 3rdparty sensorssuch as magnetometers, and processes the data. The resulting data can be readfrom the DMP’s registers, or can be buffered in a FIFO. The DMP has access toone of the MPU’s external pins, which can be used for generating interrupts.
陀螺儀誤差分析
imu誤差的效果
陀螺儀的偏移對于速度的影響是二次的,對于位置的影響是三次的。
對于收斂的并且設計很好的濾波器,估計和去除imu的誤差,能夠提高姿態的精度和長期穩定性
常見誤差項:
首先介紹幾個常見的概念:
1.重復性
假設所有的條件一樣,對于相同的輸入,傳感器輸出相同的值的能力(對于每次啟動都相同)。陀螺儀的零偏不具有重復性。
2.穩定性
對于同樣的輸入,在同一次啟動,輸出值都是相同的。
3.漂移
輸出隨著時間的變化(零漂是輸入為0的時候的輸出)
確定性誤差
傳感器非正交性(安裝誤差):
三軸加速度計和陀螺儀的三個軸不是完全的正交的,例如對于加速度計,理想情況下其中一個軸測量重力,其他兩個軸不應該有輸出。傳感器不正交會出現在安裝和封裝的時候。生產和標定能夠一定程度的解決這個問題,在系統運行的時候持續的估計和矯正也是一種解決方法。
尺度誤差(scale)
隨機噪聲
《Notes on Stochastic Errors of Low Cost MEMS Inertial Units》
陀螺儀的噪聲分析不適用arma模型,應該使用allan variance。
因為arma模型假設所有的誤差都是完全客觀的,然而在實際中:傳感器的輸出受到噪聲的影響,而且是不同的獨立隨機過程的和;目前的arma模型能夠解決噪聲的影響,但是不能夠解決獨立隨機過程的系數問題。誤差中最主要的是:(1)零偏、溫漂;(2)角速率噪聲,也叫作隨機游走
所有噪聲可以建模為:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (1)y(t)=u(t)+e(t)+b(T)+N(a,ω,T,t)
(1)y(t)=u(t)+e(t)+b(T)+N(a,ω,T,t)
allan variance 建模
![]()
![]()
![]()
![]() b(T)表示溫漂,一般不考慮,可以通過溫度補償來做
b(T)表示溫漂,一般不考慮,可以通過溫度補償來做
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() N(a,ω,T,t)表示加速度,角速度,溫度和時間等總的因素造成的影響(
N(a,ω,T,t)表示加速度,角速度,溫度和時間等總的因素造成的影響(![]() G 的依賴性(加速度影響),對于mems陀螺儀來說,有可能受到重力的影響,可以通過建模并采用一定的方法去除這個影響)
G 的依賴性(加速度影響),對于mems陀螺儀來說,有可能受到重力的影響,可以通過建模并采用一定的方法去除這個影響)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e(t)=ARW(t)+F(t)+Q(t)+S(t)表示隨機噪聲
e(t)=ARW(t)+F(t)+Q(t)+S(t)表示隨機噪聲
陀螺儀的誤差分類
a。量化噪聲Q(t)(Quantization Noise)
AD采樣導致的噪聲,量化噪聲具有很寬的帶寬,屬于高頻噪聲,可以用低通濾波器處理或通過導航的積分環節去除,對精度的影響不大;
量化噪聲的分辨率為![]() Δ(和AD的位數有關系),采樣頻率為
Δ(和AD的位數有關系),采樣頻率為![]()
![]()
![]()
![]()
![]() f=1/τ(手冊中會介紹采樣的頻率),
f=1/τ(手冊中會介紹采樣的頻率),![]() τ為采樣時間,則量化噪聲的功率譜密度為
τ為采樣時間,則量化噪聲的功率譜密度為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() SΔ(f)=τ0Q2,Allan方差為
SΔ(f)=τ0Q2,Allan方差為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() σQN2(τ)=3Q2τ2。
σQN2(τ)=3Q2τ2。
量化噪聲屬于高頻噪聲,在實際的應用中可進行低通濾波處理或大部分被導航的積分環節濾除。
b。角度隨機游走(ARW(t))(Angular Random Walk)
高斯白噪聲的影響,需要區別角速率輸出還是角增量輸出,mpu6050是角速度輸出。
角度隨機游走的功率譜密度為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() SΩ(f)=N2,Allan方差為
SΩ(f)=N2,Allan方差為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() σARW2(τ)=N2τ
σARW2(τ)=N2τ
一般陀螺儀內部會有低通濾波器。白噪聲功率譜密度的等效帶寬,叫作陀螺儀的帶寬;(慣性儀器,157頁))通過高頻采樣和低通濾波能夠降低mems陀螺儀的角度隨機游走噪聲;
從另外一個角度分析:
假設每次測量的角速度受到白噪聲的影響,即![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() δθk=δθ+Nk?τ,其中
δθk=δθ+Nk?τ,其中![]()
![]() Nk為獨立同分布的零均值白噪聲,標準差
Nk為獨立同分布的零均值白噪聲,標準差![]() σ,則經過時間
σ,則經過時間![]()
![]()
![]() n?τ之后,誤差為
n?τ之后,誤差為
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e=τ∑i=1nNi
e=τ∑i=1nNi
從而![]() e的數學特征為
e的數學特征為![]()
![]()
![]()
![]()
![]()
![]() E(e)=0,
E(e)=0,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Var(e)=δt2nVar(N)=δt?t?σ2
Var(e)=δt2nVar(N)=δt?t?σ2
所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() σ(e)=σ?δt?t
σ(e)=σ?δt?t
因此,在手冊中一般將上面的噪聲常時間的積分的標準差記做
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ARW=σθ(1)
ARW=σθ(1)
單位為![]()
![]()
![]()
![]() °/hc。零偏不穩定性(F(t))(Bias Instability) ,也叫作閃變噪聲(Flicker Noise)
°/hc。零偏不穩定性(F(t))(Bias Instability) ,也叫作閃變噪聲(Flicker Noise)
準確的來說,并不是只有零偏導致偏移,零偏是沒有運動時平均輸出。零偏不穩定性即零偏會隨著時間緩慢的變化。這是由于內部電磁的善變噪聲和外部影響導致的,而且每次啟動之初的零偏是不相同的。
零偏不穩定性的功率譜為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() SΩ(f)=B22πf,Allan方差為
SΩ(f)=B22πf,Allan方差為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() σBI2(τ)=4B29
σBI2(τ)=4B29
零偏的不穩定性描述一段時間之后,MEMS的零偏的變化情況。零偏穩定性通常定義為![]()
![]() 1σ值,單位為
1σ值,單位為![]()
![]()
![]()
![]() °/h。舉例來說,假設當前時刻的零偏是已知的
°/h。舉例來說,假設當前時刻的零偏是已知的![]()
![]() Bt,經過100s后,零偏的均值為
Bt,經過100s后,零偏的均值為![]()
![]() Bt,標準差為
Bt,標準差為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0.01°/h。實際上,零漂并不是一個完全的隨機游走,它的范圍是有限的。零漂對角度的影響是線性的。
0.01°/h。實際上,零漂并不是一個完全的隨機游走,它的范圍是有限的。零漂對角度的影響是線性的。
d。速率斜坡(Rate Ramp)
陀螺的角速率輸出隨著時間緩慢變化,通常由系統誤差引起,比如環境溫度的緩慢變化,可以通過嚴格的環境控制或引入補償來降低此類誤差。這個不應該存在,而且可以通過一定的措施去除掉。貌似就是b(T)溫漂
溫度補償和溫度閉環兩種方法比較:溫度補償很難做,而且效果不好,一般使用溫度閉環;
e。指數相關噪聲(Exponential Correlation Noise)和正弦噪聲![]()
![]()
![]()
![]() S(t)(Sinusoidal Noise)
S(t)(Sinusoidal Noise)
正弦噪聲:由于mems單元在特定頻率工作,所以一般受到正弦噪聲的污染;
從算法上需要解決的:(1)角度隨機游走(2)零偏不穩定性
MPU6050不論是做平衡還是四軸飛行器,關鍵的問題在于模塊姿態的確定,通常需要用到積分運算與卡爾曼濾波算法,需要較強的數學功底與編程能力,因此以下主要分析姿態確定問題。
雖然6050芯片能夠輸出三軸加速度和三軸角速度的數據,但實際應用的時候,直接使用的確不是這些量,而是需要根據這些數據解算出三軸的角度數據。比如平衡小車,需要算出模塊的俯仰角,然后控制算法根據角度大小控制小車輪子的移動。四軸飛行器需要根據俯仰角度、滾轉角度,和飛行指令來調節四個電機的轉速。
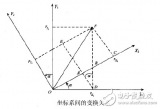
從6軸的原始數據得到三軸的角度計算是一個比較復雜的運動學解算過程,有三點需要注意的問題:
1.三軸姿態的解算不能直接積分。因為三軸是有耦合的,只有在三軸角度為小角度的時候可以這么算,角度大了以后,比如60度了,這么算的誤差就很大。標準的做法是用四元數的方法做姿態解算,積分的方法可以用4階龍格-庫塔法,或者4階Gill法。詳情請參考:航空航天器運動的建模——飛行動力學的理論基礎肖業倫著北京航空航天大學出版社。
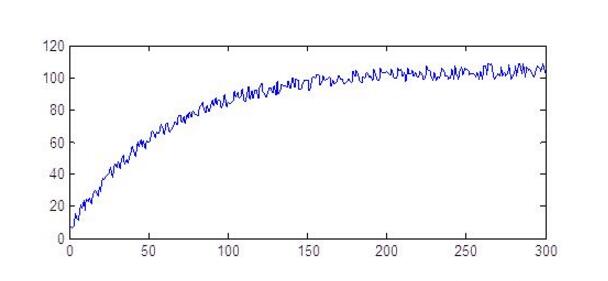
2.積分運算的累積誤差。角速度積分運算是有累積誤差的,累積誤差在短時間內表現不明顯,只要零點漂移處理得好了,1分鐘以內的漂移都不大,但時間長了,就會有累積誤差。穩像儀中使用的MPU6050模塊零點漂移比較小,5分鐘大概0.02度。
3.角速率零點漂移。所謂零點漂移就是模塊靜止的時候,我們認為正常的輸出應該是0,或者均值為0的數據,但是實際上6050的輸出不是,經測量,小于0.15度/秒。
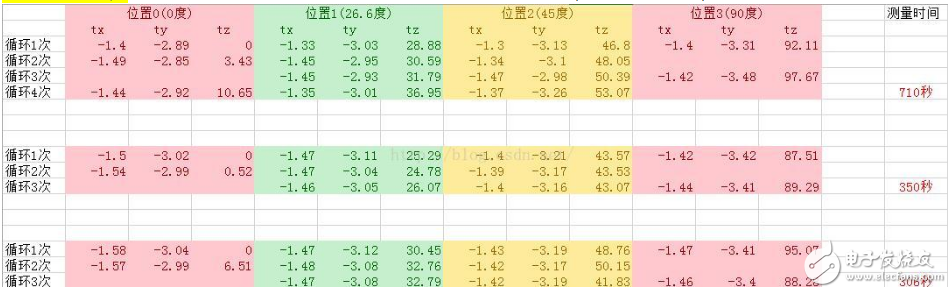
在紙上畫出四個角度,分別為0度、26.6度、45度、90度,將紙固定在桌子上,每次將陀螺儀模塊旋轉到對應的位置,經過多次實驗(實驗結果如圖2所示),證實所使用的MPU6050模塊的角度輸出確實存在很大的誤差。但是從datasheet上看,MPU6050芯片和其他精度高且價格昂貴的芯片如ADIS16系列差別不是大,那么極有可能是姿態融合算法部分的問題。MPU6050模塊的姿態融合是在STM8單片機中實現的,而且沒有源碼,精度難以保證。
綜上所述,有兩種解決方法:
一、使用MPU6050模塊輸出的角速度和加速度的原始數據,用算法對其進行姿態融合,得到角度。綜合利用陀螺儀和加速度計的特點,優勢互補獲得準確的姿態角度,方法就是用卡爾曼濾波做數據融合。大致的思路是將模塊的姿態用四元素表示,作為系統的狀態量,模塊的姿態運動學方程作為濾波的狀態轉移方程,加速度信息作為濾波的觀察量信息,然后利用卡爾曼濾波的計算方法迭代計算更新,詳細的過程可以參考慣性導航方面的書籍。不過卡爾曼濾波算法比較復雜,需要用到矩陣運算等等,而且MPU6050模塊是IIC接口輸出的。
二、采用更高精度的陀螺儀模塊,直接得到角度。
 電子發燒友App
電子發燒友App



















評論