BCD碼(Binary-Coded Decimal?)亦稱二進碼十進數或二-十進制代碼。用4位二進制數來表示1位十進制數中的0~9這10個數碼。是一種二進制的數字編碼形式,用二進制編碼的十進制代碼。BCD碼這種編碼形式利用了四個位元來儲存一個十進制的數碼,使二進制和十進制之間的轉換得以快捷的進行。
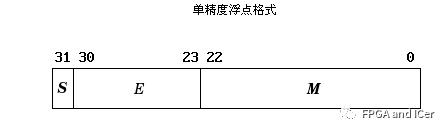
這種編碼技巧最常用于會計系統的設計里,因為會計制度經常需要對很長的數字串作準確的計算。相對于一般的浮點式記數法,采用BCD碼,既可保存數值的精確度,又可免去使電腦作浮點運算時所耗費的時間。此外,對于其他需要高精確度的計算,BCD編碼亦很常用。
由于十進制數共有0、1、2、……、9十個數碼,因此,至少需要4位二進制碼來表示1位十進制數。4位二進制碼共有2^4=16種碼組,在這16種代碼中,可以任選10種來表示10個十進制數碼,共有N=16!/[10!*(16-10)!]等于8008種方案。常用的BCD代碼列于末。
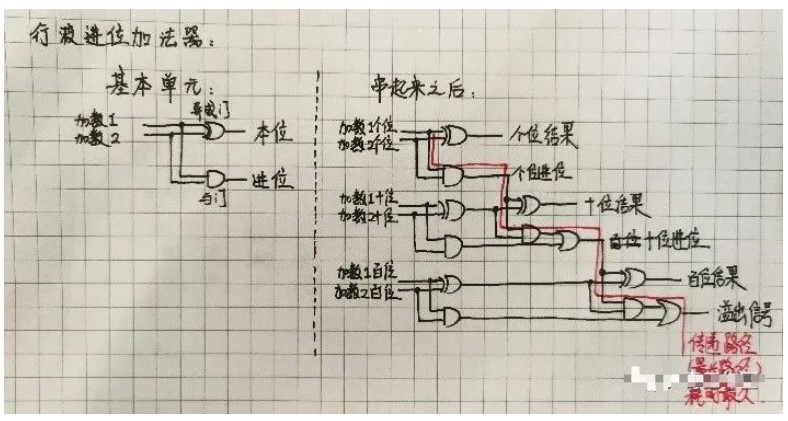
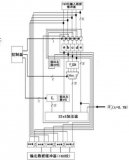
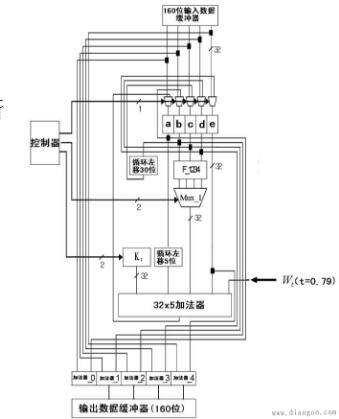
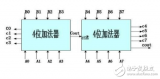
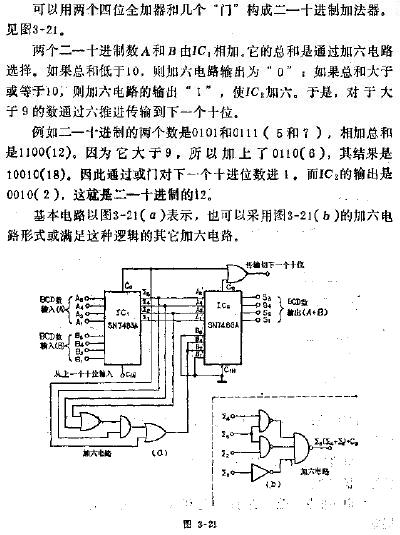
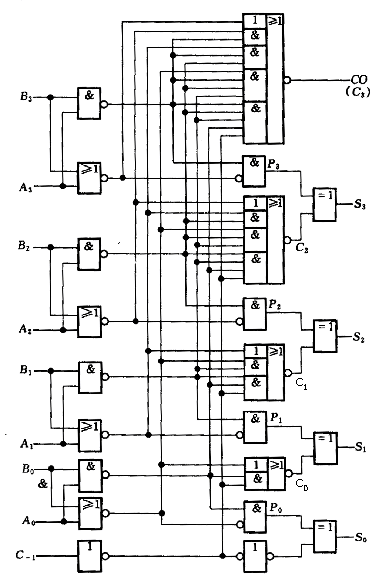
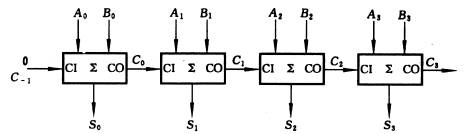
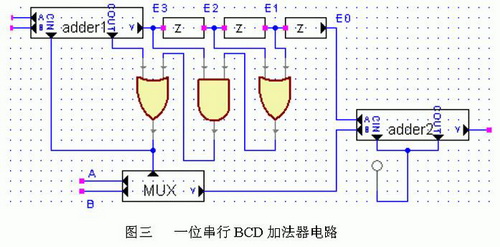
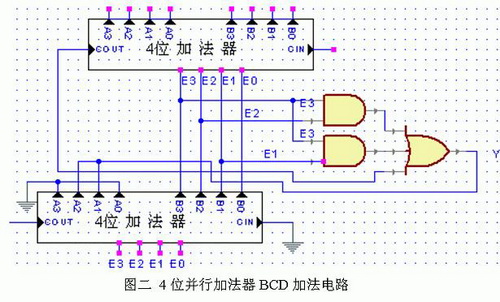
BCD碼加法器
在計算機內部,出于存儲和計算方便的目的,采用基2碼對十進制數進行重新編碼,最少需要基2碼的位數為log210,取整數位4 ,4位基2碼有16種表示方法。
十進制數的幾種4位編碼
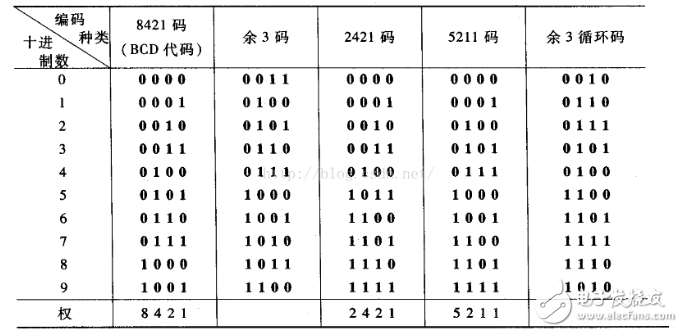
8421碼又稱BCD碼,是十進制代碼中最常用的一種。在這種編碼方式中,每一位二值代碼的1都表示一個固定數值,將每一位的1代表的十進制數加起來,得到的結果就是它所代表的十進制數碼。由于代碼中從左到右每一位的1分別表示8、4、2、1,所以將這種編碼稱為8421碼。每一位的1代表的十進制數稱為這一位的權。8421碼中每一位的權是固定不變的,它屬于恒權代碼。
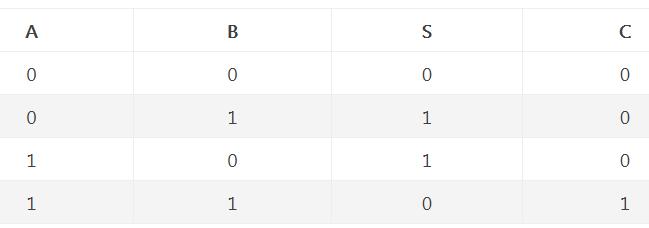
在計算機內部實現BCD碼之間的算術運算要復雜一些,即在某些情況下,對加法運算的結果進行修正。修正規則如下:
(1) 若兩個8421碼數相加之和等于或小于1001,不需修正。
(2) 若相加和在10-15之間,一方面應向高位產生進位,本身還要進行加6修正,進位是在加6修正時產生的。
(3) 若相加之和在16-18之間,向高位進位會在相加過程中自己產生,對本位還要進行加6修正。
實驗代碼使用vhdl語言:
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
ENTITY bcd IS
PORT( a : UNSIGNED(4 DOWNTO 0);
b : UNSIGNED(4 DOWNTO 0);
c : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)
);
END bcd;
SIGNAL sum : STD_LOGIC_VECTOR(4 DOWNTO 0);
SIGNAL co : STD_LOGIC;
SIGNAL add : integer RANGE 0 TO 31;
BEGIN
add 《= conv_integer(a+b);
co 《= ‘1’ WHEN add》9 ELSE
‘0’;
sum 《= a+b+6 WHEN co=‘1’ ELSE
a+b;
c 《= sum;
END adding;
 電子發燒友App
電子發燒友App










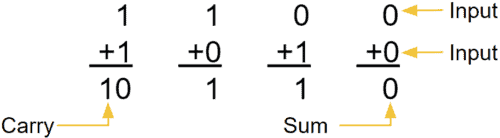














評論