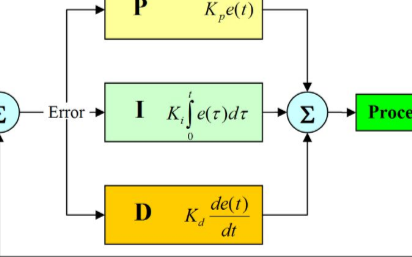
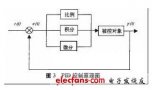
在過程控制中,按偏差的比例(P)、積分(I)和微分(D)進行控制的PID控制器(亦稱PID調節器)是應用最為廣泛的一種自動控制器。它具有原理簡單,易于實現,適用面廣,控制參數相互獨立,參數的選定比較簡單等優點;而且在理論上可以證明,對于過程控制的典型對象──“一階滯后+純滯后”與“二階滯后+純滯后”的控制對象,PID控制器是一種最優控制。PID調節規律是連續系統動態品質校正的一種有效方法,它的參數整定方式簡便,結構改變靈活(PI、PD、…)。
控制點包含三種比較簡單的PID控制算法,分別是:增量式算法,位置式算法,微分先行。 這三種PID算法雖然簡單,但各有特點,基本上能滿足一般控制的大多數要求。
PID算法簡介
在智能車競賽中,要想讓智能車根據賽道的不斷變化靈活的行進,PID算法的采用很有意義。
首先必須明確PID算法是基于反饋的。一般情況下,這個反饋就是速度傳感器返回給單片機當前電機的轉速。簡單的說,就是用這個反饋跟預設值進行比較,如果轉速偏大,就減小電機兩端的電壓;相反,則增加電機兩端的電壓。
顧名思義,P指是比例(Proportion),I指是積分(Integral),D指微分(Differential)。在電機調速系統中,輸入信號為正,要求電機正轉時,反饋信號也為正(PID算法時,誤差=輸入-反饋),同時電機轉速越高,反饋信號越大。要想搞懂PID算法的原理,首先必須先明白P,I,D各自的含義及控制規律:
2 比例P:比例項部分其實就是對預設值和反饋值差值的發大倍數。舉個例子,假如原來電機兩端的電壓為U0,比例P為0.2,輸入值是800,而反饋值是1000,那么輸出到電機兩端的電壓應變為U0+0.2*(800-1000)。從而達到了調節速度的目的。顯然比例P越大時,電機轉速回歸到輸入值的速度將更快,及調節靈敏度就越高。從而,加大P值,可以減少從非穩態到穩態的時間。但是同時也可能造成電機轉速在預設值附近振蕩的情形,所以又引入積分I解決此問題。
比例控制理解
首先是比例控制。比例控制就好比是通過水桶往水缸加水或者從水缸舀水。假設我們需要把水平面穩定在A平面,而實際水平面在B平面,那么水平面差值Err=A-B,那這個時候我們需要往里面加水的量就是Kp*Err,Kp就是我們的比例控制系數。
如果A》B,Err為正,就往水缸里面加水;如果A《B,Err為負,就從水缸里面舀水出來。那么只要預期水平面和實際水平面有差值,我們都會通過水桶去加減水來調整系統。同時Kp的大小也有對系統的性能有影響。如果Kp的值比較大,優點是從B平面達到A平面的速度快,缺點是在B平面已經接近A平面的時候系統會產生比較大的震蕩。如果Kp的值比較小,優點是B平面在接近A平面的時候系統震蕩小,缺點是從B平面達到A平面的速度慢。
這里也許有人會有疑問,如果這里把比例控制系數Kp直接設置成1,然后加水的量直接為Err=A-B不就可以了。然而實際上很多系統是做不到這點的。比如溫度控制系統,實際溫度為10度,我要通過加熱把溫度提升到40度,這里難道我們能一次性準確的給系統加30度?顯然這是做不到的。那么比例控制的最終結果是Err的值趨向于0。比例控制部分公式如下圖:
2 積分I:顧名思義,積分項部分其實就是對預設值和反饋值之間的差值在時間上進行累加。當差值不是很大時,為了不引起振蕩。可以先讓電機按原轉速繼續運行。當時要將這個差值用積分項累加。當這個和累加到一定值時,再一次性進行處理。從而避免了振蕩現象的發生。可見,積分項的調節存在明顯的滯后。而且I值越大,滯后效果越明顯。
積分控制理解
積分控制部分的作用主要是用來消除靜差。那么積分是怎樣來消除靜差的呢?
比例控制只能盡量將Err調節到0,而微分的作用是將曲線的斜率控制到0則停止對其作用,但斜率為0的時候Err并不一定為0。
這個時候我們就需要積分來起作用了。我們知道曲線的積分相當于曲線與x軸圍出來的面積。如下圖,積分作用的目的是使紅色部分的面積和藍色部分的面積的和為0,那么即使系統在比例控制和微分控制部分已經趨于穩定,只要Err不為0就會存在靜差,只要存在靜差那么積分就會對系統產生影響,直到系統的Err值為0。那么這樣我們的PID控制在理論上就可以達到一個非常精確的控制效果。
來看看我們的積分公式部分:
2 微分D:微分項部分其實就是求電機轉速的變化率。也就是前后兩次差值的差而已。也就是說,微分項是根據差值變化的速率,提前給出一個相應的調節動作。可見微分項的調節是超前的。并且D值越大,超前作用越明顯。可以在一定程度上緩沖振蕩。比例項的作用僅是放大誤差的幅值,而目前需要增加的是“微分項”,它能預測誤差變化的趨勢,這樣,具有比例+微分的控制器,就能夠提前使抑制誤差的控制作用等于零,甚至為負值,從而避免了被控量的嚴重超調。
微分控制理解
然后我們先看看微分控制。在我們的比例控制的作用下,Err是開始減小的(假設一開始預期水平面A大于實際水平面B,也就是說Err是一個正值),那么也就是說Err隨時間是一條斜率小于0的曲線,那么在周期時間內,Err越大,微分的絕對值越大,那么也就對Err的減小速度是起到抑制的作用的,直到最后斜率為0微分才會停止作用。微分公式如下:
那么隨著微分的影響,Err曲線的斜率最終是趨向于0的,如下圖:
二、參數調整一般規則
由各個參數的控制規律可知,比例P使反應變快,微分D使反應提前,積分I使反應滯后。在一定范圍內,P,D值越大,調節的效果越好。各個參數的調節原則如下:
PID調試一般原則
a. 在輸出不振蕩時,增大比例增益P。
b. 在輸出不振蕩時,減小積分時間常數Ti。
c. 輸出不振蕩時,增大微分時間常數Td。
三、參數調整一般步驟
a.確定比例增益P
確定比例增益P 時,首先去掉PID的積分項和微分項,一般是令Ti=0、Td=0,PID為純比例調節。輸入設定為系統允許的最大值的60%~70%,由0逐漸加大比例增益P,直至系統出現振蕩;再反過來,從此時的比例增益P逐漸減小,直至系統振蕩消失,記錄此時的比例增益P,設定PID的比例增益P為當前值的60%~70%。比例增益P調試完成。
b.確定積分時間常數Ti
比例增益P確定后,設定一個較大的積分時間常數Ti的初值,然后逐漸減小Ti,直至系統出現振蕩,之后在反過來,逐漸加大Ti,直至系統振蕩消失。記錄此時的Ti,設定PID的積分時間常數Ti為當前值的150%~180%。積分時間常數Ti調試完成。
c.確定積分時間常數Td
積分時間常數Td一般不用設定,為0即可。若要設定,與確定 P和Ti的方法相同,取不振蕩時的30%。
d.系統空載、帶載聯調,再對PID參數進行微調,直至滿足要求
找三個以上PID算法應用實例,結合實例明確參數調試的方法以及參數的意義,同時給小組成員做介紹
 電子發燒友App
電子發燒友App








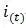
















評論