五、PID算法原理

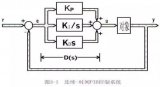
　　在工業應用中PID及其衍生算法是應用最廣泛的算法之一，是當之無愧的萬能算法，如果能夠熟練掌握PID算法的設計與實現過程，對于一般的研發人員來講，應該是足夠應對一般研發問題了，而難能可貴的是，在我所接觸的控制算法當中，PID控制算法又是最簡單，最能體現反饋思想的控制算法，可謂經典中的經典。經典的未必是復雜的，經典的東西常常是簡單的，而且是最簡單的，想想牛頓的力學三大定律吧，想想愛因斯坦的質能方程吧，何等的簡單！簡單的不是原始的，簡單的也不是落后的，簡單到了美的程度。先看看PID算法的一般形式：

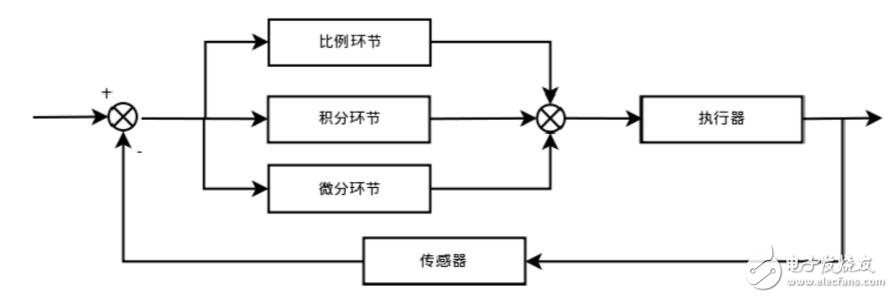
　　PID的流程簡單到了不能再簡單的程度，通過誤差信號控制被控量，而控制器本身就是比例、積分、微分三個環節的加和。這里我們規定（在t時刻）：

　　1.輸入量為rin（t）;

　　2.輸出量為rout（t）;

　　3.偏差量為err（t）=rin（t）-rout（t）;

　　pid的控制規律為

　　理解一下這個公式，主要從下面幾個問題著手，為了便于理解，把控制環境具體一下：

　　1.規定這個流程是用來為直流電機調速的;

　　2.輸入量rin（t）為電機轉速預定值;

　　3.輸出量rout（t）為電機轉速實際值

　　4.執行器為直流電機;

　　5.傳感器為光電碼盤，假設碼盤為10線;

　　6.直流電機采用PWM調速轉速用單位轉/min表示;不難看出以下結論：

　　1.輸入量rin（t）為電機轉速預定值（轉/min）;2.輸出量rout（t）為電機轉速實際值（轉/min）;3.偏差量為預定值和實際值之差（轉/min）

　　六、PID算法應用——線性控制原理

　　PID控制的三要素：控制器，被控對象，反饋器。控制器就是一個數學模型，就PID來說，等同于PID算法。是對反饋量的一個處理與輸出。通俗的說就是對于每個被控的量，我的輸出量通過什么函數式算出，或者說，我如何描述我的輸出量。現在我給定一個描述性的傳遞函數。從數學角度來看：它的自變量是反饋值，當這個函數的對應關系確定了之后，輸出量就是個定值了。我的希望是：這個描述函數是一個透明的空箱——它既能反映系統外部特性，又可以看到其內部結構。

　　就拿比賽來說：假設我現在要構建這樣一個閉環系統，這個系統的反饋調節建立了一個描述函數，最根本的在于：

　　1 這個系統的動態性從根本上講取決于哪些因素；2這些因素如何決定系統的性能；

　　數學模型的描述：1 描述函數-》微分方程。描述函數的自變量與因變量滿足微分方程。（瞬間變化的關系式）

　　2 將微分方程做一個處理，得出其特征方程，這個特征方程稱作描述函數的極點。

　　ps：下面簡述一下極點和零點。對描述函數做拉普拉斯變換，將描述函數變換成一個與它本身相關的函數，并找出其通解和特解，通解是這個函數的開環特征，用來描述輸出與輸入的關系，零點是調節變量，用于閉環中對系統反饋參數的調節。（對函數做拉普拉斯變換事實上是針對描述大多函數是常微分方程的一種現象）

　　我們有必要對這個描述函數的解進行研究，盡管在線性控制原理中并不關注并不要求去了解他，但是對于這個常微分方程的極點形式的了解有助于我們認識這個描述函數的物理意義。這是高數的知識，就不再累述。通過求解，可以看到極點其實就是這個經過拉普拉斯變換的描述函數的一次項的系數，零點是反饋量的相關函數的系數。也就是說，極點一旦確定，這個函數也就確定了，對于每一個輸入函數，賦予零點變換，再進過極點變換 ，最后生成輸出量。

　　把我們現在得到的結論聯系一下：對于一個閉環的系統我們通過對控制器一些參數的理論求解，或者說調試求解，最終改變輸出變量，從而使這個系統持續穩定。也就是說，在控制器內，存儲了有關于反饋值某種預期的實現方法，這些方法用一些固定的參數來描述，然后輸出變量改變系統的狀態。我的任務是調試這些具有物理意義的參數。

　　下面是一個簡單的PID程序設計：

　　double kp，ki，kd;

　　double resultfunc（void）

　　{

　　double error;

　　double diff;

　　double lasterror = 0;

　　error = target - input;

　　sumerror += error;

　　diff = error - lasterror;

　　lasterror = error;

　　output = kp * error + ki * sumerror + kd * diff;

　　return output;

　　}

　　你會發現其實想象中的PID要比現實中的PID復雜很多，這是理所當然的，因為經過PID數學計算之后，帶入的公式只是一個近似量。但是這可不是隨便瞎設的一個值，最重要的是，你需要數學計算。

　　不得不說一下，對于一個完全的門外漢來說，PID是一個十分高神的名詞，很多人一上手就接觸PID，結果連輸出輸入的到底是什么都搞不明白，其實不妨接觸一下線性控制的理論，這對于你的視野和思路有及其清晰的指導。

　　參數整定尋最佳，從小到大順序查；

　　先是比例后積分，最后才把微分加；

　　曲線振蕩很頻繁，比例度盤要放大；

　　曲線漂浮繞大彎，比例度盤往小扳；

　　曲線偏離回復慢，積分時間往下降；

　　曲線波動周期長，積分時間再加長；

　　曲線振蕩變很快，先把微分降下來；

　　動差大來波動慢，微分時間要加長；

　　聯想曲線兩個波，前高后低4比1；

　　一看二調多分析，調節質量不會低。