一、最短路徑簡介
用于計算一個節(jié)點到其他所有節(jié)點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優(yōu)解,但由于它遍歷計算的節(jié)點很多,所以效率低。
二、動態(tài)規(guī)劃求解問題的思路
在《算法導(dǎo)論》上,動態(tài)規(guī)劃的求解過程主要分為如下的四步:
描述最優(yōu)解的結(jié)構(gòu)
遞歸定義最優(yōu)解的值
按自底向上的方式計算最優(yōu)解的值
由計算出的結(jié)果構(gòu)造一個最優(yōu)解
在利用動態(tài)規(guī)劃求解的過程中值得注意的就是是否包含最優(yōu)子結(jié)構(gòu),簡單來講就是一個問題的最優(yōu)解是不是包含著子問題的最優(yōu)解。利用求解子問題的最優(yōu)解最后得到整個問題的最優(yōu)解,這是利用動態(tài)規(guī)劃求解問題的基本前提。
三、利用動態(tài)規(guī)劃求解最短路徑問題
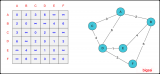
在解決這個問題的過程中,我其實是在嘗試著使用不同的工具,首先我想對這種圖處理,我使用了Gephi,Gephi是我在學(xué)習(xí)復(fù)雜網(wǎng)絡(luò)的時候?qū)W會的一個工具,這個工具可以很方便的處理網(wǎng)絡(luò)數(shù)據(jù),能夠動態(tài)的生成圖的結(jié)構(gòu),下面是我用Gephi畫出的圖:
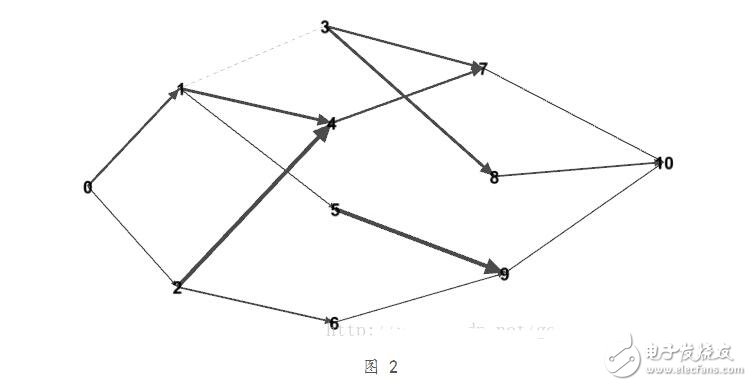
Gephi的另一個比較重要的工具就是可以在生成圖的過程中,將圖的數(shù)據(jù)導(dǎo)出,導(dǎo)出的數(shù)據(jù)可以方便的使用。
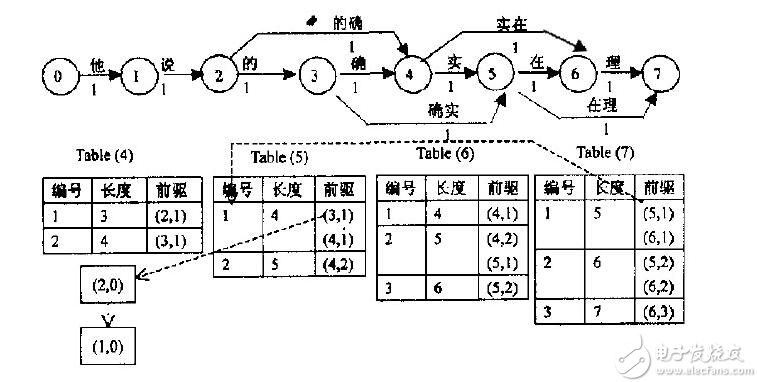
還是重點說說我是怎么利用動態(tài)規(guī)劃的思想去求解這樣的最短路徑問題的:
1、描述最優(yōu)解的結(jié)構(gòu)
要使得從0到10的距離最短,令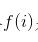 為到第個節(jié)點的最短距離,則
為到第個節(jié)點的最短距離,則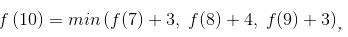 用同樣的方法可以求得
用同樣的方法可以求得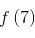 等。
等。
2、遞歸定義最優(yōu)解的值
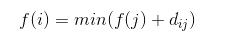
其中表示與邊有連接的節(jié)點,而且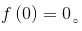 。
。
3、按自底向上的方式計算每個節(jié)點的最優(yōu)值
此時我們就得利用遞歸公式分別求解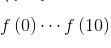 ,這樣最終便能得到最終的解。
,這樣最終便能得到最終的解。
結(jié)果為:
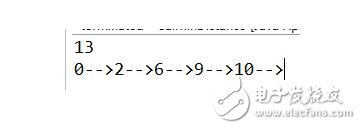
最短路徑解決方法
用于解決最短路徑問題的算法被稱做“最短路徑算法”, 有時被簡稱作“路徑算法”。 最常用的路徑算法有:
Dijkstra算法
SPFA算法\Bellman-Ford算法
Floyd算法\Floyd-Warshall算法
Johnson算法
A*算法
所謂單源最短路徑問題是指:已知圖G=(V,E),我們希望找出從某給定的源結(jié)點S∈V到V中的每個結(jié)點的最短路徑。
?
首先,我們可以發(fā)現(xiàn)有這樣一個事實:如果P是G中從vs到vj的最短路,vi是P中的一個點,那么,從vs沿P到vi的路是從vs到vi的最短路。
JAVA實現(xiàn):
[java] view plain copypackage org.algorithm.dynamicprogramming;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.IOException;
import java.io.Reader;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
import java.util.Stack;
/**
* 利用動態(tài)規(guī)劃求解最短路徑問題
*
* @author dell
*
*/
public class CalMinDistance {
// 計算最短的距離
public static int[] calMinDistance(int distance[][]) {
int dist[] = new int[distance.length];
dist[0] = 0;
for (int i = 1; i 《 distance.length; i++) {
int k = Integer.MAX_VALUE;
for (int j = 0; j 《 i; j++) {
if (distance[j][i] != 0) {
if ((dist[j] + distance[j][i]) 《 k) {
k = dist[j] + distance[j][i];
}
}
}
dist[i] = k;
}
return dist;
}
// 計算路徑
public static String calTheRoute(int distance[][], int dist[]) {
Stack《Integer》 st = new Stack《Integer》();
StringBuffer buf = new StringBuffer();
int j = distance.length - 1;
st.add(j);// 將尾插入
while (j 》 0) {
// int num = 0;
for (int i = 0; i 《 j; i++) {
if (distance[i][j] != 0) {
// num++;
if (dist[j] - distance[i][j] == dist[i]) {
st.add(i);
}
}
}
j = st.peek();
}
while (!st.empty()) {
buf.append(st.pop()).append(“--》”);
}
return buf.toString();
}
// 讀取文件
@SuppressWarnings(“resource”)
public static int[][] readTheFile(File f) {
Reader input = null;
try {
input = new FileReader(f);
} catch (FileNotFoundException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
BufferedReader buf = null;
buf = new BufferedReader(input);
List《String》 list = new ArrayList《String》();
try {
String str = buf.readLine();
while (str != null) {
list.add(str);
str = buf.readLine();
}
} catch (IOException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
Iterator《String》 it = list.iterator();
int distance[][] = new int[11][11];
while (it.hasNext()) {
String str1[] = it.next().split(“,”);
int i = Integer.parseInt(str1[0]);
int j = Integer.parseInt(str1[1]);
distance[i - 1][j - 1] = Integer.parseInt(str1[2]);
}
return distance;
}
public static void main(String args[]) {
// 讀文件
File f = new File(“D:” + File.separator + “distance_1.csv”);
int distance[][] = readTheFile(f);
int dist[] = calMinDistance(distance);
System.out.println(“最短路徑長度為:” + dist[distance.length - 1]);
System.out.println(“最短路徑為:” + calTheRoute(distance, dist));
}
}
?
 電子發(fā)燒友App
電子發(fā)燒友App


















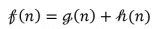












評論