貝葉斯分類器的分類原理是通過某對象的先驗概率，利用貝葉斯公式計算出其后驗概率，即該對象屬于某一類的概率，選擇具有最大后驗概率的類作為該對象所屬的類。

　　種類

　　貝葉斯分類器的分類原理是通過某對象的先驗概率，利用貝葉斯公式計算出其后驗概率，即該對象屬于某一類的概率，選擇具有最大后驗概率的類作為該對象所屬的類。也就是說，貝葉斯分類器是最小錯誤率意義上的優化。目前研究較多的貝葉斯分類器主要有四種，分別是：Naive Bayes、TAN、BAN和GBN。

　　解釋

　　貝葉斯網絡是一個帶有概率注釋的有向無環圖，圖中的每一個結點均表示一個隨機變量，圖中兩結點間若存在著一條弧，則表示這兩結點相對應的隨機變量是概率相依的，反之則說明這兩個隨機變量是條件獨立的。網絡中任意一個結點X 均有一個相應的條件概率表（Conditional Probability Table，CPT），用以表示結點X 在其父結點取各可能值時的條件概率。若結點X 無父結點，則X 的CPT 為其先驗概率分布。貝葉斯網絡的結構及各結點的CPT 定義了網絡中各變量的概率分布。

　　一、分類器的基本概念

　　經過了一個階段的模式識別學習，對于模式和模式類的概念有一個基本的了解，并嘗試使用MATLAB實現一些模式類的生成。而接下來如何對這些模式進行分類成為了學習的第二個重點。這就需要用到分類器。

　　表述模式分類器的方式有很多種，其中用的最多的是一種判別函數gi（x），i=1，2.。。，c的形式，如果對于所有的j≠i，有：gi（x）》g（x）

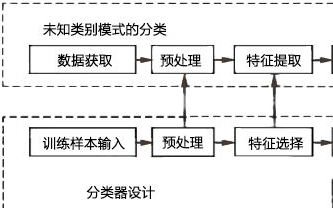
　　則此分類器將這個特征向量x判為ωi類。因此，此分類器可視為計算c個判別函數并選取與最大判別值對應的類別的網絡或機器。一種分類器的網絡結構如下圖所示：

　　

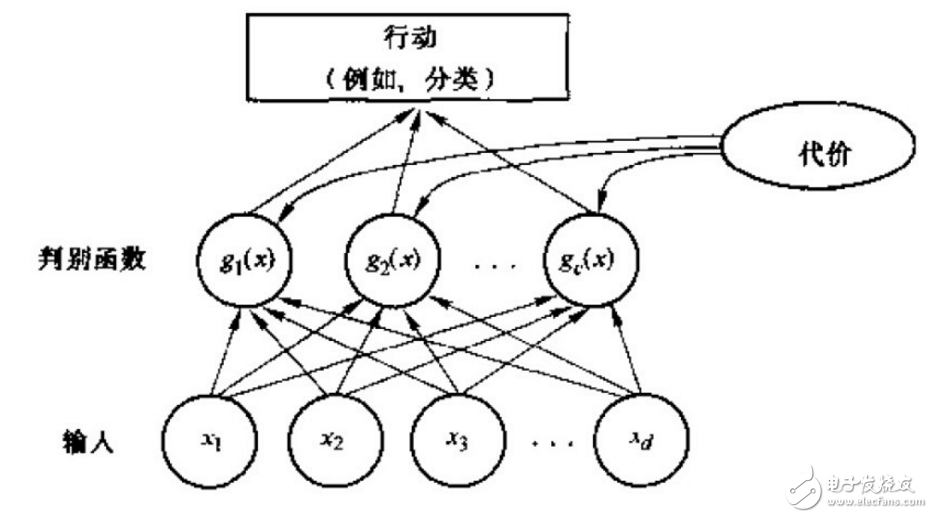
　　二、貝葉斯分類器

　　一個貝葉斯分類器可以簡單自然地表示成以上網絡結構。貝葉斯分類器的分類原理是通過某對象的先驗概率，利用貝葉斯公式計算出其后驗概率，即該對象屬于某一類的概率，選擇具有最大后驗概率的類作為該對象所屬的類。在具有模式的完整統計知識條件下，按照貝葉斯決策理論進行設計的一種最優分類器。分類器是對每一個輸入模式賦予一個類別名稱的軟件或硬件裝置，而貝葉斯分類器是各種分類器中分類錯誤概率最小或者在預先給定代價的情況下平均風險最小的分類器。它的設計方法是一種最基本的統計分類方法。

　　對于貝葉斯分類器，其判別函數的選擇并不是唯一的，我們可以將所有的判別函數乘上相同的正常數或者加上一個相同的常量而不影響其判決結果；在更一般的情況下，如果將每一個gi （x）替換成f（gi （x）），其中f（?）是一個單調遞增函數，其分類的效果不變。特別在對于最小誤差率分類，選擇下列任何一種函數都可以得到相同的分類結果，但是其中一些比另一些計算更為簡便：

　　

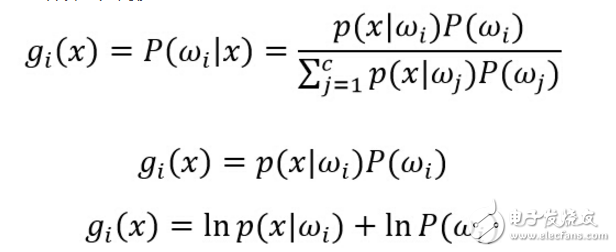
　　一個典型的模式識別系統是由特征提取和模式分類兩個階段組成的，而其中模式分類器（Classifier）的性能直接影響整個識別系統的性能。 因此有必要探討一下如何評價分類器的性能，這是一個長期探索的過程。分類器性能評價方法見：http://blog.csdn.net/liyuefeilong/article/details/44604001

　　三、基本的Bayes分類器實現

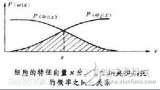
　　這里將在MATLAB中實現一個可以對兩類模式樣本進行分類的貝葉斯分類器，假設兩個模式類的分布均為高斯分布。模式類1的均值矢量m1 = （1， 3），協方差矩陣為S1 =（1.5， 0; 0， 1）；模式類2的均值矢量m2 = （3， 1），協方差矩陣為S2 =（1， 0.5; 0.5， 2），兩類的先驗概率p1 = p2 = 1/2。詳細的操作包含以下四個部分：

　　1.首先，編寫一個函數，其功能是為若干個模式類生成指定數目的隨機樣本，這里為兩個模式類各生成100個隨機樣本，并在一幅圖中畫出這些樣本的二維散點圖；

　　

　　2.由于每個隨機樣本均含有兩個特征分量，這里先僅僅使用模式集合的其中一個特征分量作為分類特征，對第一步中的200個樣本進行分類，統計正確分類的百分比，并在二維圖上用不同的顏色畫出正確分類和錯分的樣本；（注：綠色點代表生成第一類的散點，紅色代表第二類；綠色圓圈代表被分到第一類的散點，紅色代表被分到第二類的散點！ 因此，里外顏色不一樣的點即被錯分的樣本。）

　　

　　3.僅用模式的第二個特征分量作為分類特征，重復第二步的操作；

　　

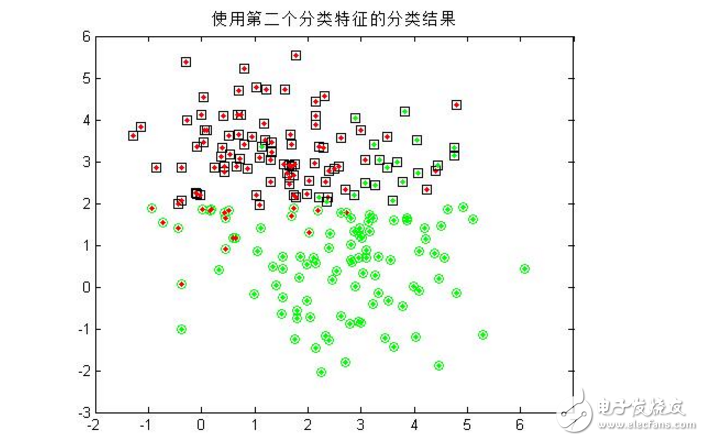
　　4.同時用模式的兩個分量作為分類特征，對200個樣本進行分類，統計正確分類百分比，并在二維圖上用不同的顏色畫出正確分類和錯分的樣本；

　　

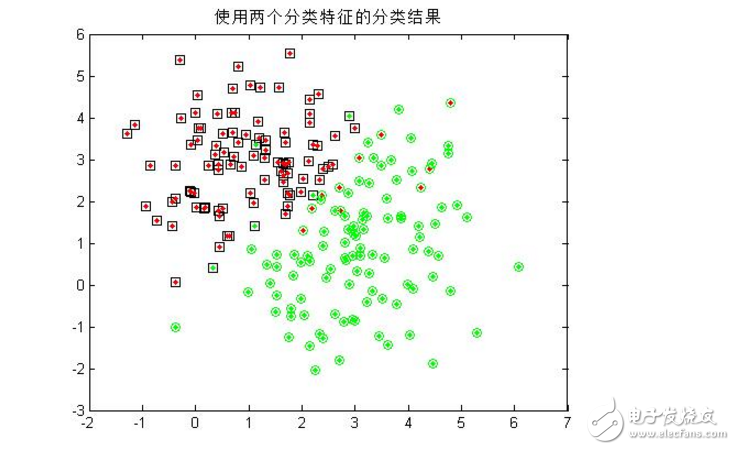
　　正確率：

　　

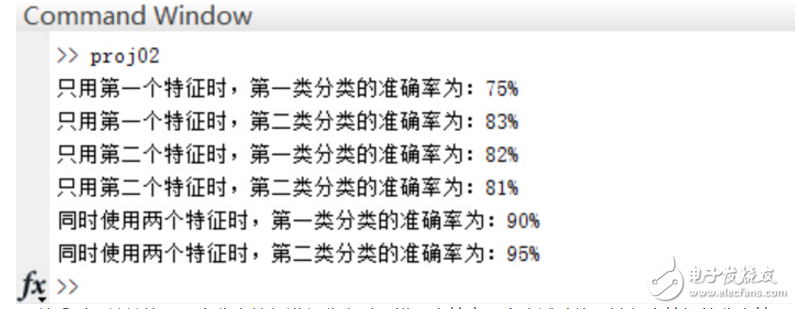
　　可以看到，單單使用一個分類特征進行分類時，錯誤率較高（多次試驗均無法得出較好的分類結果），而增加分類特征的個數是提高正確率的有效手段，當然，這會給算法帶來額外的時間代價。

　　四、進一步的Bayes分類器

　　假設分類數據均滿足高斯分布的情況下，設計一個判別分類器，實驗目的是為了初步了解和設計一個分類器。

　　1.編寫一個高斯型的Bayes判別函數GuassianBayesModel（ mu，sigma，p，X ），該函數輸入為：一給定正態分布的均值mu、協方差矩陣sigma，先驗概率p以及模式樣本矢量X，輸出判別函數的值，其代碼如下：

　　2.以下表格給出了三類樣本各10個樣本點，假設每一類均為正態分布，三個類別的先驗概率相等均為P（w1）=P（w2 ）=P（w3 ）=1/3。計算每一類樣本的均值矢量和協方差矩陣，為這三個類別設計一個分類器。

　　

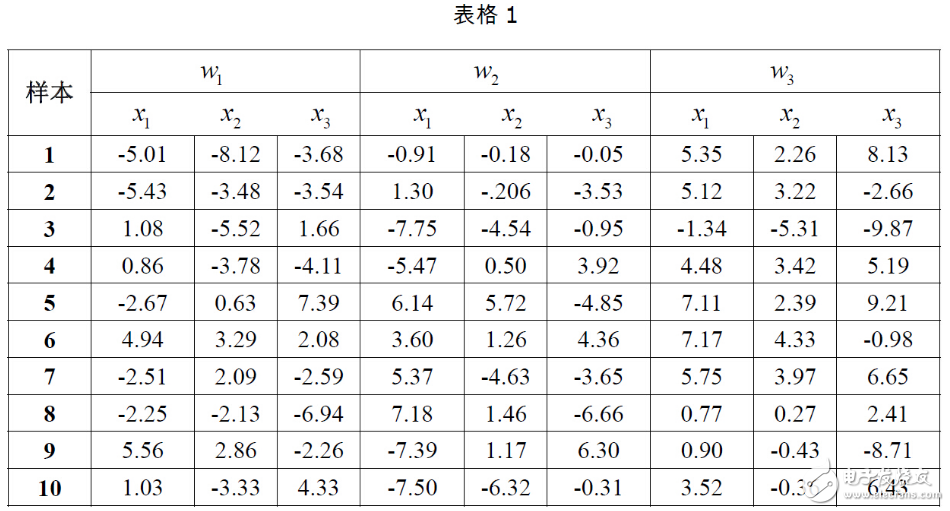
　　3.用第二步中設計的分類器對以下測試點進行分類：（1，2，1），（5，3，2），（0，0，0），并且利用以下公式求出各個測試點與各個類別均值之間的Mahalanobis距離。以下是來自百度百科的關于馬氏距離的解釋：

　　

　　馬氏距離計算公式：

　　

　　更具體的見： http://baike.baidu.com/link？url=Pcos75ou28q7IukueePCNqf8N7xZifuXOTrwzeWpJULgVrRnytB9Gji6IEhEzlK6q4eTLvx45TAJdXVd7Lnn2q

　　4.如果P（w1）=0.8， P（w2 ）=P（w3 ）=0.1，再進行第二步和第三步實驗。實驗的結果如下：

　　首先是得出三類樣本點各自的均值和協方差矩陣：

　　

　　

　　在三個類別的先驗概率均為P（w1）=P（w2 ）=P（w3 ）=1/3時，使用函數進行分類并給出分類結果和各個測試點與各個類別均值之間的Mahalanobis距離。

　　

　　

　　

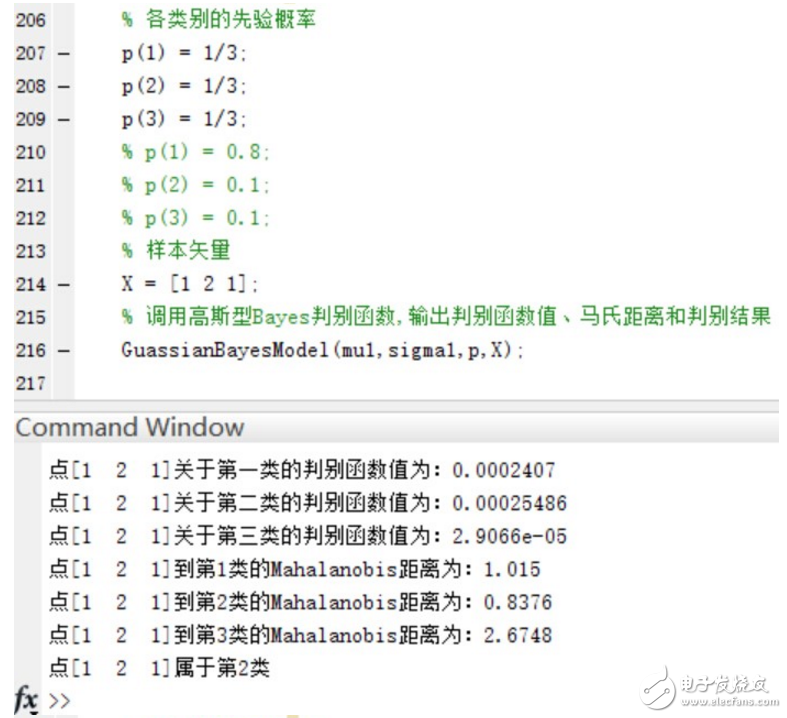
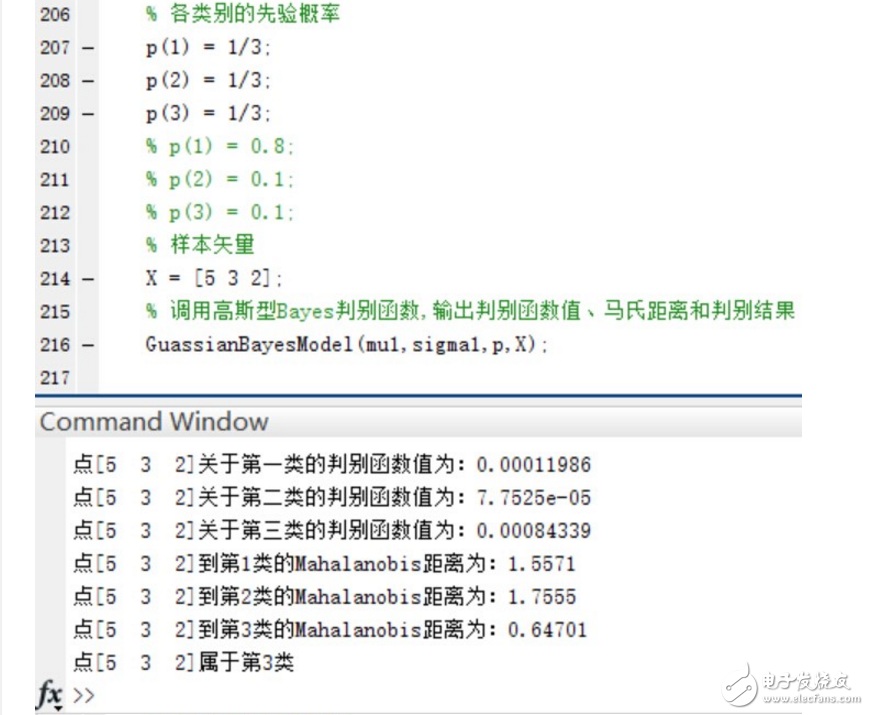
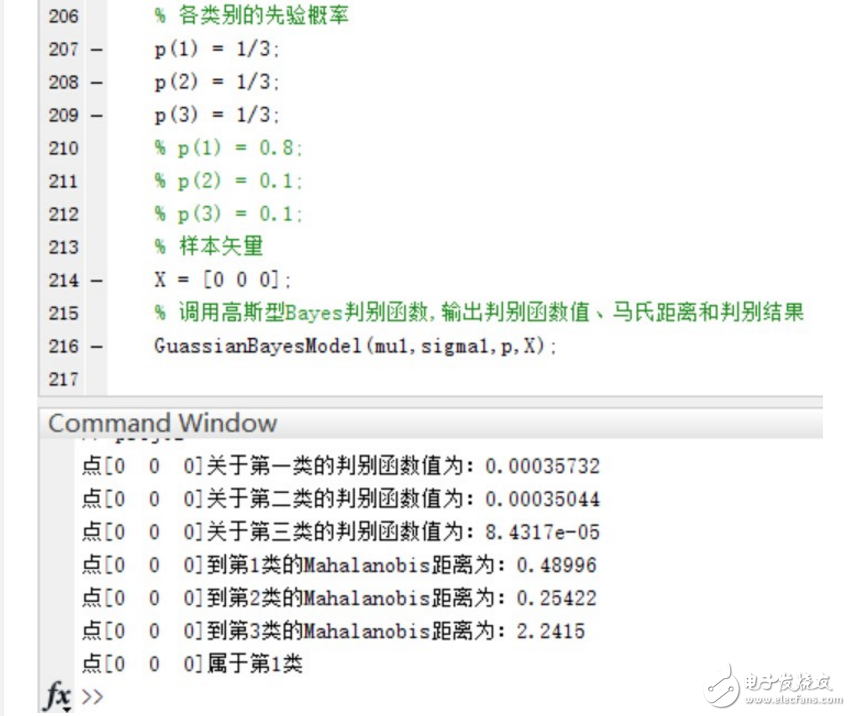
　　驗證當三個類別的先驗概率不相等時，同樣使用函數進行分類并給出分類結果和各個測試點與各個類別均值之間的Mahalanobis距離。

　　

　　

　　

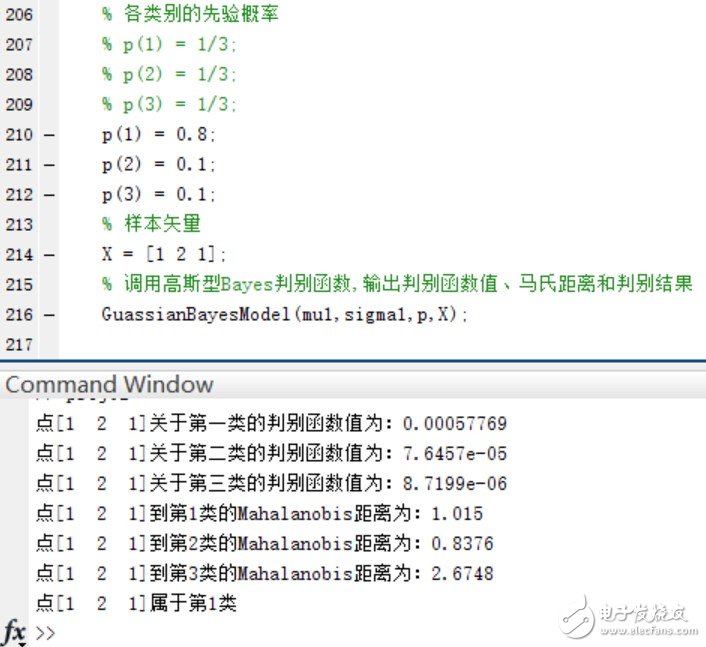
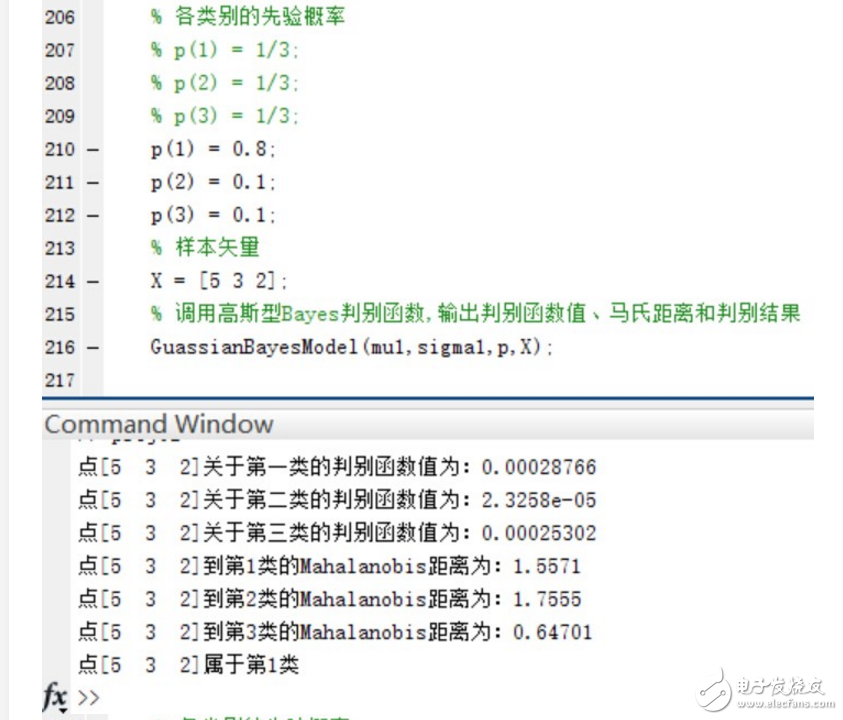
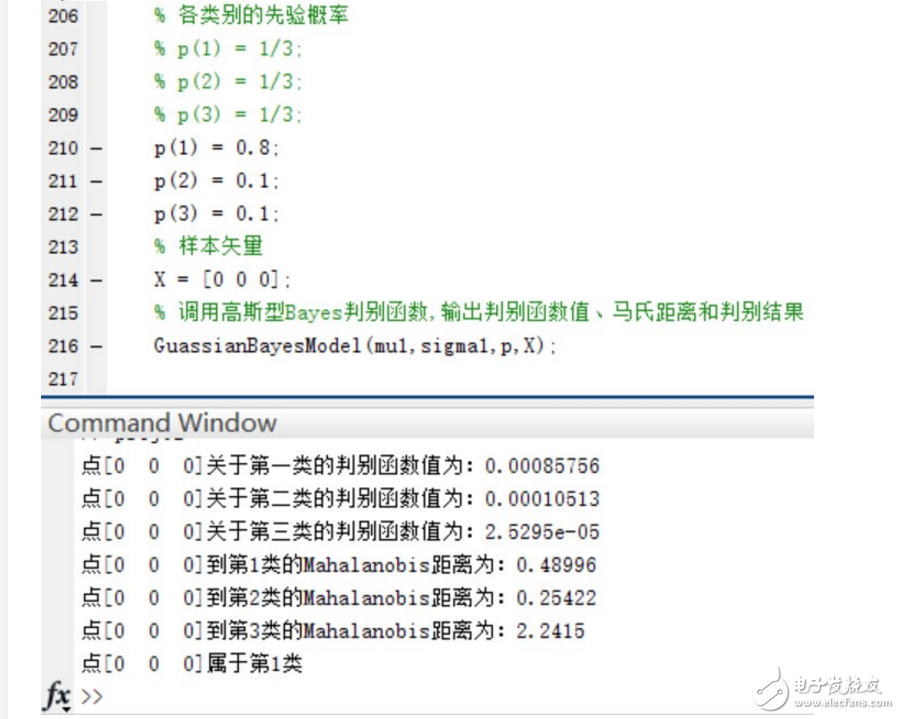
　　可以看到，在Mahalanobis距離不變的情況下，不同的先驗概率對高斯型Bayes分類器的分類結果影響很大~ 事實上，最優判決將偏向于先驗概率較大的類別。

　　完整的代碼如下由兩個函數和主要的執行流程組成：

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　% 產生模式類函數

　　% N：生成散點個數 C：類別個數 d：散點的維數

　　% mu：各類散點的均值矩陣

　　% sigma：各類散點的協方差矩陣

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　function result = MixGaussian（N， C， d， mu， sigma）

　　color = {‘r.’， ‘g.’， ‘m.’， ‘b.’， ‘k.’， ‘y.’}; % 用于存放不同類數據的顏色

　　% if nargin 《= 3 & N 《 0 & C 《 1 & d 《 1

　　% error（‘參數太少或參數錯誤’）;

　　if d == 1

　　for i = 1 ： C

　　for j = 1 ： N/C

　　r（j，i） = sqrt（sigma（1，i）） * randn（） + mu（1，i）;

　　end

　　X = round（mu（1，i）-5）;

　　Y = round（mu（1，i） + sqrt（sigma（1，i））+5）;

　　b = hist（r（：，i）， X:Y）;

　　subplot（1，C，i），bar（X:Y， b，‘b’）;

　　title（‘三類一維隨機點的分布直方圖’）;

　　grid on

　　end

　　elseif d == 2

　　for i = 1:C

　　r（：，：，i） = mvnrnd（mu（：，：，i），sigma（：，：，i），round（N/C））;

　　plot（r（：，1，i），r（：，2，i），char（color（i）））;

　　hold on;

　　end

　　elseif d == 3

　　for i = 1:C

　　r（：，：，i） = mvnrnd（mu（：，：，i），sigma（：，：，i），round（N/C））;

　　plot3（r（：，1，i），r（：，2，i），r（：，3，i），char（color（i）））;

　　hold on;

　　end

　　else disp（‘維數只能設置為1，2或3’）;

　　end

　　result = r;

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　% 高斯型Bayes判別函數

　　% mu：輸入正態分布的均值

　　% sigma：輸入正態分布的協方差矩陣

　　% p：輸入各類的先驗概率

　　% X：輸入樣本矢量

　　% 輸出判別函數值、馬氏距離和判別結果

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　function GuassianBayesModel（ mu，sigma，p，X ）

　　% 構建判別函數

　　% 計算點到每個類的Mahalanobis距離

　　for i = 1:3;

　　P（i） = mvnpdf（X， mu（：，：，i）， sigma（：，：，i）） * p（i）;

　　r（i） = sqrt（（X - mu（：，：，i）） * inv（sigma（：，：，i）） * （X - mu（：，：，i））‘）;

　　end

　　% 判斷樣本屬于哪個類的概率最高

　　% 并顯示點到每個類的Mahalanobis距離

　　maxP = max（P）;

　　style = find（P == maxP）;

　　disp（［’點［‘，num2str（X），’］關于第一類的判別函數值為：‘，num2str（P（1））］）;

　　disp（［’點［‘，num2str（X），’］關于第二類的判別函數值為：‘，num2str（P（2））］）;

　　disp（［’點［‘，num2str（X），’］關于第三類的判別函數值為：‘，num2str（P（3））］）;

　　disp（［’點［‘，num2str（X），’］到第1類的Mahalanobis距離為：‘，num2str（r（1））］）;

　　disp（［’點［‘，num2str（X），’］到第2類的Mahalanobis距離為：‘，num2str（r（2））］）;

　　disp（［’點［‘，num2str（X），’］到第3類的Mahalanobis距離為：‘，num2str（r（3））］）;

　　disp（［’點［‘，num2str（X），’］屬于第‘，num2str（style），’類‘］）;

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　%貝葉斯分類器實驗主函數

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　% 生成兩類各100個散點樣本

　　mu（：，：，1） = ［1 3］;

　　sigma（：，：，1） = ［1.5 0; 0 1］;

　　p1 = 1/2;

　　mu（：，：，2） = ［3 1］;

　　sigma（：，：，2） = ［1 0.5; 0.5 2］;

　　p2 = 1/2;

　　% 生成200個二維散點，平分為兩類，每類100個

　　aa = MixGaussian（200， 2， 2， mu， sigma）;

　　title（’兩類共200個高斯分布的散點‘）;

　　% 只x分量作為分類特征的分類情況

　　figure;

　　% 正確分類的散點個數

　　right1 = 0;

　　right2 = 0;

　　% 正確率

　　rightRate1 = 0;

　　rightRate2 = 0;

　　for i = 1:100

　　x = aa（i，1，1）;

　　plot（aa（：，1，1），aa（：，2，1），’r.‘）;

　　% 計算后驗概率

　　P1 = normpdf（x， 1， sqrt（1.5））;

　　P2 = normpdf（x， 3， sqrt（1））;

　　if P1 》 P2

　　plot（aa（i，1，1），aa（i，2，1），’ks‘）;

　　hold on;

　　right1 = right1 + 1;% 統計正確個數

　　elseif P1 《 P2

　　plot（aa（i，1，1），aa（i，2，1），’go‘）;

　　hold on;

　　end

　　end

　　rightRate1 = right1 / 100; % 正確率

　　for i = 1:100

　　x = aa（i，1，2）;

　　plot（aa（：，1，2），aa（：，2，2），’g.‘）;

　　% 計算后驗概率

　　P1 = normpdf（x， 1， sqrt（1.5））;

　　P2 = normpdf（x， 3， sqrt（1））;

　　if P1 》 P2

　　plot（aa（i，1，2），aa（i，2，2），’ks‘）;

　　hold on;

　　elseif P1 《 P2

　　plot（aa（i，1，2），aa（i，2，2），’go‘）;

　　hold on;

　　right2 = right2 + 1; % 統計正確個數

　　end

　　end

　　rightRate2 = right2 / 100;

　　title（’使用第一個分類特征的分類結果‘）;

　　disp（［’只用第一個特征時，第一類分類的準確率為：‘，num2str（rightRate1*100），’%‘］）;

　　disp（［’只用第一個特征時，第二類分類的準確率為：‘，num2str（rightRate2*100），’%‘］）;

　　% 只使用y分量的分類特征的分類情況

　　figure;

　　% 正確分類的散點個數

　　right1 = 0;

　　right2 = 0;

　　% 正確率

　　rightRate1 = 0;

　　rightRate2 = 0;

　　for i = 1:100

　　y = aa（i，2，1）;

　　plot（aa（：，1，1），aa（：，2，1），’r.‘）;

　　% 計算后驗概率

　　P1 = normpdf（y， 3， sqrt（1））;

　　P2 = normpdf（y， 1， sqrt（2））;

　　if P1 》 P2

　　plot（aa（i，1，1），aa（i，2，1），’ks‘）;

　　hold on;

　　right1 = right1 + 1; % 統計正確個數

　　elseif P1 《 P2

　　plot（aa（i，1，1），aa（i，2，1），’go‘）;

　　hold on;

　　end

　　end

　　rightRate1 = right1 / 100; % 正確率

　　for i = 1:100

　　y = aa（i，2，2）;

　　plot（aa（：，1，2），aa（：，2，2），’g.‘）;

　　% 計算后驗概率

　　P1 = normpdf（y， 3， sqrt（1））;

　　P2 = normpdf（y， 1， sqrt（2））;

　　if P1 》 P2

　　plot（aa（i，1，2），aa（i，2，2），’ks‘）;

　　hold on;

　　elseif P1 《 P2

　　plot（aa（i，1，2），aa（i，2，2），’go‘）;

　　hold on;

　　right2 = right2 + 1; % 統計正確個數

　　end

　　end

　　rightRate2 = right2 / 100; % 正確率

　　title（’使用第二個分類特征的分類結果‘）;

　　disp（［’只用第二個特征時，第一類分類的準確率為：‘，num2str（rightRate1*100），’%‘］）;

　　disp（［’只用第二個特征時，第二類分類的準確率為：‘，num2str（rightRate2*100），’%‘］）;

　　% 同時使用兩個分類特征的分類情況

　　figure;

　　% 正確分類的散點個數

　　right1 = 0;

　　right2 = 0;

　　% 正確率

　　rightRate1 = 0;

　　rightRate2 = 0;

　　for i = 1:100

　　x = aa（i，1，1）;

　　y = aa（i，2，1）;

　　plot（aa（：，1，1），aa（：，2，1），’r.‘）;

　　% 計算后驗概率

　　P1 = mvnpdf（［x，y］， mu（：，：，1）， sigma（：，：，1））;

　　P2 = mvnpdf（［x，y］， mu（：，：，2）， sigma（：，：，2））;

　　if P1 》 P2

　　plot（aa（i，1，1），aa（i，2，1），’ks‘）;

　　hold on;

　　right1 = right1 + 1;

　　else if P1 《 P2

　　plot（aa（i，1，1），aa（i，2，1），’go‘）;

　　hold on;

　　end

　　end

　　end

　　rightRate1 = right1 / 100;

　　for i = 1:100

　　x = aa（i，1，2）;

　　y = aa（i，2，2）;

　　plot（aa（：，1，2），aa（：，2，2），’g.‘）;

　　% 計算后驗概率

　　P1 = mvnpdf（［x，y］， mu（：，：，1）， sigma（：，：，1））;

　　P2 = mvnpdf（［x，y］， mu（：，：，2）， sigma（：，：，2））;

　　if P1 》 P2

　　plot（aa（i，1，2），aa（i，2，2），’ks‘）;

　　hold on;

　　else if P1 《 P2

　　plot（aa（i，1，2），aa（i，2，2），’go‘）;

　　hold on;

　　right2 = right2 + 1;

　　end

　　end

　　end

　　rightRate2 = right2 / 100;

　　title（’使用兩個分類特征的分類結果‘）;

　　disp（［’同時使用兩個特征時，第一類分類的準確率為：‘，num2str（rightRate1*100），’%‘］）;

　　disp（［’同時使用兩個特征時，第二類分類的準確率為：‘，num2str（rightRate2*100），’%‘］）;

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　% 進一步的Bayes分類器

　　%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

　　% w1，w2，w3三類散點

　　w = zeros（10，3，3）;

　　w（：，：，1） = ［-5.01 -8.12 -3.68;。。。

　　-5.43 -3.48 -3.54;。。。

　　1.08 -5.52 1.66;。。。

　　0.86 -3.78 -4.11;。。。

　　-2.67 0.63 7.39;。。。

　　4.94 3.29 2.08;。。。

　　-2.51 2.09 -2.59;。。。

　　-2.25 -2.13 -6.94;。。。

　　5.56 2.86 -2.26;。。。

　　1.03 -3.33 4.33］;

　　w（：，：，2） = ［-0.91 -0.18 -0.05;。。。

　　1.30 -.206 -3.53;。。。

　　-7.75 -4.54 -0.95;。。。

　　-5.47 0.50 3.92;。。。

　　6.14 5.72 -4.85;。。。

　　3.60 1.26 4.36;。。。

　　5.37 -4.63 -3.65;。。。

　　7.18 1.46 -6.66;。。。

　　-7.39 1.17 6.30;。。。

　　-7.50 -6.32 -0.31］;

　　w（：，：，3） = ［ 5.35 2.26 8.13;。。。

　　5.12 3.22 -2.66;。。。

　　-1.34 -5.31 -9.87;。。。

　　4.48 3.42 5.19;。。。

　　7.11 2.39 9.21;。。。

　　7.17 4.33 -0.98;。。。

　　5.75 3.97 6.65;。。。

　　0.77 0.27 2.41;。。。

　　0.90 -0.43 -8.71;。。。

　　3.52 -0.36 6.43］;

　　% 均值

　　mu1（：，：，1） = sum（w（：，：，1）） 。/ 10;

　　mu1（：，：，2） = sum（w（：，：，2）） 。/ 10;

　　mu1（：，：，3） = sum（w（：，：，3）） 。/ 10;

　　% 協方差矩陣

　　sigma1（：，：，1） = cov（w（：，：，1））;

　　sigma1（：，：，2） = cov（w（：，：，2））;

　　sigma1（：，：，3） = cov（w（：，：，3））;

　　% 各類別的先驗概率

　　% p（1） = 1/3;

　　% p（2） = 1/3;

　　% p（3） = 1/3;

　　p（1） = 0.8;

　　p（2） = 0.1;

　　p（3） = 0.1;

　　% 樣本矢量

　　X = ［1 0 0］;

　　% 調用高斯型Bayes判別函數，輸出判別函數值、馬氏距離和判別結果

　　GuassianBayesModel（mu1，sigma1，p，X）;