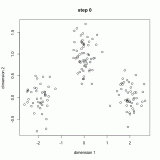
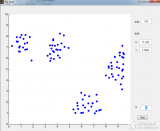
左圖是K取值從2到7時(shí)的聚類效果,右圖是K取值從2到9時(shí)的類簇指標(biāo)的變化曲線,此處我選擇類簇指標(biāo)是K個(gè)類簇的平均質(zhì)心距離的加權(quán)平均值。從上圖中可以明顯看到,當(dāng)K取值5時(shí),類簇指標(biāo)的下降趨勢最快,所以K的正確取值應(yīng)該是5.為以下是具體數(shù)據(jù):
《span style=“background-color: white;”》2 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 8.51916676443
所有類簇的平均質(zhì)心距離的加權(quán)平均值 4.82716260322
3 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 7.58444829472
所有類簇的平均質(zhì)心距離的加權(quán)平均值 3.37661824845
4 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 5.65489660064
所有類簇的平均質(zhì)心距離的加權(quán)平均值 2.22135360453
5 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 3.67478798553
所有類簇的平均質(zhì)心距離的加權(quán)平均值 1.25657641195
6 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 3.44686996398
所有類簇的平均質(zhì)心距離的加權(quán)平均值 1.20944264145
7 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 3.3036641135
所有類簇的平均質(zhì)心距離的加權(quán)平均值 1.16653919186
8 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 3.30268530308
所有類簇的平均質(zhì)心距離的加權(quán)平均值 1.11361639906
9 個(gè)聚類
所有類簇的半徑的加權(quán)平均值 3.17924400582
所有類簇的平均質(zhì)心距離的加權(quán)平均值 1.07431888569《/span》
uk是第k 個(gè)類的重心位置。成本函數(shù)是各個(gè)類畸變程度(distortions)之和。每個(gè)類的畸變程度等于該類重心與其內(nèi)部成員位置距離的平方和。若類內(nèi)部的成員彼此間越緊湊則類的畸變程度越小,反之,若類內(nèi)部的成員彼此間越分散則類的畸變程度越大。求解成本函數(shù)最小化的參數(shù)就是一個(gè)重復(fù)配置每個(gè)類包含的觀測值,并不斷移動(dòng)類重心的過程。
#-*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import sys
reload(sys)
sys.setdefaultencoding(‘utf-8’)
x = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
y = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
data = np.array(list(zip(x, y)))
# 肘部法則 求解最佳分類數(shù)
# K-Means參數(shù)的最優(yōu)解也是以成本函數(shù)最小化為目標(biāo)
# 成本函數(shù)是各個(gè)類畸變程度(distortions)之和。每個(gè)類的畸變程度等于該類重心與其內(nèi)部成員位置距離的平方和
‘’‘’‘a(chǎn)a=[]
K = range(1, 10)
for k in range(1,10):
kmeans=KMeans(n_clusters=k)
kmeans.fit(data)
aa.append(sum(np.min(cdist(data, kmeans.cluster_centers_, ’euclidean‘),axis=1))/data.shape[0])
plt.figure()
plt.plot(np.array(K), aa, ’bx-‘)
plt.show()’‘’
#繪制散點(diǎn)圖及聚類結(jié)果中心點(diǎn)
plt.figure()
plt.axis([0, 10, 0, 10])
plt.grid(True)
plt.plot(x,y,‘k.’)
kmeans=KMeans(n_clusters=3)
kmeans.fit(data)
plt.plot(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],‘r.’)
plt.show()
 電子發(fā)燒友App
電子發(fā)燒友App









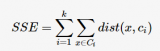


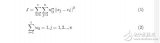










評(píng)論