聚類分析是多元統計分析的一種,也是無監督模式識別的一個重要分支,在模式分類 圖像處理和模糊規則處理等眾多領域中獲得最廣泛的應用。它把一個沒有類別標記的樣本按照某種準則劃分為若干子集,使相似的樣本盡可能歸于一類,而把不相似的樣本劃分到不同的類中。硬聚類把每個待識別的對象嚴格的劃分某類中,具有非此即彼的性質,而模糊聚類建立了樣本對類別的不確定描述,更能客觀的反應客觀世界,從而成為聚類分析的主流。
模糊聚類算法是一種基于函數最優方法的聚類算法,使用微積分計算技術求最優代價函數,在基于概率算法的聚類方法中將使用概率密度函數,為此要假定合適的模型,模糊聚類算法的向量可以同時屬于多個聚類,從而擺脫上述問題。
模糊聚類分析算法大致可分為三類
1)分類數不定,根據不同要求對事物進行動態聚類,此類方法是基于模糊等價矩陣聚類的,稱為模糊等價矩陣動態聚類分析法。
2)分類數給定,尋找出對事物的最佳分析方案,此類方法是基于目標函數聚類的,稱為模糊C均值聚類。
3)在攝動有意義的情況下,根據模糊相似矩陣聚類,此類方法稱為基于攝動的模糊聚類分析法
模糊的c均值聚類算法:-------- 一種模糊聚類算法,是k均值聚類算法的推廣形式,隸屬度取值為[0 1]區間內的任何一個數,提出的基本根據是“類內加權誤差平方和最小化”準則;
模糊C 均值聚類算法(FCM,Fuzzy c-means) 是從硬C 均值聚類算法發展而來(HCM,Hardc-means )。
硬C劃分和模糊C 劃分

FCM算法原理

FCM 算法步驟
給定聚類類別數C,設定迭代收斂條件,初始化各個聚類中心;
(1)重復下面的運算,直到各個樣本的隸屬度值穩定:
(2)用當前的聚類中心根據公式(6) 計算隸屬度函數;
A.用當前的隸屬度函數根據公式(5) 重新計算各個聚類的中心。
B.當算法收斂時,就得到了各類的聚類中心和各個樣本對于各類的隸屬度值,從而完成了模糊聚類劃分。
算法實現
·采用VC++進行編寫
文檔的讀取
#include “data.h”
//函數定義
double **DataRead(char*name,int row,intcol)
{
double**p=new double* [row];
ifstreaminfile;
infile.open(name,ios::in);
for(inti=0;i《row;i++)
{
p[i]=newdouble[col];
for(intj=0;j《col;j++)
{
infile》》p[i][j];
}
}
infile.close();
cout《《“成功讀取數據文件:”《《name《《“!\n”;
returnp;
//釋放內存
for(i=0;i《row;i++)
{
delete[]p[i];
}
delete[]p;
}
文檔的保存
#include “data.h”
void DataSave(double**data,int row,intcol,char*name)
{
inti,j;
ofstreamoutfile;
//打開文件,輸出數據
outfile.open(name,ios::out);
outfile.setf(ios::fixed);
outfile.precision(4);
for(i=0;i《row;i++)
{
for(j=0;j《col;j++)
{
outfile《《data[i][j]《《“”;
}
outfile《《endl;
}
outfile《《endl《《endl;
outfile.close();
}
數據標準化處理
#include “data.h”
double **Standardize(double **data,introw,int col)
{
inti,j;
double*a=new double[col]; //矩陣每列的最大值
double*b=new double[col]; //矩陣每列的最小值
double*c=new double[row]; //矩陣列元素
for(i=0;i《col;i++)
{
//取出數據矩陣的各列元素
for(j=0;j《row;j++)
{
c[j]=Data[j][i];
}
a[i]=c[0],b[i]=c[0];
for(j=0;j《row;j++)
{
//取出該列的最大值
if(c[j]》a[i])
{
a[i]=c[j];
}
//取出該列的最小值
if(c[j]《b[i])
{
b[i]=c[j];
}
}
}
//數據標準化
for(i=0;i《row;i++)
{
for(j=0;j《col;j++)
{
data[i][j]=(data[i][j]-b[j])/(a[j]-b[j]);
}
}
cout《《“完成數據極差標準化處理!\n”;
delete[]a;
delete[]b;
delete[]c;
returndata;
}
生成樣本慮屬矩陣
#include “data.h”
void Initialize(double **u, int k, introw)
{
inti,j;
//初始化樣本隸屬度矩陣
srand(time(0));
for(i=0;i《k;i++)
{
for(j=0;j《row;j++)
{
u[i][j]=(double)rand()/RAND_MAX;//得到一個小于1的小數隸屬度
}//rand()函數返回0和RAND_MAX之間的一個偽隨機數
}
}
數據歸一化處理
#include “data.h”
void Normalize(double **u,int k,intcol)
{
inti,j;
double*sum=new double[col];
//矩陣U的各列元素之和
for(j=0;j《col;j++)
{
doubledj=0;
for(i=0;i《k;i++)
{
dj=dj+U[i][j];
sum[j]=dj;//隸屬度各列之和
}
}
for(i=0;i《k;i++)
{
for(j=0;j《col;j++)
{
u[i][j]=U[i][j]/sum[j];
}//規一化處理(每列隸屬度之和為1)
}
}
迭代過程
#include “data.h”
#include “func.h”//對模糊C均值進行迭代運算,并返回有效性評價函數的值
doubleUpdate(double**u,double**data,double**center,int row,int col, int k)
{
inti,j,t;
double**p=NULL;
for(i=0;i《k;i++)
{
for(j=0;j《row;j++)
{
//模糊指數取2
u[i][j]=pow(u[i][j],2);
}
}
//根據隸屬度矩陣計算聚類中心
p=MatrixMul(u,k,row,data,row,col);
for(i=0;i《k;i++)
{
//計算隸屬度矩陣每行之和
doublesi=0;
for(j=0;j《row;j++)
{
si+=u[i][j];
}
for(t=0;t《col;t++)
{
center[i][t]=p[i][t]/si; //類中心
}
}
//計算各個聚類中心i分別到所有點j的距離矩陣dis(i,j)
double*a=new double[col]; //第一個樣本點
double*b=new double[col]; //第二個樣本點
double**dis=newdouble*[k]; //中心與樣本之間距離矩陣
for(i=0;i《k;i++)
{
dis[i]=newdouble[row];
}
for(i=0;i《k; i++)
{
//聚類中心
for(t=0;t《col; t++)
{
a[t]=center[i][t]; //暫存類中心
}
//數據樣本
for(j=0;j《row; j++)
{
for(t=0;t《col; t++)
{
b[t]=data[j][t];//暫存一樣本
}
doubled=0;
//中心與樣本之間距離的計算
for(t=0;t《col; t++)
{
d+=(a[t]-b[t])*(a[t]-b[t]); //d為一中心與所有樣本的距離的平方和
}
dis[i][j]=sqrt(d); //距離
}
}
//根據距離矩陣計算隸屬度矩陣
for(i=0;i《k;i++)
{
for(j=0;j《row;j++)
{
doubletemp=0;
for(t=0;t《k;t++)
{
//dis[i][j]依次除以所在列的各元素,加和;
//模糊指數為2.0
temp+=pow(dis[i][j]/dis[t][j],2/(2.0-1));//一個類中心和一個元素的距離平方與
}
u[i][j]=1/temp;//所有類與該元素距離平方的和的商
}
}
//計算聚類有效性評價函數
doublefunc1=0;
for(i=0;i《k;i++)
{
doublefunc2=0;
for(j=0;j《row;j++)
{
func2+=pow(u[i][j],2.0)*pow(dis[i][j],2);
}
func1+=func2;
}
doubleobj_fcn=1/(1+func1);
returnobj_fcn;
//內存釋放
delete[]a;
delete[]b;
for(i=0;i《k;i++)
{
delete[]dis[i];
}
delete[]dis;
}
詳細過程
#include “data.h”
#include “func.h”
#include “max.h”
//全局變量定義
double **Data; //數據矩陣
double **Center; //聚類中心矩陣
double **U; //樣本隸屬度矩陣
int m; //樣本總數
int n; //樣本屬性數
int k; //設定的劃分類別數
int main()
{
intLab; //數據文件標號
intnum; //算法運行次數
///////////////////////////////////////////////////////////////
cout《《“模糊C均值聚類算法:”《《endl;
cout《《“1-iris.txt; 2-wine.txt; 3-ASD_12_2.txt; 4-ASD_14_2.txt”《《endl;
cout《《“請選擇數據集: Lab=”;
cin》》Lab;
cout《《“設定運行次數: mum=”;
cin》》num;
//各次運行結束后的目標函數
double*Index=new double[num];
//各次運行結束后的聚類正確率
double*R=new double [num];
//num次運行的平均目標函數及平均正確率
doubleM_Index=0;
doubleM_R=0;
//FCM聚類算法運行num次,并保存記錄與結果
for(inti=0;i《num;i++)
{
intj;
doubleepsilon=1e-4;
inte=0;
intnx=0;
//記錄連續無改進次數
intE[200]={0};
if(i》0)
{
cout《《endl《《endl;
cout《《setfill(‘#’)《《setw(10)《《endl;
}
cout《《“第”《《i+1《《“次運行記錄:”《《endl;
//讀取數據文件
if(Lab==1)
{
m=150;
n=4;
k=3;
Data=DataRead(“dataset\\iris.txt”,m,n);
}
elseif(Lab==2)
{
m=178;
n=13;
k=3;
Data=DataRead(“dataset\\wine.txt”,m,n);
}
elseif(Lab==3)
{
m=535;
n=2;
k=12;
Data=DataRead(“dataset\\ASD_12_2.txt”,m,n);
}
elseif(Lab==4)
{
m=685;
n=2;
k=14;
Data=DataRead(“dataset\\ASD_14_2.txt”,m,n);
}
//數據極差標準化處理
Data=Standardize(Data,m,n);
//聚類中心及隸屬度矩陣,內存分配
Center=newdouble*[k];
U=newdouble *[k];
for(j=0;j《k;j++)
{
Center[j]=newdouble[n];
U[j]=newdouble[m];
}
//隸屬度矩陣的初始化
Initialize(U,k, m);
//對隸屬度矩陣進行歸一化
Normalize(U,k,m);
//歷次迭代過程中的目標函數
doubleObjfcn[100]={0};
cout《《“第”《《i+1《《“次運行記錄:”《《endl;
cout《《“開始迭代過程!”《《endl;
cout《《“*******************************”《《endl;
//輸出精度為小數點后5位
cout.precision(5);
//固定格式
cout.setf(ios::fixed);
//目標函數連續20代無改進,停止該次聚類迭代過程
while(e《20)
{
nx++;
//聚類迭代過程
Objfcn[nx]=Update(U,Data,Center,m,n,k);
//統計目標函數連續無改進次數e
if(nx》0&& Objfcn[nx]-Objfcn[nx-1]《epsilon )
{
e++;
}
else
{
e=0;
}
E[nx]=e;
}
//輸出結果到文件,保存
ofstreamoutfile(“運行記錄.txt”,ios::app);
outfile《《“第”《《i+1《《“次運行記錄:”《《endl;
outfile《《“開始迭代過程!”《《endl;
outfile《《“*******************************”《《endl;
outfile.precision(5);
outfile.setf(ios::fixed);
for(intn1=1;n1《=nx;n1++)
{
cout《《“e[”《《setw(2)《《n1《《“]=”《《setw(2)《《E[n1]《《“ Objfcn[”
《《setw(2)《《n1《《“]=”《《Objfcn[n1]《《“\n”;
//保存數據文件
outfile《《“e[”《《setw(2)《《n1《《“]=”《《setw(2)《《E[n1]《《“ Objfcn[”
《《setw(2)《《n1《《“]=”《《Objfcn[n1]《《“\n”;
}
cout《《endl;
outfile《《endl;
outfile.close();
//本次運行的最大目標函數
Index[i]=Objfcn[nx];
//保存聚類正確率,輸出聚類結果:
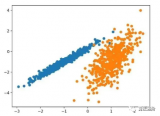
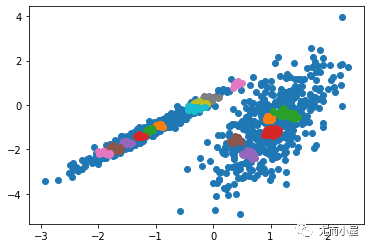
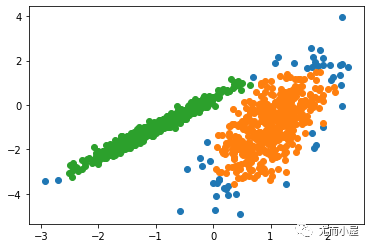
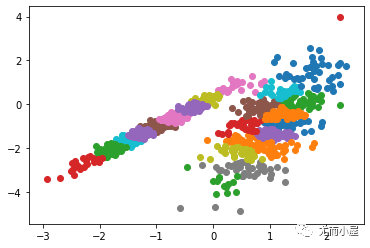
R[i]=Result(Lab,U, k, m, i);
//內存釋放
for(j=0;j《k;j++)
{
delete[]Center[j];
delete[]U[j];
}
delete[]Center;
delete[]U;
}
//////////////////////////統計平均///////////////////////////////////
doubletemp1=0, temp2=0;
for(i=0;i《num;i++)
{
temp1+=Index[i];
temp2+=R[i];
}
//計算各次結果的統計平均
M_Index=(double)temp1/num;
M_R=(double)temp2/num;
cout《《“//////////////////////////////////////////////////////////////”《《endl;
cout《《num《《“次運行,平均聚類正確率: ”《《100*M_R《《“%”《《endl;
//輸出精度為小數點后6位
cout.precision(6);
//固定格式
cout.setf(ios::fixed);
cout《《“平均目標函數:”《《M_Index《《endl;
//統計結果文件保存
ofstreamresultfile(“聚類結果.txt”,ios::app);
resultfile《《“//////////////////////////////////////////////////////////////”《《endl;
resultfile《《num《《“次運行,平均聚類正確率: ”《《100*M_R《《“%”《《endl;
//輸出精度為小數點后6位
resultfile.precision(6);
//固定格式
resultfile.setf(ios::fixed);
resultfile《《“平均目標函數:”《《M_Index《《endl;
return0;
}
 電子發燒友App
電子發燒友App









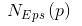










評論