疊加原理和等效電源定理

#e#

2、疊加原理和等效電源定理

疊加原理是分析線性電路時普遍適用的基本原理。使用疊加原理時，要把原電路分成幾個分電路，先求出各分電路的電壓或電流，然后求代數和得出原電路的總電壓或總電流。方法要點：首先標定原電路各支路電流、電壓的參考方向；將電路分解為各理想電源單獨作用的分電路，標出各分電路中電流（電壓）的參考方向；求解分電路中各支路電流（電壓）；最后疊加求解出原電路的電流（電壓）響應一求各分電路對應支路電流（電壓）代數和，凡分電路電流（電壓）參考方向與原電路電流（電壓）參考方向一致者取正號，反之取負號，但保留分電流本身的符號。

圖1電路用疊加原理求解，由于原電路中有兩個獨立電源，所以可把原電路用2個簡單電路疊加表示。

當電流源單獨作用時，電壓源短接。如圖3所示電路。

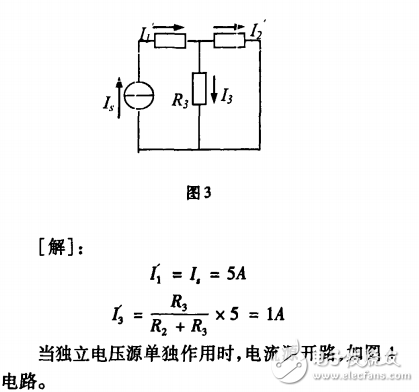
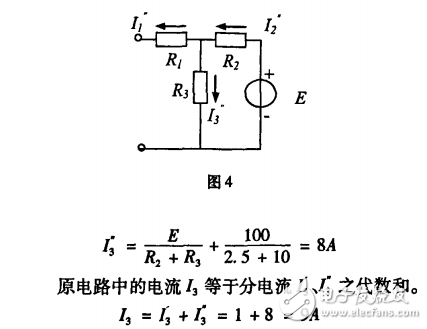
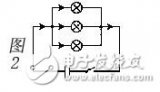
當然對圖2電路需要對3個分電路分別計算，然后再疊加。即當獨立電源較多時，這一方法就不可取了。一般疊加原理用于計算電路結構較復雜但獨立電源不多的電路。

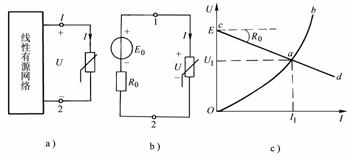
當1個復雜電路只需求解其中1條支路的電流或電壓時，那么用等效電源定理就比較方便。一般情況下，任何線性有源二端網絡可以用1個電動勢為E的理想電壓源和內阻Ro串聯的電源來等效代替，該定理就是戴維寧定理；或者等效成電流為I。的理想電流源和等效電阻Ro的并聯組合代替，即諾頓定理。

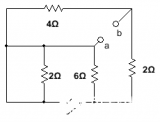
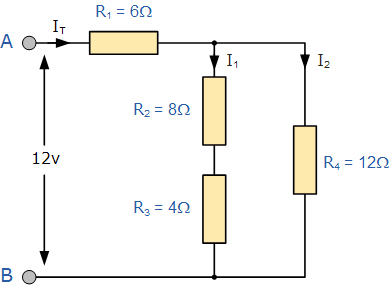
對圖2電路若只求R4支路電流。用戴維寧定理求解就比較方便。

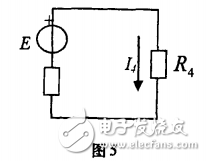
［解］：其戴維寧等效電路如圖5，其中的等效電勢E等于把毗支路開路時的端口開路電壓，如圖6所示電路；

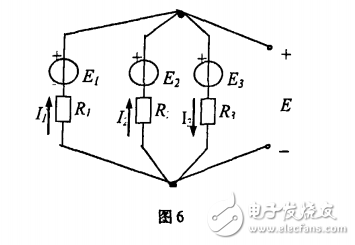
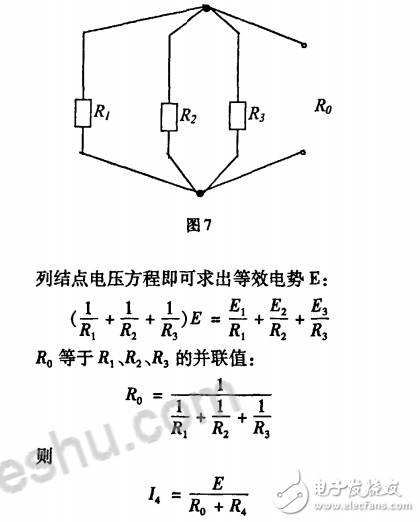
通過以上實例對比，給我們在分析電阻電路時的啟示有：電阻電路的分析和計算的最佳方法選擇應根據電路的結構和要求來確定。在支路數不多且要求解各支路電流的電路可以選擇用支路電流法；在電路結點數少，但結點間聯接的支路較多的電路可以選擇結點電壓法；在電路結構復雜但電路中獨立電源不多的電路分析求解時可以選擇疊加原理；等效電源定理是1種簡單有效的方法，往往適用于只求一部分電路的電流或電壓。