1、定義
在線性電路中,當全部激勵(獨立電壓源、電流源)同時增大K倍(縮小K倍),其響應(支路電流或電壓)也相應的增大(縮小)K倍。
齊次定理的證明
n次齊次函數定義: f(tx,ty)=t的n次冪*f(x,y) 對任意實數t都成立所以可以把等式的左右邊都看成關于x,y,t的三元函數。
假定f可以微分上式兩邊都對t求偏導數,再化簡(偏導符號假定為¢)設u=tx,v=ty 即得 (¢f/¢u)*(¢u/¢t)+(¢f/¢v)*(¢v/¢t)=n*t的n-1次冪*f(x,y) 因為f(u,v)=t的n次冪*f(x,y) 代入上式 (¢f/¢u)*x+(¢f/¢v)*y=n*f(u,v)/t 所以 (¢f/¢u)*u+(¢f/¢v)*v=n*f(u,v)
當電路中只有一個激勵(獨立源)時,則響應(電壓或電流)與激勵成正比。

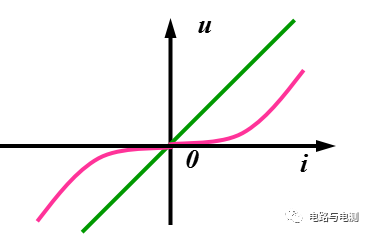
齊次定理只適用于線性電路,它描述了線性電路的比例特性。
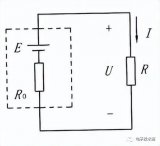
例如:
顯而易見:
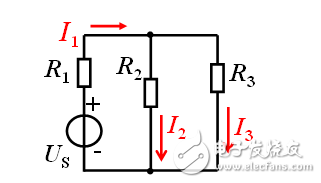
若US增加 n 倍,各電流也會增加 n 倍。
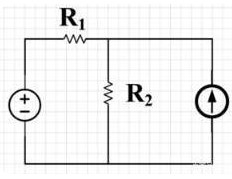
2、應用:用齊次定理分析梯形電路特別有效
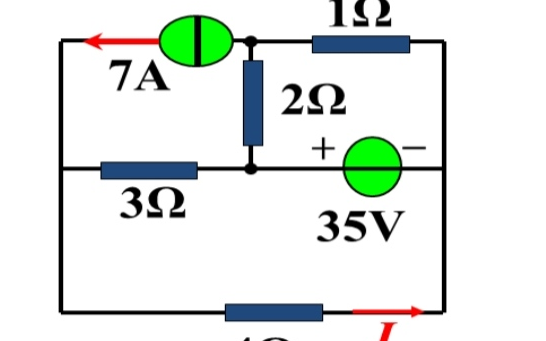
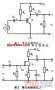
例5. 已知:RL= 2Ω,R1= 1Ω,R2= 1Ω,uS= 51V。
求電流 i 。
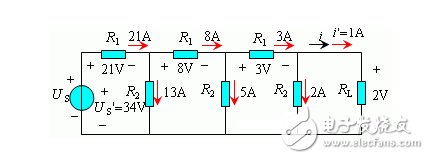
解:方法1:分壓、分流。
方法2:電源變換。
方法3:用齊性原理(單位電流法)。

本例計算是先從梯形電路最遠離電源的一段開始,倒退至激勵處。這種計算方法稱為“倒推法”。
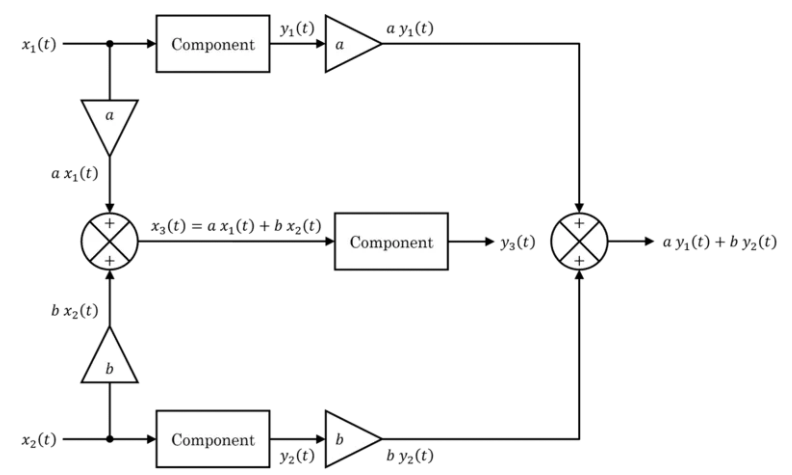
3.可加性 (additivity property)分析
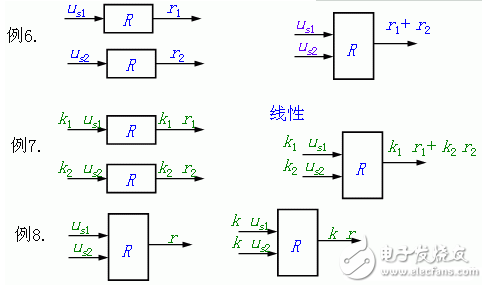
線性電路中,所有激勵都增大(或減小)同樣的倍數,則電路中響應也增大(或減小)同樣的倍數。
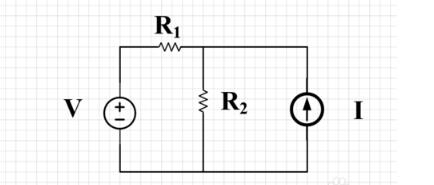
例9. 如圖電路,NS為有源網路,當US= 4V時,I3= 4A;當US= 6V時,I3= 5A;求當US= 2V時,I3為多少?
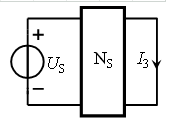
解:由疊加定理和線性定理,I3可表示為

 電子發燒友App
電子發燒友App









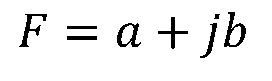





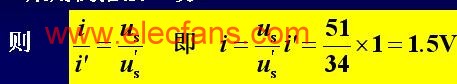
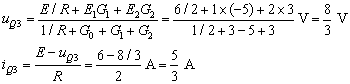











評論