今天給大家分享一下如何在資源緊張,算力較低的單片機上實現三角函數的算法。
之前發過一篇關于IQMath的文章,這個是ti公司平臺上的一個數學運算庫,里面封裝了很多高效的數學運算方法。
例如在不具備浮點運算器的定點處理器使用定點運算,以前寫過一篇Q格式的文章,有簡單介紹過這些知識。
那么問題來了,有一個讀者朋友的硬件平臺無法使用IQMath,但是他要進行一些三角函數的運算,那么該如何自己動手實現呢?
下面我們來簡單介紹一下整體的思路吧,因為硬件平臺的資源比較緊張;
所以這里比較常用的方法就是通過空間換時間,預先將sin,cos的值存儲到數組中,需要用的時候,訪問數組就可以得到具體的數據。這也就是我們經常會提到的查表法。
下面我們來詳細介紹一下。
正弦表
這個正弦函數表達式是這樣的,
?具體如下圖所示;
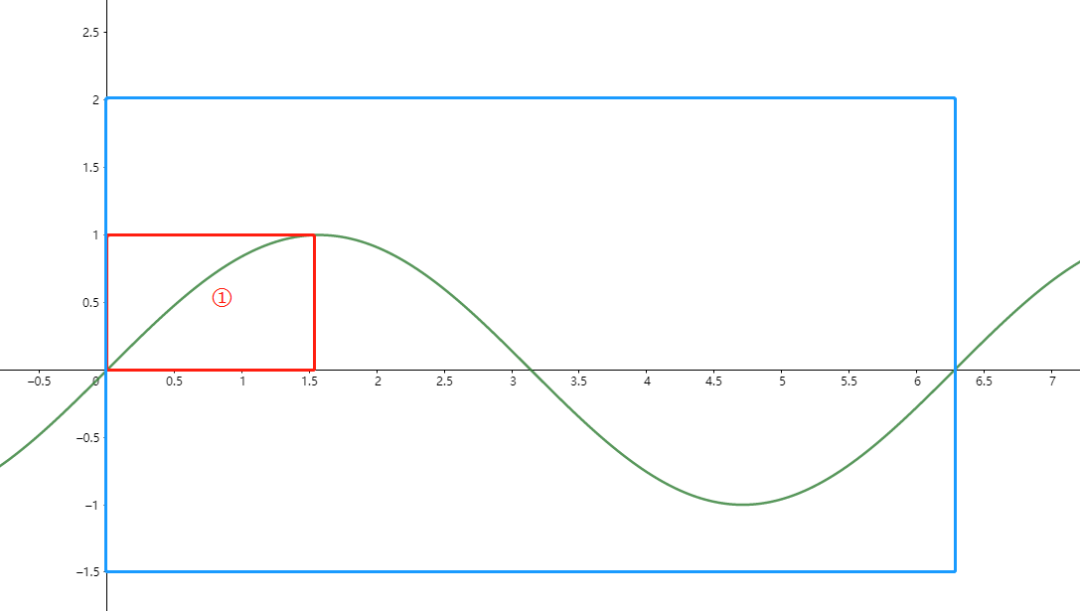 正弦波
正弦波首先我們來簡單分析一下這個波形:
- 在藍色框內是一整個周期的波形;
- 在紅色框內是四分之一個周期的波形;
其實不難發現,我們只要表示出這四分之一個波形的數據,其余剩下的波形都可以通過換算表示出來。
這樣做就大大節省了查表法所需要的空間。
下面我們來介紹一下具體如何實現;
首先我們得搞清楚一個點,就是量綱,統一用歸一化的形式來做。
-
y的范圍是
[-1, 1]; -
x的范圍是
[0, 2π],當然,x的范圍[-π, π]也是沒問題的,下面會繼續介紹;
而在實際的程序中,我們是無法這樣去做的,這些數值我們期望通過整形類型去訪問,所以我們要做到幾點:
- 盡量避免使用浮點運算;
- 盡量避免除法;
- 盡量避免乘法;
所以這里有必要先了解一下Q格式,用左移和右移去代替乘法和除法,提高運算效率;
對于X軸的數據,于是可以將[0, 2π]細分成 128 ,256,512或者 1024 等等;
這里我們先細分成1024等份,正如前面提到的,只需要選擇前四分之一周期的內容即可;
????#define?POINT_NUM??256
?#define?PI??????????3.141592f
?for?(int?i?=?0;?i?printf(?"[%03d:%1.4f] ",?i?,?(sin(i*PI/2?/?POINT_NUM)));
????????if((i+1)?%?8?==?0){
????????????printf("
");
????????}
????}
打印的輸出結果如下:
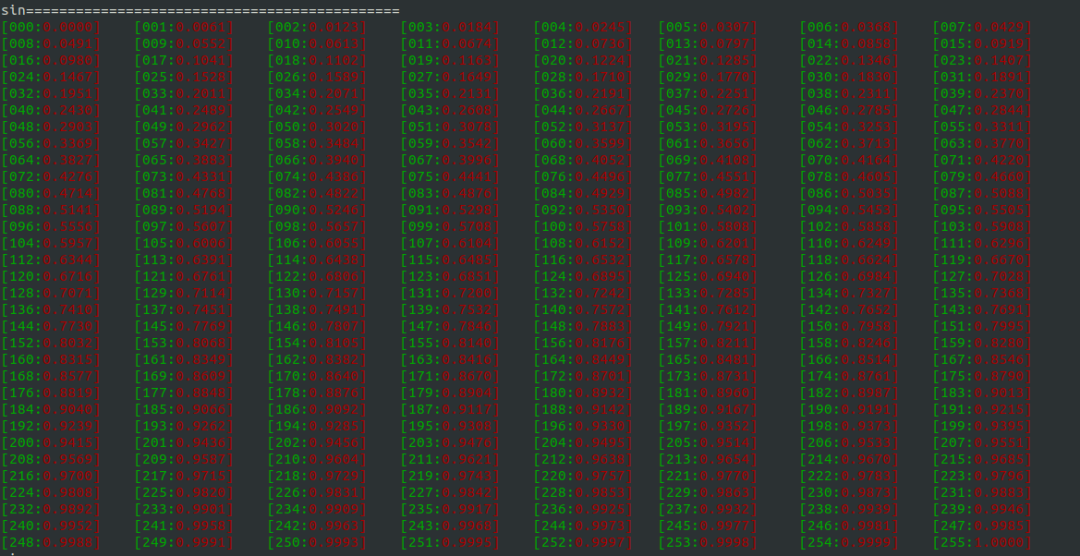 浮點類型的正弦表
浮點類型的正弦表這里我們可以簡單取幾個特殊點驗證一下,發現整體還是可以接受的;
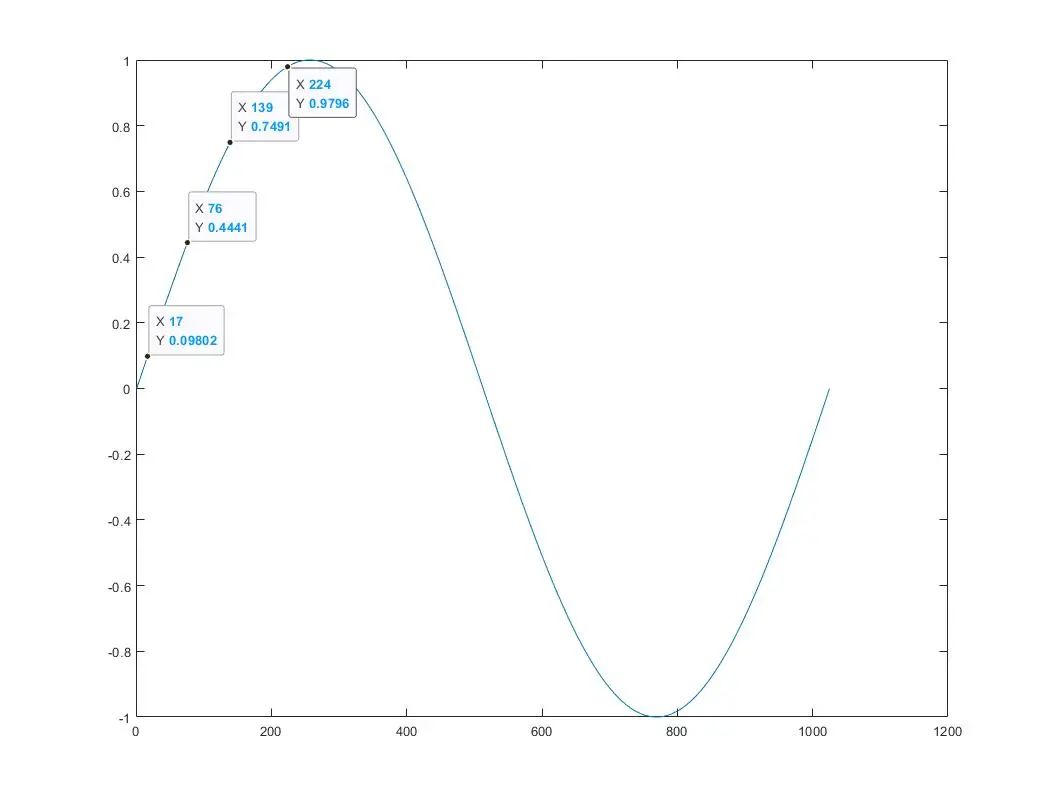 matlab輸出的波形
matlab輸出的波形
下一步就是將浮點數據y轉化為Q1.15格式哈,
#define?POINT_NUM??256
#define?PI??????????3.141592f
?printf("sin=============================================
");
????for?(int?i?=?0;?i?printf("[?%d: 0x%04X?]",?i,?(int16_t)(sin(i*PI/2?/?POINT_NUM)?*?32768));
????????if((i+1)?%?8?==?0){
????????????printf("
");
????????}
????}
最終輸出結果如下所示;
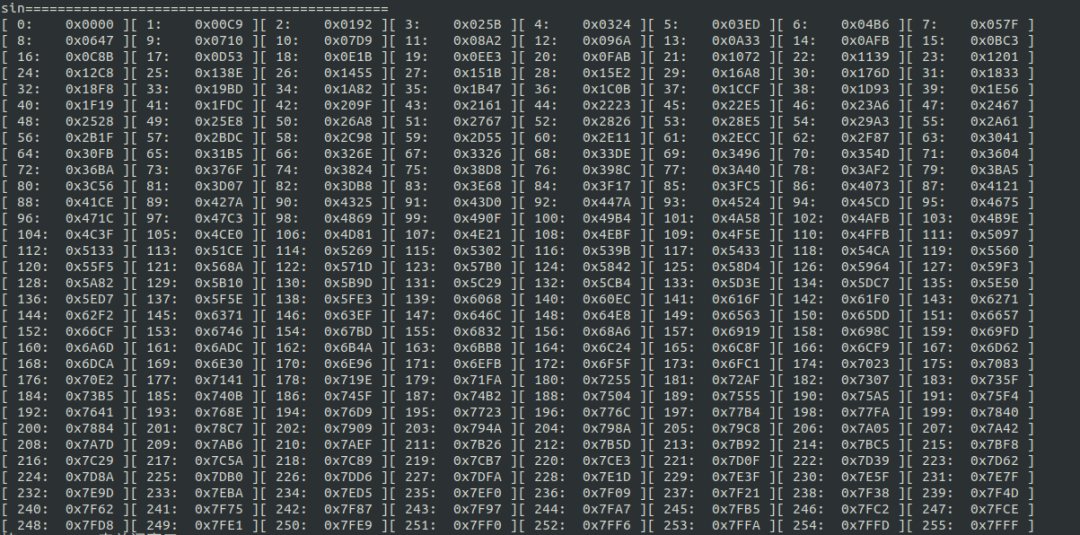 Q格式正弦表
Q格式正弦表源碼部分
下面這部分代碼是參考ST的mcsdk中的一個實例,下面我們會依次分析每個部分的作用,整體的代碼具體如下所示;
#define?SIN_COS_TABLE?{
????0x0000,0x00C9,0x0192,0x025B,0x0324,0x03ED,0x04B6,0x057F,
????0x0648,0x0711,0x07D9,0x08A2,0x096A,0x0A33,0x0AFB,0x0BC4,
????0x0C8C,0x0D54,0x0E1C,0x0EE3,0x0FAB,0x1072,0x113A,0x1201,
????0x12C8,0x138F,0x1455,0x151C,0x15E2,0x16A8,0x176E,0x1833,
????0x18F9,0x19BE,0x1A82,0x1B47,0x1C0B,0x1CCF,0x1D93,0x1E57,
????0x1F1A,0x1FDD,0x209F,0x2161,0x2223,0x22E5,0x23A6,0x2467,
????0x2528,0x25E8,0x26A8,0x2767,0x2826,0x28E5,0x29A3,0x2A61,
????0x2B1F,0x2BDC,0x2C99,0x2D55,0x2E11,0x2ECC,0x2F87,0x3041,
????0x30FB,0x31B5,0x326E,0x3326,0x33DF,0x3496,0x354D,0x3604,
????0x36BA,0x376F,0x3824,0x38D9,0x398C,0x3A40,0x3AF2,0x3BA5,
????0x3C56,0x3D07,0x3DB8,0x3E68,0x3F17,0x3FC5,0x4073,0x4121,
????0x41CE,0x427A,0x4325,0x43D0,0x447A,0x4524,0x45CD,0x4675,
????0x471C,0x47C3,0x4869,0x490F,0x49B4,0x4A58,0x4AFB,0x4B9D,
????0x4C3F,0x4CE0,0x4D81,0x4E20,0x4EBF,0x4F5D,0x4FFB,0x5097,
????0x5133,0x51CE,0x5268,0x5302,0x539B,0x5432,0x54C9,0x5560,
????0x55F5,0x568A,0x571D,0x57B0,0x5842,0x58D3,0x5964,0x59F3,
????0x5A82,0x5B0F,0x5B9C,0x5C28,0x5CB3,0x5D3E,0x5DC7,0x5E4F,
????0x5ED7,0x5F5D,0x5FE3,0x6068,0x60EB,0x616E,0x61F0,0x6271,
????0x62F1,0x6370,0x63EE,0x646C,0x64E8,0x6563,0x65DD,0x6656,
????0x66CF,0x6746,0x67BC,0x6832,0x68A6,0x6919,0x698B,0x69FD,
????0x6A6D,0x6ADC,0x6B4A,0x6BB7,0x6C23,0x6C8E,0x6CF8,0x6D61,
????0x6DC9,0x6E30,0x6E96,0x6EFB,0x6F5E,0x6FC1,0x7022,0x7083,
????0x70E2,0x7140,0x719D,0x71F9,0x7254,0x72AE,0x7307,0x735E,
????0x73B5,0x740A,0x745F,0x74B2,0x7504,0x7555,0x75A5,0x75F3,
????0x7641,0x768D,0x76D8,0x7722,0x776B,0x77B3,0x77FA,0x783F,
????0x7884,0x78C7,0x7909,0x794A,0x7989,0x79C8,0x7A05,0x7A41,
????0x7A7C,0x7AB6,0x7AEE,0x7B26,0x7B5C,0x7B91,0x7BC5,0x7BF8,
????0x7C29,0x7C59,0x7C88,0x7CB6,0x7CE3,0x7D0E,0x7D39,0x7D62,
????0x7D89,0x7DB0,0x7DD5,0x7DFA,0x7E1D,0x7E3E,0x7E5F,0x7E7E,
????0x7E9C,0x7EB9,0x7ED5,0x7EEF,0x7F09,0x7F21,0x7F37,0x7F4D,
????0x7F61,0x7F74,0x7F86,0x7F97,0x7FA6,0x7FB4,0x7FC1,0x7FCD,
????0x7FD8,0x7FE1,0x7FE9,0x7FF0,0x7FF5,0x7FF9,0x7FFD,0x7FFE}
const?int16_t?hSin_Cos_Table[256]?=?SIN_COS_TABLE;
typedef?struct
{
??int16_t?hCos;
??int16_t?hSin;
}?Trig_Components;
/**
??*?@brief??This?function?returns?cosine?and?sine?functions?of?the?angle?fed?in
??*?????????input
??*?@param??hAngle:?angle?in?q1.15?format?(-1~0.9999)
??*?@retval?Trig_Components?Cos(angle)?and?Sin(angle)?in?Trig_Components?format
??*/
Trig_Components?trig_functions(?int16_t?hAngle?)
{
?int32_t?shindex;
?uint16_t?uhindex;
?Trig_Components?Local_Components;
?/*?10?bit?index?computation??*/
?shindex?=?(?(?int32_t?)32768?+?(?int32_t?)hAngle?);
?uhindex?=?(?uint16_t?)shindex;
?//uhindex?/=?(?uint16_t?)64;
????uhindex?=?uhindex?>>?6;
?/**
??|?hAngle????|?angle??|?std???|
??|?(0,16384]???|?U0_90??|?(0,0.5]?|
??|?(16384,32767]??|?U90_180??|?(0.5,0.99]|
??|?(-16384,-1]???|?U270_360??|?(0,-0.5]??|
??|?(-16384,-32768]?|?U180_270??|?(-0.5,-1)?|
?*/
//SIN_MASK????????0x0300u
?switch?(?(?uint16_t?)(?uhindex?)?&?SIN_MASK?)
?{??????????
//0x0200u
???case?U0_90:
??Local_Components.hSin?=?
????????????hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??Local_Components.hCos?=?
????????????hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??break;
//0x0300u
???case?U90_180:
??Local_Components.hSin?=?
????????????hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??Local_Components.hCos?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??break;
//0x0000u
???case?U180_270:
??Local_Components.hSin?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??Local_Components.hCos?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??break;
//0x0100u
???case?U270_360:
??Local_Components.hSin?=??
????????????-hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??Local_Components.hCos?=??
????????????hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??break;
???default:
??break;
?}
?return?(?Local_Components?);
}
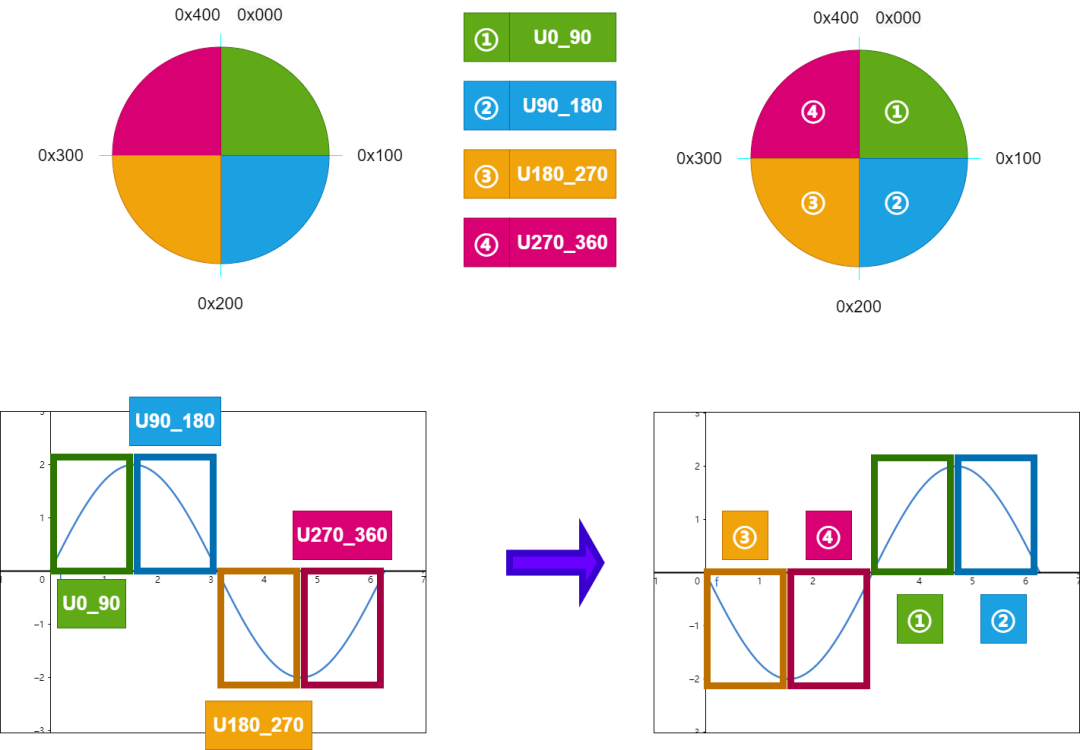
由于輸入的hAngle是Q1.15格式,所以這里可以簡單畫個圖;下面是角度hAngle從0x0000~0xFFFF的示意圖,如下所示;
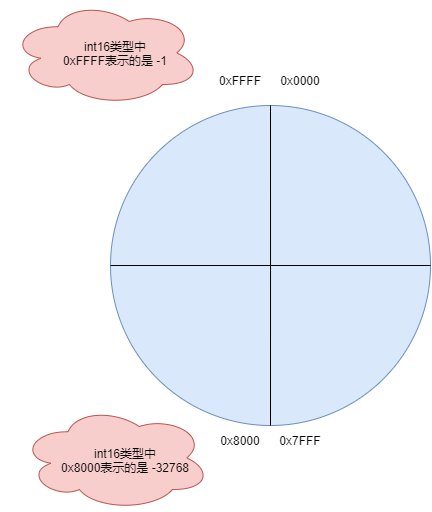 角度值
角度值這里注意,負數是以補碼形式進行保存的,正數的補碼等于他本身;
負數的補碼是除了符號位外,其他位取反,然后加上1;
所以可以算一下
0xFFFF表示-1;
0x8000表示-32768;
因為Q格式中有無符號的范圍和帶符號的范圍,所以這里的hAngle充分利用這個16 bit的數據,并且兼容了傳入參數可以是有符號int16或者是無符號uint16,這里比較繞,先看下面這張圖片;
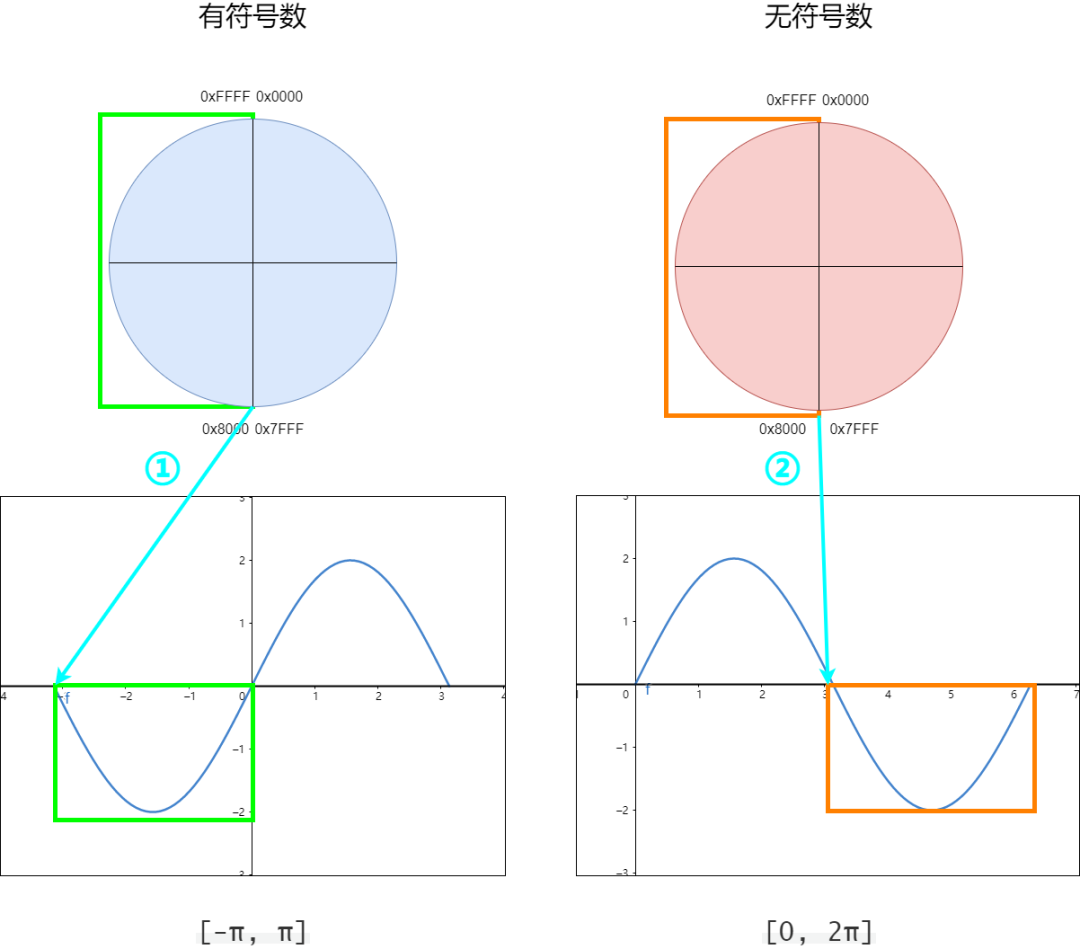 有符號和無符號 對比
有符號和無符號 對比上圖中;
-
左邊是有符號
int16,右邊是無符號數uint16; -
兩個圓形分別表示
int16和uint16的數值范圍; - 左邊綠色框內的波形相對應,橙色框內的波形相對應;
這里有幾點我們要注意一下,無論是有符號和無符號,他們的周期都是相同的;
- 有符號整數 int16 :-32768 ~ 32765 ,
- 無符號整數 uint16 :0 ~ 65535,
所以這兩者都使用 65536個數來表示正弦的一個周期,也就是 2π。
這里是比較關鍵的地方,因此對于?0x8000 這個關鍵點,有符號和無符號所表示的數值是不同的;
- 有符號整數 int16 :0x8000 表示為 -32768;
- 無符號整數 uint16 :0x8000 表示為 32768;
因此這他們剛好相差了一個周期 65536,所以表示的正弦數值y是相同的,正如上圖中藍色箭頭①和②所示。
內部實現
由于有符號整數 int16 的最高位是符號位,所以這里我們先把它轉化成無符號整形;
前面用 int32類型是為了防止數據溢出,這里加上32768,相當于對正弦波平移了半個周期,所以在下面y和x的映射關系需要根據實際情況來修改;
/*?10?bit?index?computation??*/
shindex?=?(?(?int32_t?)32768?+?(?int32_t?)hAngle?);
uhindex?=?(?uint16_t?)shindex;
//uhindex?/=?(?uint16_t?)64;
uhindex?=?uhindex?>>?6;
因為前面提高過正弦表的四分之一是256個數據,所以整個正弦周期應該是 1024 個細分數據,那也就是2的10次,就需要?10 bit;
-
10 bit的數據范圍是0~1023; -
16 bit的數據范圍是0~65535;
為了獲取有效的高10 bit數據,對數據右移 6 bit,具體如下所示;
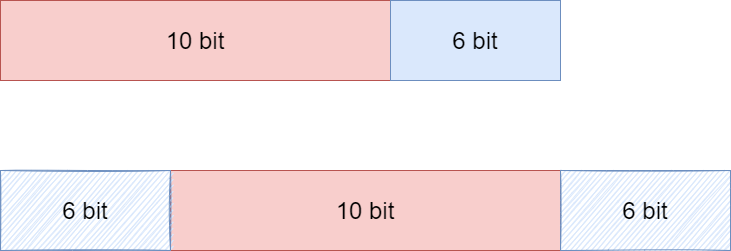
所以,我們又可以得到以下這個數據的范圍 0 ~ 1023 ,0 ~ 0x400
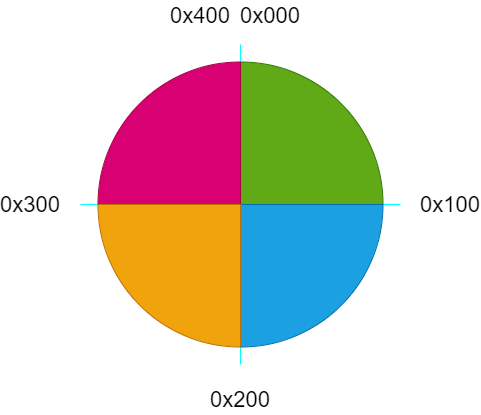
因此我們在程序中引入四個掩碼,作為正弦波形落在哪個象限的標識位,這樣也避免了使用除法運算,提高了效率,具體如下所示;
#define?SIN_MASK????????0x0300u
#define?U0_90???????????0x0200u
#define?U90_180?????????0x0300u??????????????????
#define?U180_270????????0x0000u
#define?U270_360????????0x0100u
其中,U0_90表示 0° ~ 90°,以此類推;
那為什么是這個映射關系呢?
0~90°不應該是從 0x000u~0x100u嗎?這里我們再簡單解釋一下;
前面有一個這樣的操作,具體如下;
shindex?=?(?(?int32_t?)32768?+?(?int32_t?)hAngle?);
uhindex?=?(?uint16_t?)shindex;
這里的hAngle加上32768,相當于加了一個π,正弦波形向左移動了半個周期;因此整體的映射關系要和原始的數據對應起來,具體如下所示;
?
最后,既然我們已經知道波形在哪個象限了,就可以根據當前象限和我們正弦表的關系來得到新的波形,這里有中心對稱,關于y軸對稱,簡單做一下變換就可以得到正弦值和余弦值;
//SIN_MASK????????0x0300u
?switch?(?(?uint16_t?)(?uhindex?)?&?SIN_MASK?)
?{??????????
//0x0200u
???case?U0_90:
??Local_Components.hSin?=?
????????????hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??Local_Components.hCos?=?
????????????hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??break;
//0x0300u
???case?U90_180:
??Local_Components.hSin?=?
????????????hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??Local_Components.hCos?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??break;
//0x0000u
???case?U180_270:
??Local_Components.hSin?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??Local_Components.hCos?=?
????????????-hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??break;
//0x0100u
???case?U270_360:
??Local_Components.hSin?=??
????????????-hSin_Cos_Table[(?uint8_t?)(?0xFFu?-?(?uint8_t?)(?uhindex?)?)];
??Local_Components.hCos?=??
????????????hSin_Cos_Table[(?uint8_t?)(?uhindex?)];
??break;
???default:
??break;
?}
??
 電子發燒友App
電子發燒友App





















評論