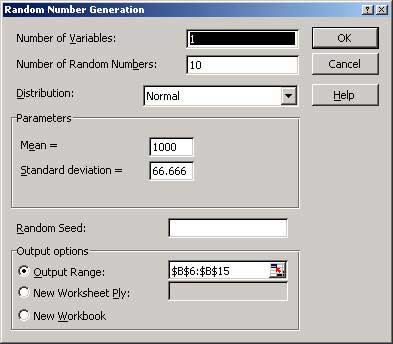
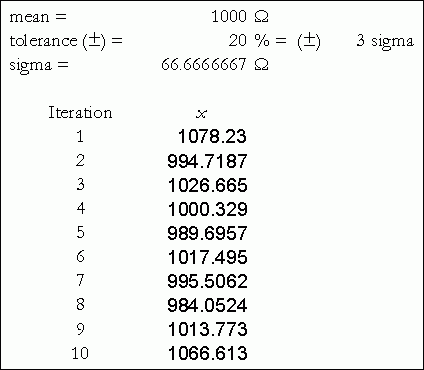
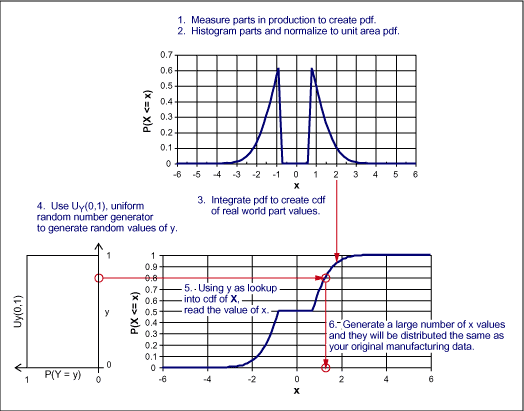
本文中,我們了解了如何生成良率分析所使用的隨機(jī)組件值。對(duì)于許多常見分布來說,Excel提供了一些讓這一過程更加快速、簡(jiǎn)單的內(nèi)置函數(shù)。
2011-01-14 10:03:24 4828
4828 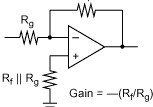
使用簡(jiǎn)化的DC-DC轉(zhuǎn)換器模型,分析了三個(gè)變量,兩個(gè)反饋電阻和內(nèi)部基準(zhǔn)電壓源用于對(duì)電壓設(shè)定點(diǎn)調(diào)節(jié)進(jìn)行建模。使用統(tǒng)計(jì)分析,給出了最終的電壓設(shè)定點(diǎn)分布。結(jié)果以圖形方式繪制。這與最壞情況的計(jì)算相比。由此產(chǎn)生的數(shù)據(jù)表明,最壞情況限制在統(tǒng)計(jì)上是不可能的。
2022-12-15 14:22:31 2498
2498 LTspice?可用于對(duì)復(fù)雜電路進(jìn)行統(tǒng)計(jì)容差分析。本文介紹在LTspice中使用蒙特卡羅和高斯分布進(jìn)行容差分析和最差情況分析的方法。
2022-03-08 10:52:36 3670
3670 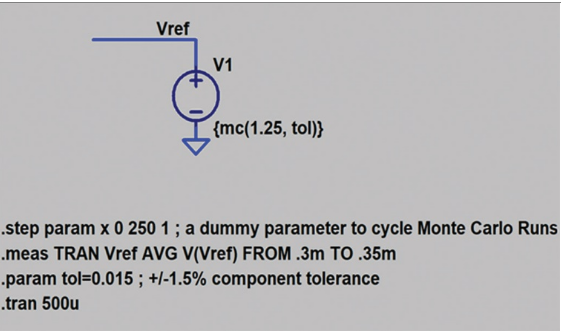
EXCEL統(tǒng)計(jì)涵數(shù)示例
2009-06-01 17:49:51
................................................................................................................................8七、統(tǒng)計(jì)分析仿真.......................................................................................................................9[hide][/hide]
2009-09-28 12:36:41
本帖最后由 gk320830 于 2015-3-7 19:50 編輯
LED恒流驅(qū)動(dòng)電路的設(shè)計(jì)分析與實(shí)例.
2012-08-01 20:15:40
仿真電路性能,利用蒙特卡羅和高斯分布來體現(xiàn)參數(shù)容差變化,并將其與最差情況分析仿真進(jìn)行比較。除了提到的關(guān)于最差情況分析的一些問題外,最差情況分析和統(tǒng)計(jì)分析都能提供與系統(tǒng)設(shè)計(jì)相關(guān)的寶貴見解。關(guān)于如何在
2022-03-25 10:52:10
MATLAB語言與現(xiàn)代科學(xué)計(jì)算1 數(shù)值線性代數(shù)問題2 數(shù)值微積分3 數(shù)據(jù)插值與統(tǒng)計(jì)分析4 數(shù)學(xué)問題的解析運(yùn)算與高精度運(yùn)算5 例子與習(xí)題[hide][/hide]
2009-09-04 08:20:03
(時(shí)間偏差)來評(píng)估的。 我們通過專用的TestManagerPro數(shù)據(jù)分析軟件,可對(duì)測(cè)試記錄進(jìn)行專業(yè)的數(shù)據(jù)分析及模板比對(duì),統(tǒng)計(jì)分析時(shí)鐘同步信號(hào)的長(zhǎng)期漂移性能,可計(jì)算MTIE、TDEV,并按照G.811、G.812、G.813、G.823、G.8261等模板進(jìn)行比對(duì),并生成測(cè)試報(bào)表。`
2015-01-19 17:36:11
[MATLAB統(tǒng)計(jì)分析與應(yīng)用:40個(gè)案例分析].謝中華.掃描版
2017-10-31 12:20:40
創(chuàng)始人之一,編著書籍《MATLAB統(tǒng)計(jì)分析與應(yīng)用:40個(gè)案例分析》。現(xiàn)于天津科技大學(xué)數(shù)學(xué)系任教,長(zhǎng)期從事本科生《概率論與數(shù)理統(tǒng)計(jì)》、《多元統(tǒng)計(jì)分析》,碩士研究生《數(shù)理統(tǒng)計(jì)》,博士研究生《應(yīng)用數(shù)學(xué)
2011-04-19 10:43:41
采集時(shí)信號(hào)的波形、基本統(tǒng)計(jì)參數(shù)實(shí)時(shí)顯示以文件方式實(shí)時(shí)存儲(chǔ)信號(hào),從文件中讀取數(shù)據(jù)并具有如下分析功能 1.信號(hào)的統(tǒng)計(jì)分析功能2。信號(hào)相關(guān)分析功能3.頻譜分析功能4.可自定義參數(shù)的數(shù)字濾波功能
2014-12-24 19:14:48
`一個(gè)實(shí)用的例子——統(tǒng)計(jì)分析`
2013-05-07 09:14:33
一個(gè)隨機(jī)數(shù) 統(tǒng)計(jì)分析 的范例程序
2015-02-28 14:19:05
是對(duì)隨機(jī)信號(hào)進(jìn)行統(tǒng)計(jì)分析。對(duì)信號(hào)的時(shí)域統(tǒng)計(jì)分析,可以求得信號(hào)的均值、均方值、方差、概率密度函數(shù)等,也包括對(duì)確定性周期信號(hào)的各種強(qiáng)度進(jìn)行分析。gooxian.com1.周期信號(hào)的強(qiáng)度周期信號(hào)的強(qiáng)度以峰值、絕對(duì)
2017-12-05 10:59:24
人員;)BOM管理導(dǎo)入BOM,查看BOM,導(dǎo)出BOMBOM比較支持不同版本的設(shè)計(jì)BOM清單差異分析,對(duì)設(shè)計(jì)完成的BOM進(jìn)行比對(duì)及物料選型校驗(yàn),支持導(dǎo)出效驗(yàn)報(bào)告BOM統(tǒng)計(jì)分析支持器件成本統(tǒng)計(jì)分析(按PCB
2022-05-16 11:08:22
有誰有看過謝中華編的《matlab統(tǒng)計(jì)分析與應(yīng)用:40個(gè)案例分析》這本書啊?謝謝!
2013-02-26 15:00:42
圖解隱馬爾可夫模型(HMM)
2019-08-20 14:17:43
Hive: 可以對(duì)數(shù)據(jù)轉(zhuǎn)換為類SQL執(zhí)行,調(diào)用hadoop mapreduce進(jìn)行分布式計(jì)算。據(jù)說facebook的95%統(tǒng)計(jì)分析由此進(jìn)行。有了分布式后ad hoc查詢也變成可能。所以該軟件還是不錯(cuò)的。
2019-07-15 06:34:12
珠三角還有什么電子組裝大賽么?要給信息管理畢業(yè)的妹紙來做電子行業(yè)統(tǒng)計(jì)分析 好愁苦。
2013-07-16 01:10:20
參考點(diǎn),這是測(cè)量的關(guān)鍵點(diǎn)之一。在示波器里,一般稱為:Vtop和Vbase。Vtop和Vbase的測(cè)量計(jì)算是:采用幅度統(tǒng)計(jì)方法。示波器的工作過程是:先對(duì)整個(gè)屏幕進(jìn)行幅度統(tǒng)計(jì)分析,可以得出最大電壓的位置
2019-05-17 14:28:23
中央空調(diào)節(jié)能按第一節(jié)概況內(nèi)容中圖表統(tǒng)計(jì)分析,系統(tǒng)負(fù)載率在50%以下的時(shí)間占全部運(yùn)行時(shí)間的50%以上,滿負(fù)荷的機(jī)會(huì)不多,若采用普通常規(guī)的控制系統(tǒng),中央空調(diào)系統(tǒng)的水泵、冷卻塔必須全天運(yùn)行,能源浪費(fèi)很大
2021-09-09 06:47:57
的形式根據(jù)客戶需求自由配置任意類型和數(shù)量的測(cè)頭、傳感器、串口繼電器、電機(jī)驅(qū)動(dòng)器、旋轉(zhuǎn)編碼器等傳感器、控制器和執(zhí)行器。 軟件系統(tǒng)其一: 在數(shù)據(jù)統(tǒng)計(jì)分析方面,軟件可針對(duì)任意一個(gè)或多個(gè)測(cè)量值做統(tǒng)計(jì)分析,并
2019-01-16 10:40:33
請(qǐng)問ThreadX原裝任務(wù)統(tǒng)計(jì)分析功能怎么實(shí)現(xiàn)?
2021-11-30 07:23:28
選擇ADE L進(jìn)入仿真設(shè)置界面,在Model Libraries中選中mc 但是在tools下或其他地方找不到MonteCarlo分析或統(tǒng)計(jì)分析選項(xiàng)。在此請(qǐng)過來人賜教阿,謝謝!
2021-06-25 06:42:25
給大家分享一份整理好的LED背光驅(qū)動(dòng)電路設(shè)計(jì)分析資料需要的朋友點(diǎn)擊下載喲↓
2016-01-28 15:10:45
在信號(hào)的分析與處理中常常需要用到不少數(shù)學(xué)基礎(chǔ)知識(shí),因此在本章中將對(duì)統(tǒng)計(jì)信號(hào)處理中可能用到的數(shù)學(xué)知識(shí)做簡(jiǎn)單的回顧。第一節(jié)主要是對(duì)概率論內(nèi)容的概述;第二節(jié)主要是
2008-09-05 11:15:09 42
42 主要特點(diǎn)卓越的動(dòng)態(tài)范圍和精度高分辨率模式最高的測(cè)量速度自動(dòng)脈沖分析統(tǒng)計(jì)分析
2022-03-23 17:56:06
主要特點(diǎn)卓越的動(dòng)態(tài)范圍和精度高分辨率模式最高的測(cè)量速度自動(dòng)脈沖分析統(tǒng)計(jì)分析
2022-03-23 18:02:52
畢業(yè)論文的題目為:石英晶體諧振器的生產(chǎn)過程的統(tǒng)計(jì)分析。論文通過對(duì)一些控制圖表的運(yùn)用來分析不合格產(chǎn)品的失效原因,從而實(shí)現(xiàn)產(chǎn)品的生產(chǎn)過程的控制。本篇論文主要考
2008-11-24 17:06:24 29
29 摘要:作為大規(guī)模生產(chǎn)的電子元器件,石英晶體諧振器的生產(chǎn)過程不可避免的涉及到大量的統(tǒng)計(jì)分析。最基本的要求是統(tǒng)計(jì)生產(chǎn)過程的成品率,但我們往往可以結(jié)合數(shù)據(jù)的采集和
2008-11-24 21:40:03 41
41 針對(duì)目前廣泛使用的最低比特位(LSB)信息隱藏算法容易被基于統(tǒng)計(jì)檢測(cè)的隱寫分析方法如RS分析或X2分析等檢測(cè)出來,提出一種新型的LSB隱寫算法,能有效地抵抗基于統(tǒng)計(jì)檢測(cè)的隱寫
2009-04-09 09:57:31 12
12 話務(wù)統(tǒng)計(jì)分析的作用:能夠通過話務(wù)統(tǒng)計(jì)來觀察一個(gè)整體網(wǎng)絡(luò)性能的平均水平能夠通過話務(wù)統(tǒng)計(jì)來發(fā)現(xiàn)網(wǎng)絡(luò)中的故障問題能夠通過話務(wù)統(tǒng)計(jì)來對(duì)網(wǎng)絡(luò)性能進(jìn)行優(yōu)化話務(wù)統(tǒng)計(jì)
2009-06-19 17:45:29 19
19 旁路分析可以繞過對(duì)加解密算法的繁瑣的分析,通過分析泄漏的信號(hào)而獲取芯片密碼信息。其關(guān)鍵問題在于掌握芯片運(yùn)行過程中泄漏信息的機(jī)理,進(jìn)而建立統(tǒng)計(jì)分析泄漏信號(hào)的信
2009-08-24 11:05:45 11
11 本文提出一種基于PSpice 的參數(shù)掃描分析、優(yōu)化分析和蒙特卡羅統(tǒng)計(jì)分析相結(jié)合的方法對(duì)電子電路進(jìn)行最優(yōu)化設(shè)計(jì),可以有效地提高電路設(shè)計(jì)的準(zhǔn)確性
2009-09-05 09:00:20 82
82 入侵檢測(cè)在當(dāng)今網(wǎng)絡(luò)安全技術(shù)中發(fā)揮越來越重要的作用,統(tǒng)計(jì)分析作為其中的一種研究方法得廣泛的應(yīng)用。本文從IDES 著手,將統(tǒng)計(jì)分析技術(shù)對(duì)
2009-09-14 09:16:13 22
22 結(jié)合分布式票房數(shù)據(jù)綜合統(tǒng)計(jì)分析系統(tǒng)(SSOB)的設(shè)計(jì),利用數(shù)據(jù)庫復(fù)制等技術(shù),構(gòu)建基于Web 分布式系統(tǒng)的數(shù)據(jù)采集、匯總、統(tǒng)計(jì)系統(tǒng)的問題。介紹了系統(tǒng)的設(shè)計(jì)思想、系統(tǒng)體系結(jié)構(gòu)
2009-09-23 10:57:54 21
21 結(jié)合分布式票房數(shù)據(jù)綜合統(tǒng)計(jì)分析系統(tǒng)(SSOB)的設(shè)計(jì),利用數(shù)據(jù)庫復(fù)制等技術(shù),構(gòu)建基于Web 分布式系統(tǒng)的數(shù)據(jù)采集、匯總、統(tǒng)計(jì)系統(tǒng)的問題。介紹了系統(tǒng)的設(shè)計(jì)思想、系統(tǒng)體系結(jié)構(gòu)
2009-09-24 16:25:05 4
4 SPSS 統(tǒng)計(jì)分析軟件在氣、水層識(shí)別中的應(yīng)用:本文結(jié)合測(cè)井、錄井、完井測(cè)試等資料的氣、水顯示情況,選取新場(chǎng)地區(qū)某氣藏典型井,使用統(tǒng)計(jì)軟件SPSS進(jìn)行逐步判別分析,建立該地區(qū)
2009-10-19 21:04:57 18
18 對(duì)變壓器油進(jìn)行各項(xiàng)測(cè)試和分析,是監(jiān)測(cè)變壓器安全運(yùn)行的一種最經(jīng)濟(jì)有效的方式通過對(duì)110kV整流變壓器油質(zhì)各項(xiàng)測(cè)試數(shù)據(jù)的統(tǒng)計(jì)分析,可綜合評(píng)價(jià)油的整體質(zhì)量,迅速分析存在的問
2010-01-14 15:52:26 30
30 質(zhì)量管理與統(tǒng)計(jì)分析何謂質(zhì)量管理質(zhì)量管理英文譯為Quality Control,取其第一個(gè)字母,稱為QC,近年來稱為質(zhì)量管理,英文譯為Quality Management,簡(jiǎn)稱QM,如下加以定義。「為
2010-01-30 16:19:56 49
49 提出統(tǒng)計(jì)分析系統(tǒng)不應(yīng)該歸入普通管理信息系統(tǒng),而應(yīng)該根據(jù)用戶具體需求,充分分析其本質(zhì),利用數(shù)據(jù)倉庫技術(shù)進(jìn)行開發(fā)和實(shí)現(xiàn),并闡述了如何利用數(shù)據(jù)倉庫技術(shù)從需求分析到最
2010-09-07 10:09:00 9
9 方差分析方差分析是從方差的角度分析試驗(yàn)數(shù)據(jù)、鑒定各因素作用大小的有效的統(tǒng)計(jì)分析方法。其主要特點(diǎn)是能夠把各因素的影響、試驗(yàn)條件改變形成的效應(yīng)和隨機(jī)誤差,從總的
2010-10-02 10:46:28 0
0 實(shí)驗(yàn)結(jié)果統(tǒng)計(jì)分析與實(shí)驗(yàn)論文寫作
1.實(shí)驗(yàn)結(jié)果統(tǒng)計(jì)分析1.1 愈傷組織誘導(dǎo)
編號(hào)
2009-02-17 16:26:41 4756
4756 實(shí)驗(yàn)二 機(jī)械加工精密的統(tǒng)計(jì)分析一、實(shí)驗(yàn)?zāi)康?. 學(xué)會(huì)用點(diǎn)圖法研究被加工零件尺寸的變化規(guī)律和控制被加工零件尺寸。2. 驗(yàn)證已調(diào)整好的機(jī)床上加工一批零
2009-03-17 10:21:20 1308
1308 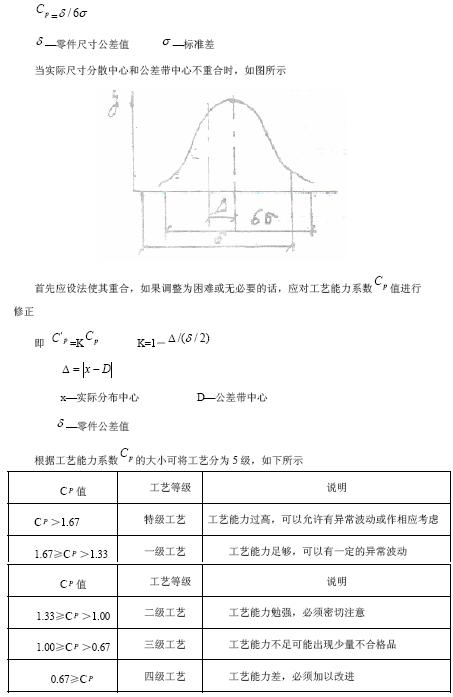
一直以來, SAS公司的JMP軟件都特別地將交互式圖形和內(nèi)置的強(qiáng)大統(tǒng)計(jì)分析功能相結(jié)合,提供強(qiáng)大、高效的統(tǒng)
2010-12-31 08:58:39 1939
1939 利用Excel進(jìn)行電
2011-01-07 17:56:18 0
0 EDA與VHDL的實(shí)用電路模塊設(shè)計(jì)分析
2011-03-02 16:57:46 0
0 功耗已經(jīng)成為 集成電路 設(shè)計(jì)的一個(gè)十分重要的問題=對(duì)于一個(gè)給定的電路,其功耗是與輸入密切相關(guān)的,即對(duì)于不同的輸入向量集,同一電路可能會(huì)有不同的功耗=功耗敏感性定義了由于
2011-06-29 18:12:18 20
20 電路容差統(tǒng)計(jì)分析包括蒙特卡羅分析靈敏度分析和最壞情況分析研究了蒙特卡羅分析的技巧程序語句參數(shù)的設(shè)置輸出結(jié)果的判讀等并應(yīng)用Pspice 對(duì)實(shí)例電路進(jìn)行特性仿真
2011-08-23 16:18:58 68
68 采用樣板機(jī)法計(jì)算風(fēng)電場(chǎng)棄風(fēng)電量的實(shí)測(cè)數(shù)據(jù)統(tǒng)計(jì)分析_丁坤
2016-12-29 14:40:19 2
2 ICE超聲圖像斑點(diǎn)噪聲的統(tǒng)計(jì)分析_李軼鵬
2017-01-07 16:00:43 0
0 統(tǒng)計(jì)分析
2017-02-07 17:11:29 0
0 云計(jì)算統(tǒng)監(jiān)控與 復(fù)雜事件處理 是一個(gè)基于 Linux 平臺(tái)的 統(tǒng)計(jì)分析 框架 。它 是一 個(gè)集數(shù)據(jù)采,傳輸和統(tǒng)計(jì)分析于一體的應(yīng)用系框架 集數(shù)據(jù)采,傳輸和統(tǒng)計(jì)分析于一體的應(yīng)用系框架 ,并且支持對(duì)大數(shù)
2017-10-09 09:54:40 10
10 在煉鋼過程中配料、上料過程將直接影響鋼的產(chǎn)量及質(zhì)量,如果能對(duì)這一過程進(jìn)行記錄分析,將有利于工藝的改進(jìn)及分析產(chǎn)生次品的原因。下面就講解一下通過紫金橋?qū)崟r(shí)數(shù)據(jù)庫實(shí)現(xiàn)配料、上料過程記錄分析的方法和過程。
2017-10-13 10:02:05 22
22 為了解決睡眠節(jié)律研究中數(shù)據(jù)的快速導(dǎo)入、準(zhǔn)確分析和詳細(xì)統(tǒng)計(jì)的問題,提出了一種睡眠節(jié)律數(shù)據(jù)統(tǒng)計(jì)分析系統(tǒng)。該系統(tǒng)基于.NET開發(fā)平臺(tái),以O(shè)racle為后臺(tái)數(shù)據(jù)庫,采用B/S結(jié)構(gòu)模式,分為數(shù)據(jù)導(dǎo)入分析和查詢
2017-11-15 16:22:24 8
8 本文介紹了質(zhì)量檢驗(yàn)的基本概念,詳述了統(tǒng)計(jì)抽樣檢驗(yàn)以及質(zhì)量統(tǒng)計(jì)與質(zhì)量統(tǒng)計(jì)分析等相關(guān)技術(shù)的詳解。
2017-11-20 14:06:29 35
35 了接收機(jī)正常接收信號(hào)模型和欺騙信號(hào)入侵后接收信號(hào)模型,對(duì)真實(shí)信號(hào)與欺騙信號(hào)的復(fù)合信號(hào)的統(tǒng)計(jì)規(guī)律進(jìn)行了分析。理論分析表明,當(dāng)欺騙信號(hào)與真實(shí)信號(hào)存在頻差時(shí),檢測(cè)算法能夠通過I路信號(hào)的幅度變化檢測(cè)出欺騙信號(hào)。仿真結(jié)果
2017-11-28 16:39:42 0
0 統(tǒng)計(jì)分析日志數(shù)據(jù)并將結(jié)果指導(dǎo)決策能夠提高企業(yè)的競(jìng)爭(zhēng)力。因此最原始的日志數(shù)據(jù)記錄具有豐富和巨大的價(jià)值。 目前很多開源的系統(tǒng),如Flume、Kalka、Storm、HBase等可以對(duì)日志數(shù)據(jù)進(jìn)行處理,但是這些系統(tǒng)相互獨(dú)立,均龐大復(fù)雜,需要專門
2017-11-30 10:49:15 0
0 針對(duì)程序切片方法不提供語句的可疑程度描述,而覆蓋分析方法不能充分分析程序元素間的相互影響等問題,提出上下文統(tǒng)計(jì)分析的軟件故障定位方法。首先,將源程序轉(zhuǎn)換為抽象語法樹和程序依賴圖;接下來,插樁程序
2018-01-16 17:25:20 0
0 統(tǒng)計(jì)分析風(fēng)電機(jī)組間的風(fēng)速相關(guān)性對(duì)風(fēng)電場(chǎng)的等值建模、風(fēng)速/風(fēng)功率預(yù)測(cè)及機(jī)組集群控制優(yōu)化均具有指導(dǎo)意義。鑒于風(fēng)電機(jī)組間的風(fēng)速相關(guān)性研究工作開展較少,首先構(gòu)建基于風(fēng)電機(jī)組輸出功率為索引的風(fēng)電機(jī)組實(shí)際運(yùn)行
2018-01-16 18:25:47 0
0 隨著風(fēng)電滲透率的逐漸增加,超短期風(fēng)電功率爬坡事件對(duì)電力系統(tǒng)的影響愈來愈顯著。當(dāng)前國(guó)內(nèi)對(duì)爬坡事件沒有明確定義,且缺少相應(yīng)的檢測(cè)方法和統(tǒng)計(jì)分析。闡述了爬坡事件的定義,提出了一種超短期風(fēng)電功率爬坡事件檢測(cè)
2018-04-03 14:41:35 0
0 有人對(duì)比較成功的17款電動(dòng)汽車做了統(tǒng)計(jì),結(jié)果表明8款采用了方形卷繞式,7款采用了方形層疊式,2款采用了圓柱卷繞式。電動(dòng)汽車在選擇電池構(gòu)型上的分歧,實(shí)質(zhì)上也反映了這些構(gòu)型各具優(yōu)、缺點(diǎn)。
2018-04-10 17:30:10 16979
16979 
3.1 誤差分析背后的統(tǒng)計(jì)學(xué)知識(shí)
2018-08-22 01:32:00 4582
4582 半導(dǎo)體器件及電路的性能會(huì)因?yàn)楣に嚤旧砉逃械幕?b class="flag-6" style="color: red">統(tǒng)計(jì)性變異 (statistical variation)而發(fā)生波動(dòng)。
2018-12-18 08:55:00 4106
4106 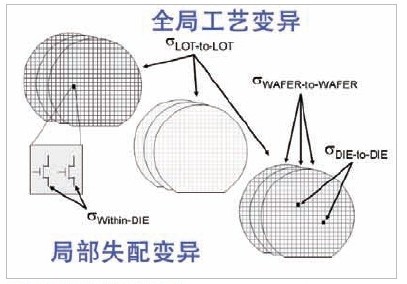
新的英特爾?數(shù)據(jù)分析加速庫(英特爾?DAAL)可加速數(shù)據(jù)處理,用于數(shù)據(jù)挖掘,統(tǒng)計(jì)分析和機(jī)器學(xué)習(xí)。
2018-11-07 06:31:00 2164
2164 3.3 使用蒙特卡羅SPICE工具進(jìn)行誤差統(tǒng)計(jì)分析
2019-04-12 06:10:00 3401
3401 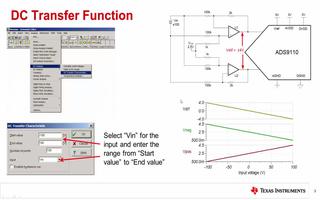
商業(yè)競(jìng)爭(zhēng)日益激烈,如何合理地分配和管理門店資源至關(guān)重要,而科學(xué)準(zhǔn)確的客流統(tǒng)計(jì)分析有利于門店可以更好地經(jīng)營(yíng),制定更有效的營(yíng)銷活動(dòng)。客流統(tǒng)計(jì)解決方案,實(shí)現(xiàn)門店動(dòng)態(tài)人數(shù)統(tǒng)計(jì),掌握實(shí)際總客流量和客流規(guī)律,更好地進(jìn)行門店資源配置。
2019-11-05 16:03:03 1248
1248 
本文檔的主要內(nèi)容詳細(xì)介紹的是使用OrCAD PSpice實(shí)現(xiàn)放大電路的設(shè)計(jì)分析。
2019-12-24 14:54:00 37
37 線性回歸是利用數(shù)理統(tǒng)計(jì)中回歸分析,來確定兩種或兩種以上變量間相互依賴的定量關(guān)系的一種統(tǒng)計(jì)分析方法,運(yùn)用十分廣泛。其表達(dá)形式為y = w’x+e,e為誤差服從均值為0的正態(tài)分布。
2020-01-23 17:33:00 2567
2567 
通過對(duì)故障錄波圖的分析,找出事故原因,分析繼電保護(hù)裝置的動(dòng)作作為,對(duì)故障性質(zhì)及概率進(jìn)行科學(xué)的統(tǒng)計(jì)分析,統(tǒng)計(jì)分析系統(tǒng)振蕩時(shí)有關(guān)參數(shù)。
2019-12-31 09:46:55 2059
2059 電 壓采樣的問題:這里的問題在前面也談過,由于受電阻誤差,AD口漏電流,AD的采樣誤差,AD的參考電壓等因素的影響,會(huì)產(chǎn)生誤差。這里采樣的精度大概為 8%左右。
2020-03-15 17:29:00 1999
1999 本文檔的主要內(nèi)容詳細(xì)介紹的是數(shù)學(xué)建模算法與應(yīng)用的學(xué)習(xí)課件資料合集免費(fèi)下載包括了: 線性規(guī)劃,整數(shù)規(guī)劃,非線性規(guī)劃,非線性規(guī)劃, Excel在統(tǒng)計(jì)分析與數(shù)量方法中的應(yīng)用,SPSS在統(tǒng)計(jì)分析中的應(yīng)用,Matlab在線性代數(shù)中的應(yīng)用,支持向量機(jī)等等。
2020-04-09 08:00:00 8
8 停止條件即示波器停止“統(tǒng)計(jì)分析”的條件,當(dāng)測(cè)試條件滿足預(yù)設(shè)條件時(shí),時(shí)序分析軟件會(huì)停止統(tǒng)計(jì)完成分析工作。
2020-04-29 15:18:52 2425
2425 校園考勤管理需要支持考勤數(shù)據(jù)統(tǒng)計(jì)分析功能的需求,支持學(xué)校宿舍每一間考勤數(shù)據(jù)進(jìn)行統(tǒng)計(jì),并以圖形化的界面展現(xiàn)統(tǒng)計(jì)結(jié)果,并且可以根據(jù)時(shí)間查詢宿舍考勤數(shù)據(jù),支持導(dǎo)出考勤數(shù)據(jù)等宿舍相關(guān)業(yè)務(wù)管理功能。
2020-09-20 10:49:02 4651
4651 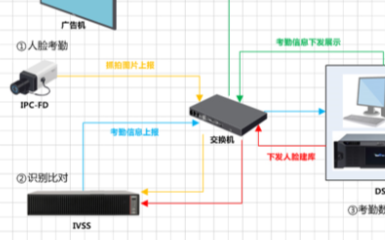
電子發(fā)燒友網(wǎng)為你提供鼎利5G統(tǒng)計(jì)分析指導(dǎo)書資料下載的電子資料下載,更有其他相關(guān)的電路圖、源代碼、課件教程、中文資料、英文資料、參考設(shè)計(jì)、用戶指南、解決方案等資料,希望可以幫助到廣大的電子工程師們。
2021-04-22 08:42:52 6
6 多元統(tǒng)計(jì)分析:R與Python的實(shí)現(xiàn)說明。
2021-05-27 11:27:41 7
7 基于假設(shè)檢驗(yàn)理論的信號(hào)統(tǒng)計(jì)分辨研究
2021-06-18 10:50:29 5
5 ,就不得不說這個(gè)數(shù)據(jù)分析利器——Excel函數(shù),也是Excel最主要的功能之一。 Excel中的函數(shù)指的是一些系統(tǒng)預(yù)定義的公式,通過輸入?yún)?shù)值即可進(jìn)行函數(shù)對(duì)應(yīng)功能的計(jì)算,且函數(shù)名與功能基本對(duì)應(yīng),也比較好記。 需要區(qū)分的是,本章提及的“函數(shù)”,指的是Excel軟件中實(shí)現(xiàn)某
2021-08-17 16:43:47 3024
3024 
統(tǒng)計(jì)分數(shù)并分級(jí)文章目錄題目重述問題分析以及求解思路程序代碼題目重述某系有20名學(xué)生參加外語統(tǒng)考,假設(shè)成績(jī)已經(jīng)存放在RAM地址為ENGLISH的連續(xù)存儲(chǔ)單元中,現(xiàn)決定給成績(jī)?cè)?0100分之間的學(xué)生頒發(fā)
2021-11-25 12:21:07 0
0 數(shù)據(jù)分析,指應(yīng)用適當(dāng)?shù)?b class="flag-6" style="color: red">統(tǒng)計(jì)分析方法對(duì)收集到的海量數(shù)據(jù)進(jìn)行分析,并將這些數(shù)據(jù)加以匯總、理解、消化,以求最大化地挖掘蘊(yùn)含在數(shù)據(jù)中的價(jià)值,發(fā)揮數(shù)據(jù)的作用。
2021-12-01 14:50:38 2962
2962 l 設(shè)備管理
l 風(fēng)險(xiǎn)評(píng)估
l 作業(yè)管理
l 行為管理
l 授權(quán)管理
l 統(tǒng)計(jì)分析管理
2021-12-22 14:01:27 1296
1296 所謂專利信息分析,是指通過對(duì)專利信息進(jìn)行加工整理,分析形成專利競(jìng)爭(zhēng)情報(bào),并針對(duì)其中的著錄項(xiàng)、技術(shù)信息和權(quán)利信息進(jìn)行組合統(tǒng)計(jì)分析,整理出直觀易懂的結(jié)果,并以圖表的形式展現(xiàn)出來。與此同時(shí),技術(shù)人員通過對(duì)報(bào)告間信息的相互比對(duì),來判斷該產(chǎn)品是否存在抄襲的行為。
2022-07-05 09:33:38 666
666 是隱藏的。無論哪種情況,您都可以利用示波器的統(tǒng)計(jì)分析。 考慮一個(gè)基本的示波器測(cè)量噪聲方波,如圖 1 所示。 ? 圖 1. 方波上的噪聲增加了尋找信號(hào)幅度的難度。 方波上的噪聲使得測(cè)量其幅度變得困難。幅度構(gòu)成其他測(cè)量的基礎(chǔ),
2022-07-21 16:29:00 3594
3594 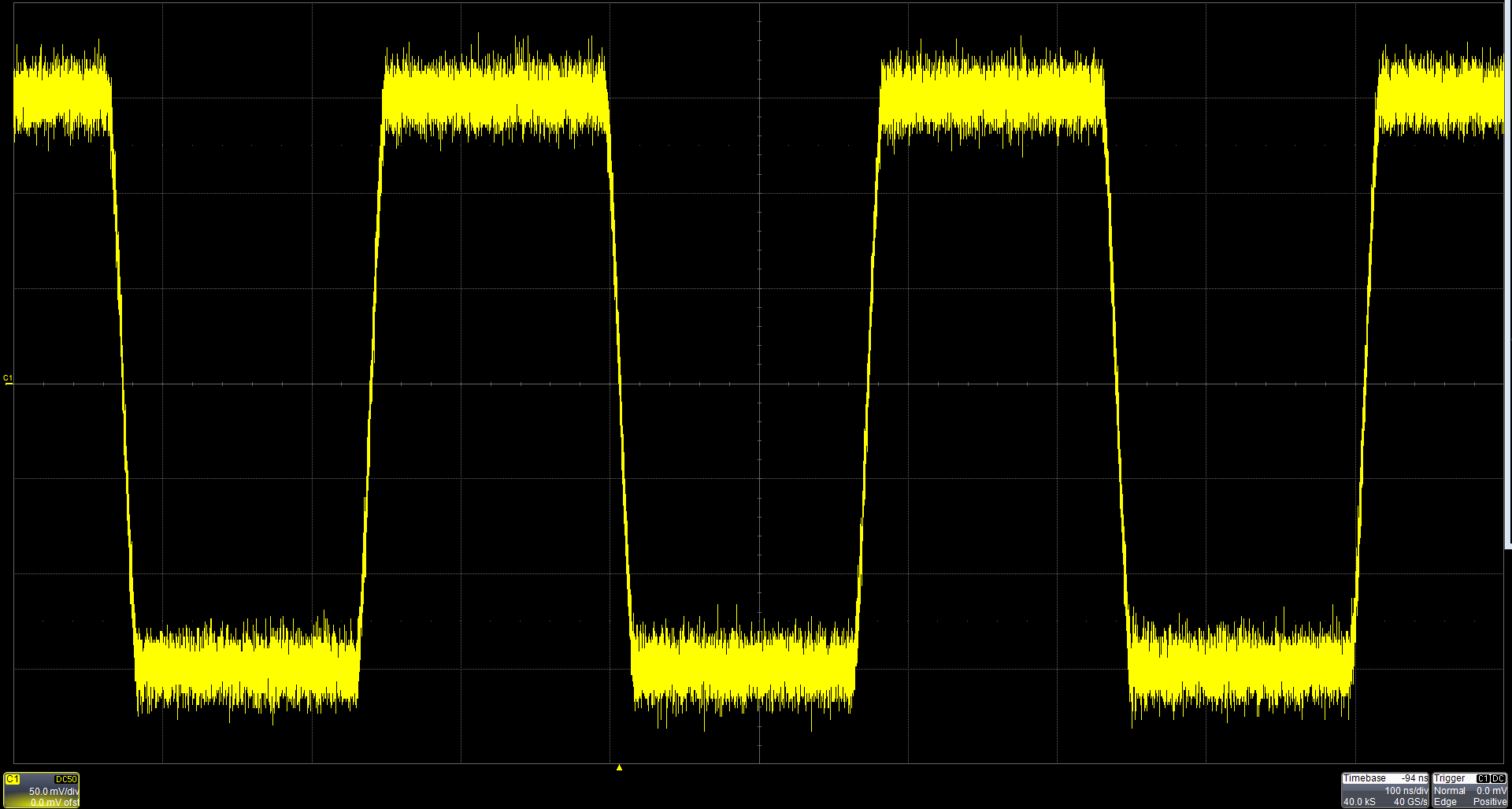
客流統(tǒng)計(jì)分析可以 1、精準(zhǔn)可靠的客流數(shù)據(jù)勝過萬千客戶的意見,管理者可直接通過客流數(shù)據(jù)來對(duì)當(dāng)前的在售商品及營(yíng)銷策略及時(shí)的做出科學(xué)有效的調(diào)整; 2、根據(jù)不同時(shí)段客流量的分布情況,使管理人員可以在客流高峰
2022-10-24 16:35:49 962
962 前面我們已經(jīng)講了PSpice提供的三種最基本的分析方法:直流分析、交流掃描分析和瞬態(tài)分析,也講了一種進(jìn)階分析:參數(shù)掃描分析,今天我們講一種統(tǒng)計(jì)分析方法——蒙特卡洛分析(Monte Carlo)
2022-11-10 09:57:20 10207
10207 言歸正傳,上一期昨天說到PSpice中的一種統(tǒng)計(jì)分析叫蒙特卡洛分析,它是用于呈現(xiàn)了電路中元器件的容差引起輸出結(jié)果偏離的統(tǒng)計(jì)結(jié)果。這時(shí)仿真中器件的容差是按照分布規(guī)律進(jìn)行選取,而樣本數(shù)越多結(jié)果越接近實(shí)際。
2022-11-11 09:46:47 2760
2760 stm32f722參考電路設(shè)計(jì)分析
2023-01-10 17:12:29 7
7 對(duì)于高速SerDes的仿真需要借助統(tǒng)計(jì)分析 (statistical analysis) 的方法。統(tǒng)計(jì)分析的方法把發(fā)送端-信道-接收端的連接近視為線性系統(tǒng),計(jì)算系統(tǒng)脈沖響應(yīng)h(t),加入噪聲源來模擬
2023-03-16 10:31:36 700
700 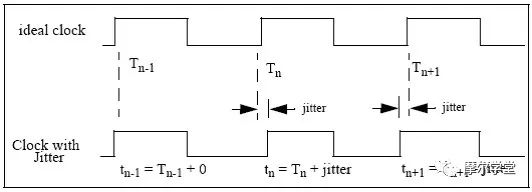
設(shè)備數(shù)據(jù)上云,解析后的設(shè)備數(shù)據(jù)一般是時(shí)序存儲(chǔ),但純粹的設(shè)備時(shí)序數(shù)據(jù)無法給用戶帶來更大的業(yè)務(wù)價(jià)值,需要根據(jù)業(yè)務(wù)需求進(jìn)行額外的數(shù)據(jù)統(tǒng)計(jì)分析。
2023-05-23 15:09:18 499
499 
相較于人臉識(shí)別攝像頭,毫米波客流統(tǒng)計(jì)雷達(dá)不會(huì)采集人臉圖像,有效保護(hù)個(gè)人隱私,規(guī)避隱私投訴風(fēng)險(xiǎn)。
2022-09-14 15:14:31 475
475 
智慧教室是當(dāng)今教育信息化的一大亮點(diǎn),通過物聯(lián)網(wǎng)技術(shù)和人工智能等多種技術(shù)手段,實(shí)現(xiàn)了信息化、智能化的課堂教學(xué)和管理。其中,數(shù)據(jù)統(tǒng)計(jì)分析功能是智慧教室建設(shè)的核心功用之一,為課堂教學(xué)評(píng)估提供重要依據(jù)
2023-05-19 09:40:46 305
305 
人員感知雷達(dá)WTR-812FAR保護(hù)隱私、功能完善、場(chǎng)景貼合度高,適用于商業(yè)綜合體、連鎖門店等多種客流統(tǒng)計(jì)分析場(chǎng)景,可對(duì)人員流動(dòng)數(shù)量、特征等進(jìn)行信息采集和輔助分析,幫助優(yōu)化經(jīng)營(yíng)策略、提升運(yùn)營(yíng)效率,為數(shù)智經(jīng)營(yíng)賦能。
2023-05-25 15:56:48 420
420 
進(jìn)行蒙托卡諾(Monte Carlo)統(tǒng)計(jì)分析,壞情況(Worst Case)分析、優(yōu)化設(shè)計(jì)等復(fù)雜的電路特性分析。
2023-08-02 14:20:15 542
542 
本文通過對(duì)我國(guó)24個(gè)省市453棟大型辦公建筑基本信息、運(yùn)行參數(shù)以及能耗數(shù)據(jù)進(jìn)行調(diào)研,分別對(duì)綜合能耗和電力消耗進(jìn)行了統(tǒng)計(jì)分析,在此基礎(chǔ)上分析了建筑固有特點(diǎn)以及運(yùn)行特點(diǎn)與能耗的相關(guān)性,得出我國(guó)
2023-11-27 10:02:07 179
179 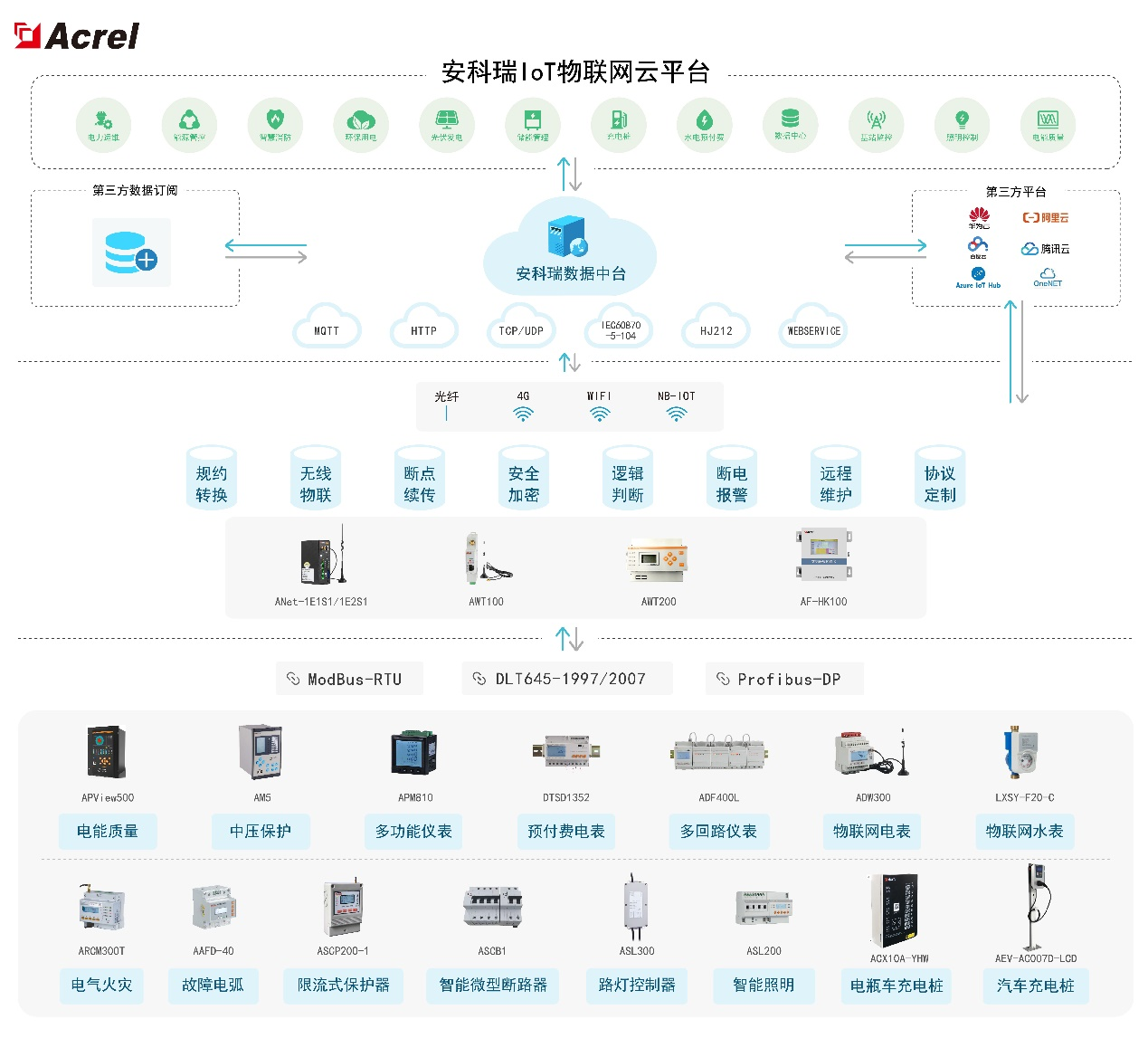
Arm Statistical Profiling Extension (SPE, 統(tǒng)計(jì)分析擴(kuò)展) 是一種架構(gòu)級(jí)功能,旨在增強(qiáng) Arm CPU 的指令執(zhí)行分析。
2024-01-24 18:16:42 690
690
正在加载...
 電子發(fā)燒友App
電子發(fā)燒友App






































評(píng)論