一個新的二進前向多層網學習算法及布爾函數優化實現
本文首先給出二進前向多層網幾何學習算法[1,2]的一個改進策略,提高了原算法的學習效率.然后提出一個新的神經網絡啟發式遺傳幾何學習算法(簡稱HGGL算法).HGGL算法采用面向知識的交叉算子和變異算子對幾何超平面進行優化的劃分,同時確定隱層神經元的個數及連接權系數和閾值.對任意布爾函數,HGGL算法可獲得迄今為止隱節點數最少的神經網絡結構.
關鍵詞:遺傳算法;神經網絡;學習算法;布爾函數
A New Learning Algorithm of Binary Neural Network Used for Optimum Design of Boolean Function
MA Xiao-min YANG Yi-xian
(Department of Information Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China)
ZHANG Zhao-zhi
(Institute of System Science,Academia Sinica,Beijing 100080,China)
Abstract:A modification to the geometrical learning algorithm of binary neural network,which tries to enhance efficiency of the algorithm,is demonstrated.Then a new Heuristic Genetic Geometrical Learning algorithm(called HGGL algorithm) of the neural network used for arbitrary Boolean function approximation is presented.The algorithm imtroduces knowledge based crossover operator and mutation operator to optimally divede geometrical hypercube and evaluate the number of the hidden neurons,connection weight and threshold. For arbitrary Boolean function,the neural network trained by HGGL algorithm has the fewest number of hidden layer neurons comparde with existed learning algorithms.
Key words:genetic algorithm;neural network;learning algorithm;Boolean function
一、引 言
布爾函數的簡化實現在編碼、密碼、數字邏輯設計等領域的理論和應用都有重要意義.設n元布爾函數f(X)=f(x1,x2,…,xn)為GF(2n)→GF(2)上的函數,其中GF(2n)為二元域GF(2)上的n維向量空間,xi∈{0,1},i=1,2,…,n.本文研究的核心是利用前向三層神經網絡實現或逼近任意布爾函數的輸入輸出映射.目前布爾函數神經網絡實現結構最簡單的是文[1,2]的幾何學習算法,把布爾函數輸入空間2n個二進制樣本視作n維超立方體的2n個頂點,隱層的學習是通過對學習樣本的幾何分析尋找一系列超平面對超立方體進行劃分,使得劃分后兩個超平面之間的學習樣本頂點擁有相同的布爾函數輸出,隱層網絡學習過程是劃分超平面的逐次產生過程,直至所有的樣本頂點都被相應的超平面分離.最后超平面的個數等于隱層神經元的個數,超平面方程的系數即為隱層神經元的權系數.幾何學習算法把非線性可分問題轉化為若干線性可分問題求解,從而用一個三層網實現任意布爾函數映射 .然而在幾何學習算法的訓練過程中,只有劃分超平面決定了全部布爾函數樣本頂點,學習才告結束.本文提出并證明了一個新的學習結束的判別條件,減少了可能的隱層神經元個數及學習時間.文[1,2]學習算法樣本的先后排序對學習效果影響很大,對于變量個數少的布爾函數可以利用窮舉法獲得最優的神經網絡實現結構,而對于變量個數多的布爾函數(如編碼密碼中的布爾函數),這種排序的搜索問題實際上是一個NP難解問題.在對幾何學習算法分析改進后,本文針對幾何學習提出一種啟發式遺傳算法,尋找最優的排序路徑,形成完整的HGGL學習算法.最后通過典型的例子說明了算法的特點及有效性.
二、幾何學習算法的改進策略
定義1 在學習過程中,已由超平面分離的線性可分樣本頂點稱為真頂點;其余樣本稱假頂點;確定超平面選擇的初始樣本頂點稱核心頂點.
定義2 設布爾函數數神經網絡學習樣本集合U={X1,X2,…,XN},其中N=2n,Xi={xi1,xi2,…,xin},則以某一個樣本為核心頂點的真頂點樣本集合稱為真頂點分離集VK={X1,X2,…,XK},其中K為集合中真頂點樣本的個數.XI為初始核心頂點.
神經網絡隱層的學習過程實質上是真頂點樣本集合VK擴展過程:在U-VK中隨機選擇樣本頂點Xk+1,滿足f(X,X∈Vk)=f(X,X∈Vk+1),并計算集合中心:(Ci/C0)=(1/(k+1))![]() 其中C0=k+1,x′i={0,1};i=1,2,…,n,對于Xj∈{Vk,Xk+1},,計算
其中C0=k+1,x′i={0,1};i=1,2,…,n,對于Xj∈{Vk,Xk+1},,計算![]() …,k+1;對于Xj∈U-{Vk,Xk+1},計算Tmin=minj
…,k+1;對于Xj∈U-{Vk,Xk+1},計算Tmin=minj![]() ,j=k+2,…,2n.這樣判別Xk+1是否可擴展為真頂點的條件為:
,j=k+2,…,2n.這樣判別Xk+1是否可擴展為真頂點的條件為:
Tmax<Tmin (1)
如果Xk+1可擴展,即Vk與U-Vk線性可分,Vk+1={Xk,Xk+1},得到權系數wi=2Ci-C0和閾值T=[(Tmax+Tmin)/2],[x]表示取整函數,否則尋找新的樣本頂點,不斷擴展直至U-Vk不再存在可擴展的與XK有相同布爾函數輸出的頂點樣本,則一個分離超平面形成,w1j={wi},Tj=T,這時有:當![]() ;當
;當![]() 0,從而確定一個隱層神經元,再令Vk的輸出取反,K=k,重復擴展.不斷得到新的超平面或隱層神經元,直至U-Vk=φ(所有樣本頂點訓練完畢).最后得到L個超平面及相應的神經網絡隱層結構.
0,從而確定一個隱層神經元,再令Vk的輸出取反,K=k,重復擴展.不斷得到新的超平面或隱層神經元,直至U-Vk=φ(所有樣本頂點訓練完畢).最后得到L個超平面及相應的神經網絡隱層結構.
輸出層的學習目的就是組合隱層神經元的輸出以產生理想的布爾函數輸出.輸出層的連接權系數及閾值w2j與θ按以下規則確定[1,2]:
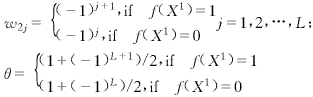 (2)
(2)
文[1,2]中在隱層的訓練中,僅當所有的學習樣本頂點都擴展為真頂點分離集合,學習才告結束.在確定超平面的過程中,下面定理將說明在某些情形下,這個學習結束條件是不必要的.這樣會減少若干分離超平面,意味著減少隱層神經元.
定理:在真頂點分離集合VK的擴展過程中,如果U-VK中所有樣本頂點布爾函數輸出相同,則只需要一個超平面(或一個隱層神經元)即可把這些樣本與VK中的其它樣本區分開來,并得到正確的布爾函數輸出.
證明:設分離集合VK中的K個樣本由L個超平面確定,根據真頂點分離集合的擴展原理可知:
![]()
而![]() j=K+1,…,2n,t=1,2,…,L
j=K+1,…,2n,t=1,2,…,L
故當樣本輸入屬于VK,至少有一個隱層神經元輸出為1,當樣本輸入不屬于VK,則隱層所有神經元輸出皆為0.因此若VK以外的樣本布爾函數值皆相同,超平面L就可以來區分這些樣本,不需再增加超平面,即使U-VK中有一些樣本不滿足式(1)真頂點的擴展條件,仍可得到正確輸出.證畢
上述定理為幾何學習算法學習結束提供了新的判別條件:即在真頂點分離集擴展過程中,當U=Vk中所有樣本布爾函數值相同時,則學習結束.
三、HGGL算法原理及其實現
前述幾何學習算法真頂點分離集擴展過程中,實現同一布爾函數初始核心頂點樣本的選擇及真頂點擴展的次序不同,需要,隱層神經元的個數差異很大.文[1,2]采用窮舉法,即每種可能的初始點及真頂點集合都試一遍,然后找到最優的一種組合和神經網絡結構.變量個數為n的布爾函數,其排列的可能性有(2n)!,因此對于變量很多的布爾函數很難在有限時間內實現.本文引入遺傳算法搜索樣本學習的最優排序即布爾函數實現復雜度最小的神經網絡結構.為避免加大樣本頂點超平面劃分的搜索空間,本文沒有采用基本的遺傳算子,而是基于知識采用了啟發式遺傳策略尋求此問題的最優解.
1.問題的編碼及遺傳群體的產生
把幾何學習算法中樣本真頂點分離集的擴展過程看作是樣本頂點在真頂點分離集中依次序排列的過程,遺傳算法的任務是尋找一組或若干組最優真頂點樣本的排列,使得神經網絡實現布爾函數所需隱層神經元個數最少.遺傳算法的每個基因串按如下方式編碼:P={p1,p2,…,p2n},pi∈{1,2,…,2n},i=1,2,…,2n
首先把學習樣本從1~2n按次序逐個編號表示樣本在基因串中的順序位置,即P表示真頂點分離集中各樣本參與學習的先后順序,代表序號為pi的樣本在時刻i擴展參與學習.根據啟發式遺傳算法的要求,P中所代表樣本頂點必須為合法真頂點,所謂合法真頂點應滿足如下判別條件:設Vi-1={Xp1,Xp2,…,Xpi-1}對任意pi代表的新樣本Xpi,①與P中已有樣本點序號沒有重復;②滿足式(1)真頂點分離集擴展條件.
在遺傳算法中,對每一個基因串都有一個衡量其特性的適合度函數作如下定義:
fa(P)=1/L (3)
這里L表示P排列下,幾何劃分的超平面個數或神經網絡所需神經元的個數,超平面個數越少,則P的適合度函數越大,適合度大的基因串繁殖下一代的概率也大.
2.遺傳算子的設計
遺傳算子通過交叉、變異、選擇三個遺傳算子以產生下一代更優秀性能的群體.
交叉是指把父代基因串的部分結構加以替換重組而生成新個體的操作,通過交叉子代個體繼承了父代個體遺傳特性,交叉是HGGL算法尋找最優解的主要手段,由于基于神經網絡學習的幾何超平面劃分問題采用的是樣本序號的編碼,若采取簡單的一點交叉或多點交叉策略,必然以極大的概率產生非法的真頂點分離集合.因此本文引入了基于知識的交叉方法,對于父代基因串P={p1,p2,…,p2n},交叉算子構造后代:Q={q1,q2,…,q2n},qi∈{1,2,…,2n},i=1,2,…,2n,以概率Pc從上一代群體中選取適合度較大的基因串進行交叉:
①隨機選取一個樣本頂點,并把其序號作為初始核心樣本序號q1.集合V1={Xq1};
②For K=1 to 2n-1.給定Vk={Xq1,…,Xqk},在父代個體P中尋找與qk鄰接的序號,設為pm.并根據式(1)判別Xpm是否為合法真頂點集合,如果是,則令qk+1=pm;如果不是,則在U-Vk中尋找新的合法真頂點添加到真頂點集合,尋找途徑為:首先尋找與qk輸出相同的樣本頂點;如果找不到合法點則找與qk輸出相異的頂點;
③重復②相類似的操作,不斷繼承父代基因串的相鄰樣本序號,或尋找新的合法樣本得到q3,q4,…,直至構造出完整的子代基因串Q.如果某一時刻i,U-Vk的樣本滿足定理1的條件,交叉提前完成,qi,qi+1,…,q2n可隨意排列.
變異算子是對群體中的個體串的某些基因座上的基因值作變動,以幫助遺傳算法的交叉算子擺脫在進化過程中使得群體陷于搜索空間中某個超平面的局面.從而加速向全局最優解收斂.考慮到一般的變異策略也會產生非法的真頂點分離集合,引入基于知識的變異方法如下:
①以很小的變異概率Pm,在上一代群體中隨機選取父代基因串中輸出相同的兩個樣本序號,交換其位置;
②判別被操作的基因串是否為合法真頂點分離集合,如果是則變異結束;
③否則,以擴展過程中第一個不合法樣本點為起點,依據前述的交叉方法,構造新的合法后代基因串.選擇即是把上一代群體中的個體按一定規律選中繁衍下一代.HGGL的選擇策略為:
①計算上一代每一個個體的適合度函數fa;②以選擇概率Ps比例產生適合度函數值較大的個體作為下一代群體中的個體.
四、HGGL算法實現流程及計算機仿真結果
給定任意布爾函數學習樣本及其相應的輸出,HGGL創建一個復雜性最低的三層前向神經網絡,完全實現布爾函數的輸入輸出映射關系.HGGL算法的主要流程可歸納如下:
①初始化 根據具體任務,確定遺傳算法的交叉概率Pc(0.6~0.9),變異概率Pm(0.01~0.15),選擇概率Ps(0.8~0.95),確定群體大小N,一般取20~60,給定布爾函數變量個數n,樣本個數M=2n.
②問題編碼 第一代群體的產生,以幾何學習算法確定隱層神經元連接系數及閾值集合,產生N個個體,并計算每個個體的適合度.
③下一代群體的進化 對上一代群體中的個體進行交叉、變異、選擇等遺傳操作,保留適應值最大的個體直接進入下一代群體,產生下一代N個個代,并計算每個個體的適合度及超平面方程的系數集合.
④重復②③直至滿足下面的收斂條件 a.進化的代數等于預先給定的Gmax代群體;b.同一代群體中所有基因串的適合度函數幾乎相等.
⑤選擇最優的個體作為隱層學習的最終結果 隱層神經結構已經確定.
⑥輸出層的學習 根據式(2)輸出層學習方法,確定輸出層的權系數及閾值.
本文通過C語言仿真實現了HGGL算法,對許多布爾函數進行學習,得到了一系列很好的結果,下面給出其中一個典型例子.
例 5位布爾函數的實現[1],其布爾函數輸出可表示為:
f(0~31)=(0,0,1,0,1,1,0,1,1,1,1,1,0,1,1,0,1,0,0,0,1,0,0,1,0,0,1,0,1,0,0,0)
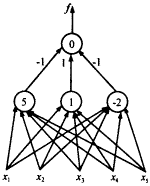
取輸入個數n=5,超立方體頂點個數為32,交叉概率Pc=0.8,變異概率Pm=0.01;選擇概率Ps=0.9,遺傳算法群體個數N=30,每個串基因的長度為32.HGGL經20代的遺傳學習,獲得的最優排序其相應的超平面參數(即隱層神經元的權系數及閾值)如表1所示,布爾函數只需要3個隱層神經元.由式(2)確定輸出層神經元連接權系數,實現此布爾函數的三層神經網絡如圖1所示,經實驗驗證:HGGL算法能夠可靠收斂,如果沒有變異,算法在很多情形下收斂不到最優值,而沒有每代最優基因串的直接繼承,收斂曲線會出現振蕩,收斂得不到保證.同樣的布爾函數文[4]需要15個隱層神經元,文[3]需要至少8個神經元,而文[1]的幾何學習算法經窮舉得到的優化結果為4個隱層神經元.由于本文采用新的學習判別準則和遺傳算法尋優,得到了目前最好的實現結果.
表1 最優排序結果及超平面系數
| 輸入樣本序號 | 隱層神經元的權系數與閾值 | |||||
| m=(x1x2x3x4x5)10 | wi1 | wi2 | wi3 | wi4 | wi5 | T |
| 21,17,1,19,25,29 | 4 | -2 | -2 | -4 | 6 | 5 |
| 16,20,23,5,9,13,4,7,28 | 3 | -5 | 3 | -9 | 7 | 1 |
| 0,3,31,12,15,6,22,18,24,27,30 | 4 | -4 | 4 | -4 | 4 | -2 |
| 26,2,8,11,10,14 | ||||||
|
圖1 5位布爾函數實現網絡 五、結 論 |
 電子發燒友App
電子發燒友App










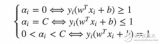













評論