時變時延的在線自適應估計
本文提出了一種時變時延的在線自適應估計新方法.首先,本文給出了一種修正的強跟蹤濾波器算法,并且建立了時變時延的估計模型.基于此模型,時變時延可以被當成系統狀態由修正的強跟蹤濾波器算法直接進行估計.所提出的方法具有使用簡單、跟蹤迅速、精度高等特點.最后,仿真實驗結果驗證了本文方法的有效性.
關鍵詞:時變;時延;自適應估計;在線
On-Line Adaptive Estimation of Time-Varying Time Delay
ZHOU Dong-hua
(Dept.of Automation,Tsinghua University,Beijing 100084,China)
Abstract:A new approach to on-line adaptive estimation of time-varying time delay is proposed.First,a modified strong tracking filter algorithm is presented,and an estimation model for the time-varying time delay is set up.Based on this model,the time-varying time delay can be directly estimated by the modified strong tracking filter algorithm.The proposed approach is characterized by easy implementation,rapid tracking,high accuracy and etc.Finally,simulated experimental results are provided to show the effectiveness of the proposed approach.
Key words:time-varying;time delay;adaptive estimation;on-line
一、引 言
不同地點的兩個傳感器所接收的同一信號一般都存在時延,這個時延的估計與跟蹤技術在諸如聲納、雷達等對象的信號處理中具有重要的作用.設y1(k+1),y2(k+1)是兩個傳感器上得到的觀測序列,即:
![]() (1)
(1)
其中,s(k+1)是源信號,e1(k+1),e2(k+1)是零均值、獨立的白噪聲,其方差分別為R1和R2,a是已知的信號衰減因子.T(k+1)是兩感器之間的時變時延,其值是未知的非負整數.現在的研究目標就是要給出T(k+1)的有效估計方法.
此問題近年來已受到了國內外學者的關注.文獻[1]采用高階統計量方法,給出了一種有效的定常時延的估計方法.文獻[2]基于梯度算法給出了一種時變時延的估計方法,其前提條件是誤差函數必需是單峰的.利用隨機逼近算法,文獻[3]得到了一種時變時延的估計方法,其缺點是動態跟蹤精度太差.文獻[4]和文獻[5]給出了兩種有效的時變時延的估計方法,然而,它們具有算法復雜,設計困難的共同缺點.
本文基于一種修正的強跟蹤濾波器算法,給出一種新的時變時延的在線自適應估計方法.所提出的方法具有使用簡單,跟蹤迅速,精度高等特點.仿真實驗結果驗證了本文方法的有效性.
二、一種修正的強跟蹤濾波器算法
一類離散時間非線性系統由下式描述:
![]() (2)
(2)
其中狀態x∈Rn,輸入u∈Rp,輸出y∈Rm,非線性函數f:Rm×Rn→Rn和h:Rn→Rm對x有連續的偏導數;過程噪聲v(k)∈Rq是零均值,方差為Q(k)的高斯白噪聲,測量噪聲e(k)∈Rm也是零均值,方差為R(k)的高斯白噪聲,Γ(k)是已知的適當維數的矩陣,v(k)和e(k)是統計獨立的.
通過引入一個弱化因子β,我們在這里進一步給出關于系統I的一種修正的強跟蹤濾波器(MSTF-Modified Strong Tracking Filter),由下式給出:
(k+1|k+1)=(k+1|k)+K(k+1)γ(k+1) (3)
(k+1|k)=f(k,u(k),(k|k)) (4)
其中,
K(k+1)=P(k+1||k)HT(k+1,(k+1|k))[H(k+1,
(k+1|k))P(k+1|k)HT(k+1,(k+1|k))
+R(k)]-1 (5)
P(k+1|k)=LMD(k+1)F(k,u(k),(k|k))P(k|k)
FT(k,u(k),(k|k))+Γ(k)Q(k)ΓT(k) (6)
P(k+1|k+1)=[I-K(k+1)H(k+1,(k+1|k))]P(k+1|k) (7)
γ(k+1)=y(k+1)-h(k+1,(k+1|k)) (8)
其中,![]() (9)
(9)
![]() (10)
(10)
LMD(k+1)=diag{λ1(k+1),λ2(k+1),…,λn(k+1)} (11)![]() (12)
(12)
![]() (13)
(13)
N(k+1)=V0(k+1)-β.R(k+1)-H(k+1,(k+1|k))
.Γ(k)Q(k)ΓT(k)HT(k+1,(k+1|k)) (14)
M(k+1)=F(k,u(k),(k|k))P(k|k)FT(k,u(k),
(k|k))HT(k+1,(k+1|k))H
.(k+1,(k+1|k))=(Mij) (15)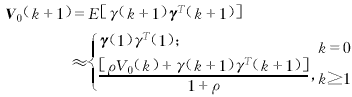 (16)
(16)
其中ρ=0.95是遺忘因子,β![]() 1是一預先選定的弱化因子.選取原則為αi
1是一預先選定的弱化因子.選取原則為αi![]() 1,i=1,2,…,n[6].下面給出弱化因子的物理意義.
1,i=1,2,…,n[6].下面給出弱化因子的物理意義.
由求取漸消因子的公式(11)~(16)得知,只有當:
V0(k+1)-β.R(k+1)-H(k+1,(k+1|k))Γ(k)Q(k)ΓT(k)HT(k)HT(k+1,(k+1|k))>0時,漸消因子才有可能起作用.由于已知R(k+1)>0,因此,選擇更大的弱化因子β將減弱漸消因子的調節作用,使得估計值更加平滑.但是,若選擇的β值太大,漸消因子將永不會起作用,此MSTF就會退化為通常的擴展卡爾曼濾波器(EKF),濾波效果反而會變差.怎樣選取一個最優的β是一個有待解決的問題.實際應用時,可以通過計算機仿真,根據估計的總體誤差,很容易地選擇一個適當的β.
此MSTF的計算量與STF的計算量幾乎完全一樣[8].因此,此MSTF算法是一種實時算法.
三、時變時延的估計方法
首先,給出如下定義:
定義1:實數b的整數部分記為INT(b).
定義2:實數b的偏上整數記為round(b),由下式定義:
![]() (17)
(17)
為估計時延T(k+1),我們建立如下估計模型:
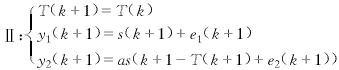 (18)
(18)
將式(18)與式(2)相比較,當把T(k)看做狀態變量x(k),[y1(k+1) y2(k+1)]T作為輸出變量時,上節給出的修正的STF算法可以直接用來估計T(k).此時有:
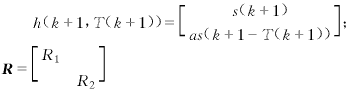
考慮到估計出的時延應該為非負整數,由定義1和2,為方便起見,分別把時延的估計值![]() (k|k)和預報值
(k|k)和預報值![]() (K+1|k)的偏上整數記做
(K+1|k)的偏上整數記做![]() (k|k)和
(k|k)和![]() (k+1|k),即,
(k+1|k),即,![]() (k|k)=round(
(k|k)=round(![]() (k|k)),
(k|k)),![]() (k+1|k)=round(
(k+1|k)=round(![]() (k+1|k)).此時,應該用下面兩公式替代原公式(9)和(10).
(k+1|k)).此時,應該用下面兩公式替代原公式(9)和(10).
![]() (19)
(19)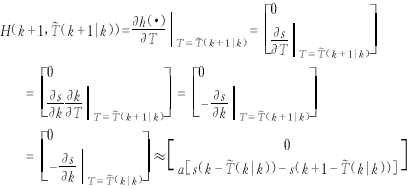 (20)
(20)
式(20)中,用到了恒等式![]() (k+1|k)=
(k+1|k)=![]() (k|k),此式來自
(k|k),此式來自![]() (k+1|k)=
(k+1|k)=![]() (k|k).這是由式(18)中的第1式和式(4)得到的.
(k|k).這是由式(18)中的第1式和式(4)得到的.
另外,式(8)中的![]() (k+1|k)也應由
(k+1|k)也應由![]() (k|k)替代.顯然,這時的修正STF算法中,Γ(k)=1,u(k)=0,Q=0,αi=1.
(k|k)替代.顯然,這時的修正STF算法中,Γ(k)=1,u(k)=0,Q=0,αi=1.
由式(13)得知,Mii不能全部為零,因此由式(15)得知,H(.)永遠不能為零矩陣.為此,可以把式(20)修改為:
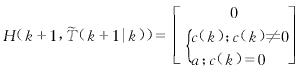 (21)
(21)
其中,c(k)=a[s(k-![]() (k|k))-s(k+1-
(k|k))-s(k+1-![]() (k|k))].
(k|k))].
四、仿真實驗
實驗1:
源信號s(k)是周期為16,幅度為±1的方波,a=0.4,噪聲信號的協方差矩陣為R0=diag[0.022 0.022],時變時延設置成:
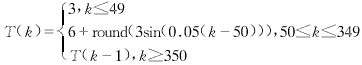
在修理正的STF算法中,取![]() (0|0)=1≠T(0),β=5,P(0|0)=100,R=R0.仿真實驗結果由圖1所示.
(0|0)=1≠T(0),β=5,P(0|0)=100,R=R0.仿真實驗結果由圖1所示.
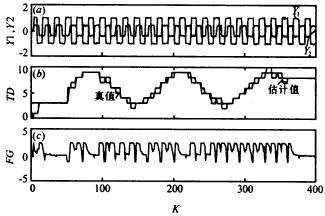
|
圖1 例1仿真實驗結果;TD:時滯;FG:濾波器增益 實驗2: |
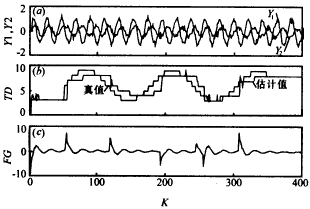
|
圖2 例2仿真實驗結果;TD:時滯;FG:濾波器增益 實驗3: |
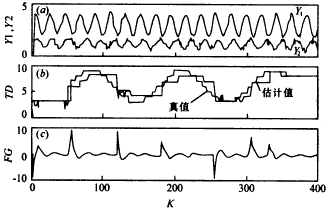
|
圖3 例3仿真實驗結果;TD:時滯;FG:濾波器增益 上述實驗結果驗證了如下結論: 五、與其它方法的比較 六、結 論 |
 電子發燒友App
電子發燒友App




















評論