基于最大峰度準則的非因果AR系統盲辨識
本文結合最大峰度準則和非線性優化理論中的梯度法,設計了一種非因果AR系統的盲辨識算法,并證明了它的全局收斂性,給出了它在平衡點附近的收斂速度.算法通過構造逆濾波器的方法來進行盲辨識,同時通過基于高階累積量的自學習算法將逆濾波器的系數逼近AR系統的參數.由于采用了高階累積量,算法對高斯觀測噪聲有較好的抑制能力.仿真的結果表明了算法的有效性.
關鍵詞:非因果系統;盲辨識;高階累積量;最大峰度準則
Blind Identification of Noncausual AR System Based on Maximum Kurtosis Criteria
ZHAO Xi-kai,ZHANG Xian-da
(Dept.of Automation,Tsinghua University,Beijing 100084,China)
Abstract:Based on the maximum kurtosis criteria and gradient decent method,this paper designed a new blind identification algorithm for noncausual AR system.Its global convergence is proved and convergence rate calculated.Parameters in the inverse filter approach the true AR coefficients by high-order cumulant (HOS) based self-study algorithm.This identification method can effectively suppress the Gaussian noise because of the utilization of HOS.
Key words:noncausual system;blind identification;higher-order culmulant;maximum kurtosis criteria
一、引 言
在地震勘探、通訊和水聲信號處理等許多領域,經常需要辨識非因果系統.要解決這類非因果系統的盲辨識問題、單靠相關函數是不夠的,因為它不包含系統的相位信息[1].
基于高階統計量的系統辨識方法在近年來受到了高度的重視.同基于相關函數的傳統辨識方法相比較,高階統計量的優點在于:1.可保留系統的相位信息,從而有效地辨識非最小相位、非因果系統.2.可以抑制加性有色噪聲的影響,提高算法的魯棒性.在各種高階統計量中,四階統計量由于計算相對簡單,可以處理對稱分布信號而受到人們的特別重視,成為許多算法的基礎.
在文獻[3]的基礎上,本文提出了最大峰度準則,并將其應用到非因果系統的辨識中.通過非線性優化中的梯度法,本文設計了一種AR系統的盲辨識算法,并證明了它的全局收斂性,給出了算法在平衡點附近的收斂速度.算法通過構造逆濾波器的方法來進行盲辨識,同時通過基于高階累積量的自學習算法用逆濾波器的系數逼近AR系統的參數.這個算法可以辯識非因果系統并且也可用于反卷積或者盲均衡.由于采用了高階累積量,算法對高斯觀測噪聲有較好的魯棒性.
二、基于最大峰度準則的系統辨識算法
設有一未知的線性時不變系統H,其輸入序列{u(n)}也未知,我們只觀測到其輸出序列{x(n)},n=0,1,…,N-1,其中N為測量序列的長度.系統模型為
x(n)=u(n)*h(n)+w(n) (1)
其中{w(n)}是量測噪聲.h(n)是未知的線性時不變系統H的單位脈沖響應.
對這個模型中的信號特性做如下假設:
(A1)線性時不變系統H是穩定的,但它不一定是最小相位,也不一定是因果的,它存在一個穩定的逆系統H-1.
(A2){u(n)}是平穩的零均值非高斯實信號,而且是一個獨立同分布信號,它的m階累積量γm存在,m![]() 3.加性噪聲{w(n)}服從高斯分布,其統計特性未知,且與輸入信號{u(n)}相獨立.
3.加性噪聲{w(n)}服從高斯分布,其統計特性未知,且與輸入信號{u(n)}相獨立.
設對逆系統H-1的估計為V,則V的輸出{y(n)}為
y(n)=x(n)*v(n)=u(n)*g(n)+w′(n) (2)
其中w′(n)=w(n)*v(n)仍為一高斯噪聲,g(n)是由下式給出的穩定的濾波器
g(n)=h(n)*v(n) (3)
與通常的峰度定義不同,定義信號x(t)的(規范化的)峰度K42x為
K42x=c4x(0,0,0)/[c2x(0)]2=γ4x/[σ2x]2 (4)
為了克服Shalvi & Weinstein提出的準則[2]中要求信號的方差相等的限制,可以把式(4)定義的(規范化)的峰度值做為準則函數,這使它更適合于實際應用環境定義的準則函數為
J(v(n))=|K42y|=|γ4y/(σ2y)2| (5)
需要說明的是,這個準則函數實際上是Chi & Wu[3]提出的一大類準則函數中的一個特例.他們提出的準則函數為:
Jl+s,2s(v(n))=|γl+s,y|2s/|γ2s,y|l+s (6)
其中l>s![]() 1.
1.
顯然,式(5)是式(6)在l=3,s=1時的特例.該準則函數的有效性在[3]中得到了證明,但本文將證明基于式(5)這個準則的算法的全局收斂性和收斂速度.
對于非因果AR系統,其逆濾波器是一個因果MA系統和一個反因果MA系統的極聯,設這兩個系統分別為ω(i)和![]() (i).針對上面的準則函數,可以利用非線性優化中的梯度法,得到ω(i)和
(i).針對上面的準則函數,可以利用非線性優化中的梯度法,得到ω(i)和![]() (i)的自學習算法為:
(i)的自學習算法為:
![]() (7)
(7)![]() (8)
(8)
式中的數學期望在實際應用中都由相應的均值估計代替.當K42x為正時,x(t)為所謂超值,保證K42y不斷向正的方向增大;當K42x為負時,x(t)為亞高斯(Sub-Gaussian)信號,α取負值,K42y不斷減小,|K42y|增大.
三、算法的全局收斂性
因為本文采是非線性優化方法,這就必然涉及到一個問題:算法收斂到的是全局極值點還是局部極值點?下面的定理表明算法必然收斂到全局極值點.
定理:式(7),式(8)的算法的收斂點是全局極值點.
證明:根據輸入和輸出之間高階累積量的關系,可以把準則函數改寫為
J(v(n))=|K42u|∑g4(n)/[∑g2(n)]2 (9)
去掉其中與輸入有關的常數,可以把目標函數進一步簡化為
J(g(n))=∑g4(n)/[∑g2(n)]2 (10)
由式(10),得到下列駐點方程
![]()
j=1,2,… (11)
由式(11),駐點為g(j)=0或g2(j)=c,其中c=∑g4(i)/∑g2(i)為一常數.為了便于敘述,定義由駐點gM(j)組成的集合GM,M=1,2,…,即
GM={gM:gM(j)符合式(11),且gM中有M個非零元素} (12)
由文獻[3]關于準則有效性的證明,知道G1是由所有全局極值點組成的集合,下面證明GM,M![]() 2是由不穩定平衡點(鞍點)組成的集合,即利用本算法不會收斂到局部極值點.
2是由不穩定平衡點(鞍點)組成的集合,即利用本算法不會收斂到局部極值點.
假定![]() ∈GM為
∈GM為
![]() (13)
(13)
其中IM=(k1,…,KM)是一個有M個不重復正整數的集合.構造一個向量![]() .
.
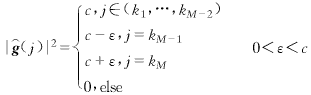 (14)
(14)
它的準則函數為
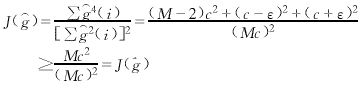 (15)
(15)
只要ε>0,上面的不等式就嚴格成立.也就是說,在![]() 的任何小的領域里,總存在
的任何小的領域里,總存在![]() 使得J(
使得J(![]() )>J(
)>J(![]() ),所以
),所以![]() ∈GM不可能是局部極大值.下面證明它也不是局部極小值.
∈GM不可能是局部極大值.下面證明它也不是局部極小值.
設kM+1![]() IM,構造如下的一個向量g)
IM,構造如下的一個向量g)
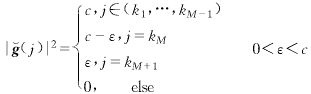 (16)
(16)
它的準則函數為
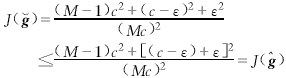 (17)
(17)
因為c>ε>0,上面的不等式嚴格成立,所以![]() ∈GM不可能是局部極小值.
∈GM不可能是局部極小值.
綜上所述,![]() ∈GM,M
∈GM,M![]() 2是準則函數的不穩定平衡點.因此按照式(7),式(8)的梯度尋優算法收斂到的必然是全局極值點.證畢.
2是準則函數的不穩定平衡點.因此按照式(7),式(8)的梯度尋優算法收斂到的必然是全局極值點.證畢.
上述定理表明,本算法對任何初始值都不會收斂到不希望的局部極值點,這無疑是一個非常可貴的性質.本文例2的仿真結果說明了這一性質.
四、算法的收斂速度
下面考慮算法的收斂速度.不失一般性,假設平衡點為![]() (i)=δ(τ),g(i)為偏離平衡點的一個迭代值.
(i)=δ(τ),g(i)為偏離平衡點的一個迭代值.
![]() (18)
(18)
定義![]() 則有,
則有,
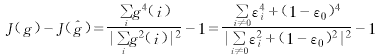
≈(1-4ε0)/|1+ε-2ε0|2-1(推導中去掉了分子中ε,ε0所有的二次以上項)
≈(1-4ε0)|1-ε+2ε0|2-1
≈-2ε(推導中去掉了ε,ε0所有的二次以上項) (19)
由式(18)和(19),得到
J(g)-J(![]() )∝‖g-
)∝‖g-![]() ‖2 (20)
‖2 (20)
可見在全局極值點附近,準則函數是以平方速度變化的.因此本文提出的基于梯度法尋優的學習算法在平衡點附近將線性收斂.從下節例1的圖1和圖2中可以看到在接近收斂點附近,辨識的各個參數都以幾乎相同的斜率收斂到終值.
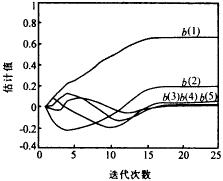
圖1 反因果部分辨識過程
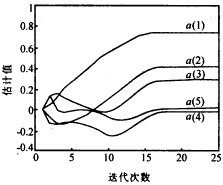
圖2 因果部分辨識過程
五、仿真結果
此處給出兩種典型情況的仿真結果,在所有仿真中加性觀測噪聲為高斯白噪聲,輸入信號是指數分布的隨機過程(均值為零,λ=1),數據長度為3000.學習常數開始時為0.5,在學習過程中逐漸減小為0.1.對每個例子均為30次Monte Carlo實驗.
例1.(非因果系統的辨識)真實AR模型為![]()
它的極點位于-0.0506±j0.6532,-0.6988,和-1.7500±h1.3919,信噪比SNR=10dB辨識時取m=5和n=5,即因果MA部分和反因果MA部分分別比實際模型高兩階和三階.辨識結果見表1和表2.
表1 非因果AR系統的因果部分辨識結果
| a(1) | a(2) | a(3) | a(4) | a(5) | |
| 真實值 | 0.8 | 0.5 | 0.2 | 0 | 0 |
| 均值 | 0.7700 | 0.4524 | 0.2375 | -0.0296 | -0.0041 |
| 標準差 | 0.0654 | 0.0759 | 0.0741 | 0.0492 | 0.0322 |
|
表2 非因果AR系統的反因果部分辨識結果 |
| b(1) | b(2) | b(3) | b(4) | b(5) | |
| 真實值 | 0.7 | 0.2 | 0 | 0 | 0 |
| 均值 | 0.6738 | 0.2015 | 0.0261 | 0.0215 | 0.0019 |
| 標準差 | 0.0812 | 0.0677 | 0.0485 | 0.0419 | 0.0337 |
| 圖2和圖3為最后一次Monte Carlo實驗中b(i)和a(i)估計值的變化過程.由圖中可以看到,在經過大約18次學習后,AR參數的估計值就收斂到真實值. |
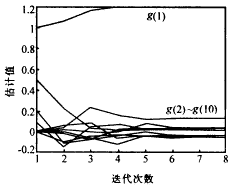
|
圖3 g(i)的變化過程 例2 (反卷積:回響消除)假設房間的回響效果可以用以下的3階MA模型表示,它的參數為h(0)=l,h(l)=0.5,h(2)=0.2,h(3)=0.1.為了減小截斷效應,仿真時取反卷積濾波器的階數為m=10.設g(i)=h(i)*a(i). 表3 g(i)的終值 |
| g(1) | g(2) | g(3) | g(4) | g(5) | g(6) | g(7) | g(8) | g(9) | g(10) | |
| 終值 | 1.196 | 0.023 | 0.027 | 0.016 | 0.137 | -0.01 | -0.04 | -0.03 | -0.04 | -0.05 |
| 終值 | -0.01 | -0.02 | 0.001 | 0.057 | 1.296 | 0.023 | 0.025 | 0.023 | 0.151 | -0.02 |
| 六、結 論 在文獻[3]的基礎上,本文提出了基于二階和四階統計量的最大(規范化)峰度準則,并設計了基于這種準則的非因果AR系統辯識算法,這個算法同時也可以用于盲反卷積或盲均衡中.與文獻[3]未對算法作性能分析不同,本文證明了算法不但是全局收斂的,而且在平衡點附近將以線性速度進行收斂.仿真的結果驗證了我們的結論. |
 電子發燒友App
電子發燒友App
























評論