????? 實(shí)時(shí)數(shù)字信號(hào)處理、超大規(guī)模集成電路技術(shù)的飛速發(fā)展,不斷地推動(dòng)著數(shù)字信號(hào)處理器性能的提高,使其在信號(hào)處理、軍事及民用電子技術(shù)領(lǐng)域發(fā)揮著越來越重要的作用,其應(yīng)用廣度和深度也在不斷地?cái)U(kuò)展和深化。數(shù)字信號(hào)處理相對(duì)于模擬信號(hào)處理有很大的優(yōu)越性,主要表現(xiàn)在精度高、靈活性強(qiáng)、可靠性好、易于大規(guī)模集成及存儲(chǔ)等方面,而且可以采用多種性能優(yōu)良的數(shù)字信號(hào)處理方法和算法。實(shí)時(shí)數(shù)字信號(hào)處理技術(shù)的核心和標(biāo)志是數(shù)字信號(hào)處理器。快速傅里葉變換等實(shí)用算法的提出,促進(jìn)了實(shí)現(xiàn)數(shù)字信號(hào)處理的發(fā)展。數(shù)字信號(hào)處理在于運(yùn)算處理的實(shí)時(shí)性。
?????? 電能表作為電能的計(jì)量工具,多年來一直倍受國家電力部門的重視,電能表生產(chǎn)企業(yè)更是不遺余力地致力于設(shè)計(jì)與開發(fā),但目前我國電能表設(shè)計(jì)水平仍比較落后,高精度電能表主要依靠進(jìn)口,傳統(tǒng)的4位、8位單片機(jī)因?yàn)樽陨硇阅艿木窒蓿诟呔?a target="_blank">電能計(jì)量方面難免捉襟見肘,而DSP技術(shù)在電能表中的應(yīng)用為電能計(jì)量精度的大幅度提高帶來了新的希望。
? &nbs?
p;??? DSP在電能表中的應(yīng)用
?????? 根據(jù)電能表的功能和誤差精度的需求,我們選用了TI公司的TMS320VC5402芯片,在程序設(shè)計(jì)上除了完成快速數(shù)據(jù)處理工作以外,還針對(duì)系統(tǒng)非線性失真進(jìn)行了修正和補(bǔ)償。
?????? 采集數(shù)據(jù)處理與計(jì)算
?????? 在實(shí)際應(yīng)用中,電力信號(hào)通過互感器采集到電能表中,通過一個(gè)6通道16位模擬輸入前端處理器(AD73360)進(jìn)行(A/D)模數(shù)轉(zhuǎn)換,變成數(shù)字信號(hào)并傳輸?shù)紻SP中,然后對(duì)采樣的數(shù)據(jù)進(jìn)行數(shù)字濾波。在DSP中應(yīng)用采樣技術(shù)需要快速ADC,即以非常快的速度來采樣模擬信號(hào),并且需要快速DSP來執(zhí)行數(shù)字低通濾波和抽取。在數(shù)字信號(hào)處理中,濾波占極其重要的作用,它解決了模擬濾波器無法克服的電壓漂移、溫度漂移和噪聲等問題,從而改善了數(shù)字信號(hào)的跳動(dòng),使得電壓電流信號(hào)的波形趨于理想狀態(tài)。電能表原理框圖示于圖1。
?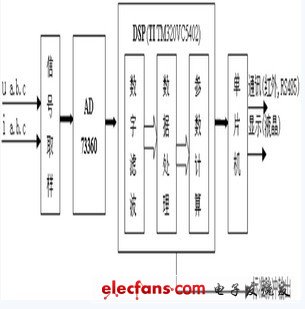
圖 1?? 電能表的原理框圖
?????? 在采樣過程中,首要的問題是采樣頻率的選擇,Nyquist采樣定理指出:若連續(xù)信號(hào)x(t)是有限帶寬的,其頻譜的最高頻率為fc,對(duì)x(t)采樣時(shí),若保證采樣頻率fs≥2fc,那么,就可由采樣信號(hào)恢復(fù)出x(t)。在實(shí)際對(duì)x(t)作采樣時(shí),首先要了解x(t)的最高截止頻率fc,以確定應(yīng)選取的采樣頻率fs。若x(t)不是有限帶寬的,在采樣前應(yīng)使用抗混疊(anti-aliasing)濾波器對(duì)x(t)作模擬濾波,以去掉f>fc的高頻成分。因此,在A/D轉(zhuǎn)換前就需要模擬低通濾波器具有尖銳的滾降特性,來限制模擬信號(hào)的頻譜。一個(gè)理想的濾波器應(yīng)能讓所有低于fs/2的頻率通過,而完全阻隔掉所有大于fs/2的頻率。通常,濾波器和采樣頻率的選擇是將我們感興趣的頻帶限制在DC和fs/2之間。
?????? 首先對(duì)電壓電流輸入信號(hào)進(jìn)行數(shù)據(jù)采樣和RC濾波網(wǎng)絡(luò)濾波,然后進(jìn)行A/D轉(zhuǎn)換。A/D轉(zhuǎn)換完成后產(chǎn)生中斷,在中斷服務(wù)子程序中讀出每次轉(zhuǎn)換的結(jié)果,作為數(shù)字低通濾波的輸入。DSP的輸入是A/D轉(zhuǎn)換后得到的數(shù)字信號(hào),DSP對(duì)輸入的數(shù)字信號(hào)進(jìn)行處理,并經(jīng)過一定的計(jì)算和轉(zhuǎn)換得到相應(yīng)的能量。在DSP處理器中是按以下式進(jìn)行運(yùn)算的:
?????? * 電壓測(cè)量(有效值)計(jì)算式:
?????? 式中:U-電壓有效值,n-每周期采樣點(diǎn)數(shù),-電壓采樣值。
?????? * 電流測(cè)量(有效值)計(jì)算式
?????? 式中:I-電流有效值,n-每周期采樣點(diǎn)數(shù),-電流采樣值。
?????? * 單元件有功功率計(jì)算式
?????? 式中: P-單元件有功功率,n-每周期采樣點(diǎn)數(shù),-元件上電壓采樣值,-元件上電流采樣值。
?????? * 單元件無功功率計(jì)算式
????? 式中:Q-單元件無功功率,n-每周期采樣點(diǎn)數(shù),-元件上電壓采樣值,-元件上電流采樣值(移相后)。
?????? * 三相四線三元件有功功率計(jì)算式:
?????? 式中:-三相有功功率,-(i=A,B,C)各相有功功率。
?????? *三相四線三元件有功功率計(jì)算式:
?????? 式中:-三相無功功率,-(i=A,B,C)各相無功功率。
?????? 數(shù)字濾波的設(shè)計(jì)
?????? 數(shù)字濾波器運(yùn)算結(jié)構(gòu)的不同,將會(huì)影響系統(tǒng)運(yùn)算的精度、誤差、速度和經(jīng)濟(jì)性等性能指標(biāo)。在一般情況下,都要求使用盡可能少的常數(shù)乘法器和延遲器來實(shí)現(xiàn)系統(tǒng),并要求?
運(yùn)算誤差盡可能小。我們主要采用FIR結(jié)構(gòu)的滑動(dòng)平均濾波器(MovingAverage Filter)。
?????? 在數(shù)字信號(hào)處理應(yīng)用中往往需要設(shè)計(jì)線性相位的濾波器,F(xiàn)IR濾波器在保證幅度特性滿足技術(shù)要求的同時(shí),很容易做到嚴(yán)格的線性相位特性。為了使濾波器滿足線性相位條件,要求其單位脈沖響應(yīng)h(n)為實(shí)序列,且滿足偶對(duì)稱和奇對(duì)稱條件,即h(n)=h(N-1-n)和h(n)=-h(N-1-n)。
?????? 由此可見,F(xiàn)IR濾波器不斷地對(duì)輸入樣本x(n)延時(shí)后,再作乘法累加算法,將濾波結(jié)果y(n)輸出,因此,F(xiàn)IR實(shí)際上是一種乘法累加運(yùn)算器。在數(shù)字濾波器中,F(xiàn)IR濾波器的最主要特點(diǎn)是沒有反饋回路,故不存在不穩(wěn)定的問題;同時(shí),可以在幅度特性隨意設(shè)置的同時(shí),保證精確、嚴(yán)格的線性相位。穩(wěn)定和線性相位特性是FIR濾波器的突出優(yōu)點(diǎn)。下面是FIR濾波器設(shè)計(jì)的子程序:
.TEXT
?? BEGIN???? LDP? 80H,DP
????? LDI? @STACK_ADDR,SP
????? LDI? 21,BK
????? LDI? 19,RC
????? LDI? @XN_ADDR,AR1
????? LDI? @XNNEW_ADDR,AR2
????? LDI? @OUTNEW_ADDR,AR3
?? LOOP????? LDF? *AR2,R6
????? STF? R6,*AR1++(1)%
????? LDI? @HN_ADDR,AR0
????? CALL? FIR
????? STF? RO,*AR3
????? BR????? LOOP
?????? 數(shù)據(jù)處理方式
?????? 數(shù)據(jù)處理主要是對(duì)采集的離散化信號(hào)進(jìn)行運(yùn)算處理,利用快速傅里葉算法對(duì)電信號(hào)進(jìn)行分析(參圖 2所示)。
?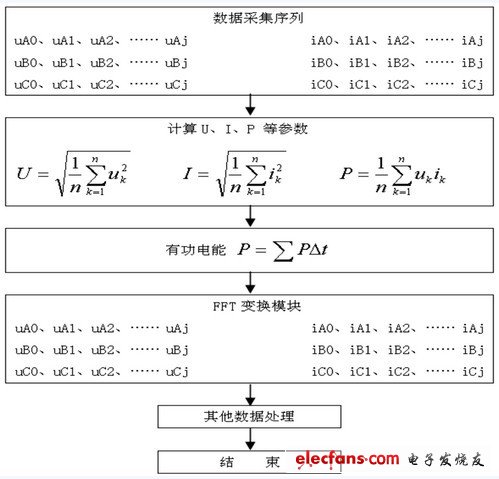
圖2? 數(shù)據(jù)處理
?????? 在DSP中最常用的方法是頻域分析法。對(duì)于一些序列長(zhǎng)度小的,通常采用離散傅里葉變換(DFT的精確定義為:X(m)=),而序列長(zhǎng)度大的,通常采用快速傅里葉變換(FFT)。FFT的運(yùn)算速度要比DFT的運(yùn)算速度快得多,但DFT的靈活性比較強(qiáng)。如果需要求出少量的頻域值,DFT方法可以比FFT運(yùn)算量小,數(shù)據(jù)序列長(zhǎng)度可以是任意的,并且N個(gè)輸出值的計(jì)算是相互獨(dú)立的。由于DFT的輸出是復(fù)數(shù),所以實(shí)部和虛部包含在兩個(gè)N長(zhǎng)度的數(shù)組中,對(duì)于輸出的結(jié)果可以通過計(jì)算機(jī)軟件(MATLAB)進(jìn)行仿真。計(jì)算和繪制DFT的輸出結(jié)果,通過FFT在DSP中的應(yīng)用,計(jì)算出N次諧波分量,從而提高了電能表上的各種技術(shù)參數(shù)。
 電子發(fā)燒友App
電子發(fā)燒友App




























評(píng)論