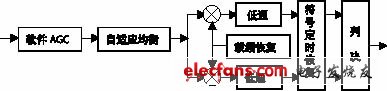
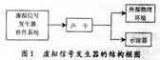
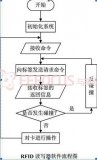
?

　　近幾年來，PC機的各項技術得到了迅速發展，CPU的計算速度、內存容量都大幅度提高，其數字信號處理能力已經完全可以滿足對常規通信信號的實時解調。將調制解調器設計在聲卡上而不是DSP芯片上，有很多好處：首先，聲卡廉價易得，充分利用卡上的line in、mic in、line out、spk out等端口，可以實現多路信號的實時解調，一卡多用;其次，優化后的解調軟件占用CPU的時間很少，可以在接收數據的同時從事其他工作;第三，不受存儲空間的限制，用高級語言編程，設計周期短。另外，這種設計方案與硬件平臺無關，軟件升級周期短。本文正是基于這種思想，拋開DSP器件，以PC機為硬件平臺，實現對QPSK信號的實時解調，系統框圖如圖1所示。

?

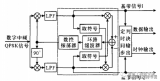
　　圖1中，接收機輸出的基帶信號經PC機聲卡采樣后得到離散化的數字序列。對信號的采樣可調用Windows的API函數對聲卡進行控制，包括采樣頻率、緩存大小、每次讀入的字節數等，具體實現可參看相關資料，本文不再贅述。圖1中的解調軟件部分是本文討論的重點，它完成對信號的數字化實時解調功能，其數字化解調原理如圖2所示。

?

　　軟件AGC

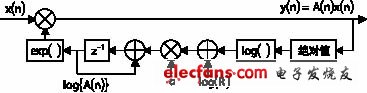
　　軟件AGC用于跟蹤信號外包絡變化實現對衰落的補償。本文采用圖3所示對數AGC。

?

　　圖3中的對數AGC用軟件實現時，A(n)的計算采用下式。

　　log{A(n+1)}=log{A(n)}+α[log{R}-log{|A(n)x(n)|}]

　　圖中，x(n)是軟件AGC的輸入信號，y(n)是輸出信號;A(n)是AGC的增益控制變量;α和R為常量，取值根據設計要求在補償速度和穩定性之間取折中，當要求補償速度迅速時，取較大的值，反之，取較小的值。

　　DFPLL載波頻率恢復

　　在位同步點附近，存在信號的碼間串擾問題。DFPLL的基本思想就是，對于每個碼元，利用位同步附近的采樣點計算碼元的相位，并根據基帶信號碼元的相位特點，計算出參考載波與信號載波的差值，利用此差值調整VCO的相位，進行載波恢復。

　　設QPSK信號的第n個碼元在位同步點處的相位信息為：，其中，i=0,1,2,3,θ(n)為第n個碼元的相位偏移。要得到相位誤差，需要去除相位信息中的信息分量πi/2，通過觀察QPSK星座圖可以發現，相鄰星座點間的相差總在π/2附近，于是用如下方法可以去除信息分量。令，并令，其中，mod表示求余，ξ(n)是單個碼元的相位誤差。如果采樣頻率為Fs，碼元速率為fb，則該碼元每個采樣點的平均相位誤差為e(n)=ξ(n)/(Fs/fb)。平均相位誤差送入環路濾波器，濾波結果由系數k調整后，送入VCO進行相位增量調整，當e(n)穩定在一個較小值附近時，DFPLL處于鎖定狀態。環路濾波器采用一階RC低通濾波器。由于其輸入為相位估計器，考慮來自相位估計器的相位差值信號以碼元速率fb變化，其截止頻率應在fb附近，用沖激不變法設計歸一化系統函數為：。濾波器的截止頻率和增益k對捕獲時間和環路的穩定性都有影響，調整這兩個參數，使之達到最佳狀態。

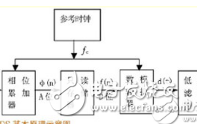
　　DTTL符號定時恢復

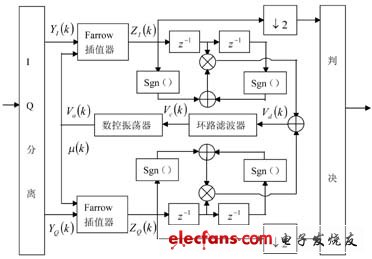
　　QPSK調制的DTTL符號定時恢復算法原理如圖4所示。該算法由Farrow插值器、定時誤差檢測器、數字環路濾波器及數控振蕩器等四部分組成。可以看出，它實際上是一個帶鎖相環的反饋定時誤差同步器。符號定時恢復主要是通過不斷調整Farrow插值器的參數，使得輸出的樣點值抽樣在每個符號周期的最大值上。該算法工作在2個樣點/符號。

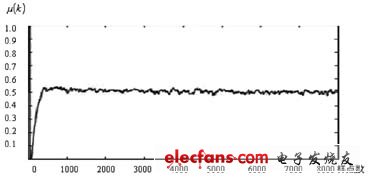
　　圖4中的Farrow插值器使用線性插值公式Z1(k)=(1-μ(k))Y1(k-1)+μ(k)Y1(k)，其中0≤μ(k)<1。調整μ(k)的值，即可使樣值采樣在最佳時刻。誤差檢測器可表示如下。

?

　　Vd(k)=Z1(k-1)[sgn(Z1(k))-sgn(Z1(k-2))]+ZQ(k-1)[sgn(ZQ(k))-sgn(ZQ(k-2))]

　　環路濾波器采用二階數字環路濾波器，其輸入輸出關系可表示如下。

　　Vc(k)=Vc(K-1)+KpVd(k)+(Ki-Kp)Vd(k-1)

　　關于比例增益常量Kp和積分增益常量Ki的選擇，可以參考文獻4。數控振蕩器的控制字Vo按照下式每個符號調整一次。

　　Vo(k)=Vo(k-1)+KoVc(k)

　　式中Ko為數控振蕩器靈敏度增益常量。最后，分數索引μ(k)可按下式更新。

　　μ(k)=mod(μ(k-1)+Vo(k-1),1)

　　式中mod表示取余。

　　Kalman DFE自適應均衡器

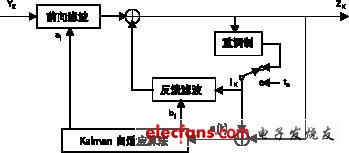
　　Kalman DFE自適應均衡器的均衡原理如圖5所示。

?

　　由圖5可以看出，DFE均衡器包含兩個橫向濾波器，一個橫向濾波器用于線性的前向濾波處理，其判決結果反饋給另一個橫向濾波器。如果前面的判決是正確的，則反饋濾波器就能消除由前面碼元所造成的串擾。反饋濾波器的抽頭系數由包括前向濾波器所造成的信道沖激響應拖尾所決定。不難理解，只要誤碼率小于1/2，原則上就能保證收斂。

　　圖中前向濾波器為M階，反饋濾波器為N階;tn為訓練序列;YK為前向濾波器的輸入，ai為其抽頭系數;IK為反饋濾波器的輸入，bi為其抽頭系數;ZK為DFE的輸出;e(k)為誤差信號。均衡器工作時，總是先由接收到的同步序列或訓練序列tn等已知序列進行訓練。在訓練期間，DFE均衡器將內部產生的理想信號作為反饋輸入信號，由LMS或RLS算法對信道進行估計，同時調整前向與反饋濾波器的抽頭系數，收斂到均方誤差最小。當殘差足夠小時，均衡器被切換到直接判決模式，即由判決符號重調制生成的參考信號作為反饋輸入，均衡器將繼續工作在均方誤差最小狀態。

　　由圖5可知，

　　令XT(k)=YK,YK+1,...,YK+M-1,IK-1,IK-2,...,IK-N)

　　WT(k)=(a1,a2, ..., aM,b1,b2, ...,bN)

　　其中，T表示轉置，則誤差信號e(k)表示如下。

　　e(k)=IK-ZK=IK-WT(k-1)X(k)

　　Kalman算法的精髓在于，已知W(k-1)，遞推計算W(k)，其遞推步驟如下。

　　初始化：0<ω<1;W(0)=0;P(0)=I，I表示單位矩陣。

　　for k=1 to n do ：e(k)=I(k)-XT(k)W(k-1)

　　K(k)= P(k-1)X*(k)

　　ω+XT(k)P(k-1)X*(k)

　　P(k)= [p(k-1)-K(k)XT(k)P(k-1)]

　　W(k)=W(k-1)+K(k)e(k)

　　其中，K(k)為卡爾曼增益向量，P(k)為X(k)的協方差矩陣。均衡器系數隨時間改變的量等于誤差e(k)乘以卡爾曼增益向量K(k)。因為是M+N維的，所以每一個抽頭系數實際上受到K(k)的一個元素的控制，從而獲得快速收斂。

　　實時測試結果

　　測試系統框圖如圖1所示。這里接收機輸出的PSK31信號的載頻為1000Hz，碼元速率為31.25波特，調制方式為QPSK，聲卡的采樣頻率為8000Hz。DTTL符號定時恢復過程中，定時誤差及分數索引的收斂情況如圖6、圖7所示。DFPLL載頻恢復過程中，VCO輸出參考載頻的收斂情況如圖8所示。圖9則分別顯示了未加均衡與加均衡時，解調出的QPSK星座的對比。

?

?