引言
數字信號處理現已在通信與信息系統、信號與信息系統、自動控制、需達、軍事、航空航天、醫療和家用電器等眾多領域得到了廣泛的應用。在數字信號處理應用中, 濾波占有十分重要的地位, 如對信號的過濾、檢測、預測等, 都要廣泛地用到濾波器。IIR數字濾波器的設計保留了一些典型模擬濾波器優良的幅度特性, 但所涉及的濾波器相位特性一般是非線性的, 而FIR濾波器則可在保證幅度特性并滿足技術要求的同時, 也很容易做到嚴格的線性相位特性。
1 基于窗函數法的FIR濾波器設計
1.1 單位沖激響應
首先應根據技術要求確定待求濾波器的單位沖激響應hd (n)。如果給出待求濾波器的頻率為Hd (ej), 那么單位取樣響應則可用下式求出:


如果給出通帶阻帶衰減和邊界頻率的要求,則可選用理想濾波器作為逼近函數, 從而用理想濾波器的特性作傅立葉逆變換, 以求出hd (n)。若理想低通濾波器為:

1.2 過渡帶及阻帶衰減
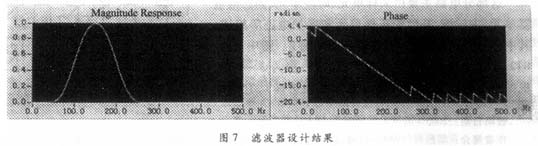
根據對過渡帶及阻帶衰減的要求, 設計時可選擇窗函數的形狀, 并估計窗口長度N。設待求濾波器的過渡帶用Δω表示, 它近似等于窗函數的主瓣寬度。由于過渡帶Δω近似與窗口長度N成反比。即N=A/Δω, 其中A決定于窗口形式, 例如, 矩形窗A=4π, 哈明窗A=8π等。按照過渡帶及阻帶衰減情況, 選擇窗函數形式。其設計原則是在保證阻帶衰減的情況下, 盡量選擇主瓣比較窄的窗函數。
1.3 單位取樣響應的計算:
計算濾波器的單位取樣響應h (n) 時, 可按正式進行:

驗算技術指標是否滿足要求時其設計出的濾波器頻率響應可采用下式進行計算:
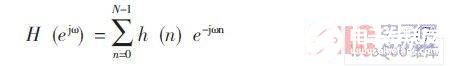
計算上式時, 可使用FFT算法。如果H (ejω)不能滿足要求, 那么, 根據具體情況, 可重復上述設計, 直到滿足要求為止。
2 基于DSP的FIR數字濾波器實現方案
2.1 濾波系統的差分方程
2.2 實現方案
由于在卷積運算之前, h (n) 的N個數值是已知的, 因此, 可先在程序存儲器中開辟N個單元來存放h (n)。由于輸入序列x (n) 是不斷變化的,因此, 在數據存儲器中可開辟N個存儲單元并對其進行移位寄存, 其初始值分別為x (n)、x (n-1)……x (n-N-1), 然后采用循環尋址的方法對其進行訪問。每次輸入新的樣本時, 可以以新樣本改寫滑窗中的最老的數據, 而滑窗中的其他數據則不需要移動。利用片內8 kB (循環緩沖區長度)寄存器可對滑窗進行間接尋址, 循環緩沖區地址首尾相鄰。8級循環緩沖區的結構如圖1所示, 其中頂部為低地址, 圖1中的(a) (b) (c) 分別為初始狀態、輸入1個和2個樣本后的存儲情況。
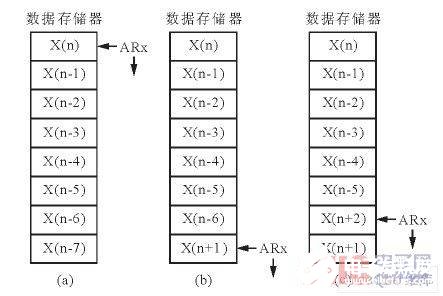
圖1 8級循環緩沖區結構。
3 仿真結果
下面是一組信號采樣序列樣本x (n), 其中存在有高頻干擾。現以x (n) 作為輸入序列, 然后濾除其中的干擾成分。
{x (n)} = {-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,*,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0}
本設計的線性相位低通FIR數字濾波器的截止頻率ωc為0.2πrad, 窗口長度N為11。根據上述原理及實現方案, 若采用漢寧窗來實現, 則可依據算式計算出用漢寧窗設計時的各h (n) 的系數:
{h (n)} = {0, 0.0045, 0.0349, 0.0991, 0.1692,0.2, 0.1692, 0.0991,0.0349, 0.0045, 0}
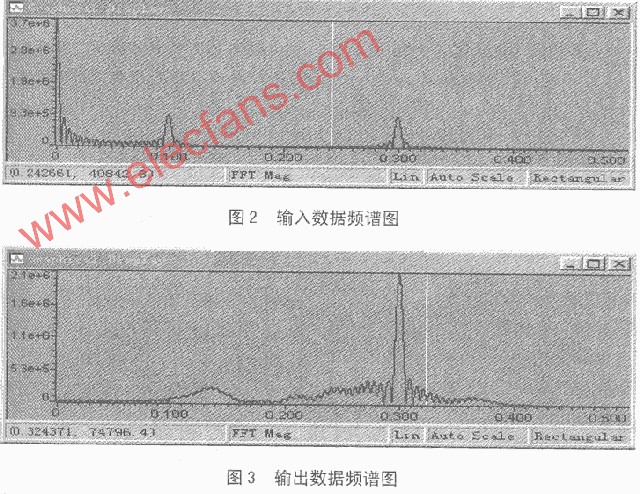
在CCS2.0軟件中觀察x (n) 的輸入曲線如圖2所示, 圖3所示是其y (n) 輸出曲線。
由圖2和圖3兩圖對比可見, 經過濾波后, 其輸入曲線變平滑了。并且, 根據計算所得:
{y (n)} = {0, -0.018, -0.1486, -0.4662, -0.893, -1.305, -1.7006, -2.1548, -2.6372, -3.0062, -3.1918, -3.3098, -3.5296, -3.8198,-4.009, -4.0482, -3.9514, -3.4596, -2.0672, 0.3162, 2.7908, 3.*8, 0.9464, -6.2018, -17.6736, -31.8884, -45.5584, -54.1796, -54.044, -44.916, -30.6*, -16.6756, -6.3676, 0.058,4.037, 6.5272, 7.5976, 7.318, 6.2854, 5.0906, 3.8896, 2.*2, 1.5078, 0.6238, 0.0788, -0.3198, -0.7348, -1.0768, -1.1474, -0.9538,-0.7342, -0.6852, -0.7*, -0.8172, -0.8136,-0.8834} 上面一共56個值。
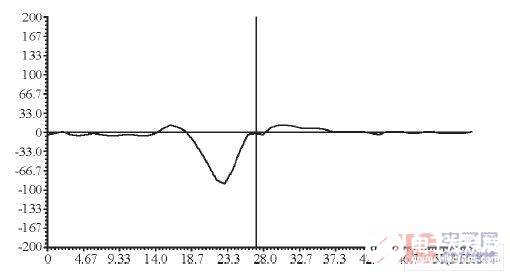
圖2 x (n) 輸入曲線
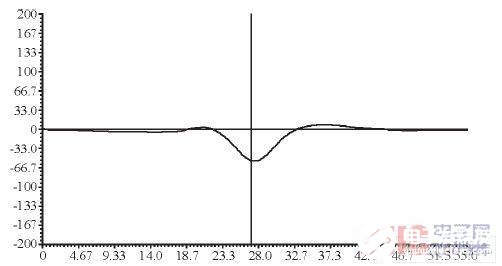
圖3 y (n) 輸出曲線
4 結束語
通過實驗結果可見, 本設計用DSP設計的FIR數字濾波器的輸出曲線對應值與計算所得值完全相符, 由此證明, 本設計的程序是正確的。
責任編輯:gt
 電子發燒友App
電子發燒友App










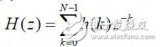





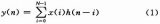
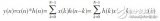
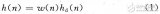











評論