DNN加速器的設計一直在兩個方面使力：通用架構和高效性能。通用性需要自頂向下的設計，首先綜合各種神經網絡的算子設計一套標準的指令集，然后根據硬件平臺的特點，考察計算資源，存儲資源以及帶寬，進行硬件的模塊化設計，在指令集以及硬件的特殊結構基礎上，再去構建工具鏈。

通用性要看的廣，指令集的定義要具有擴展性和靈活性，工具鏈要能夠靈活的對接不同的深度學習框架，能夠處理不同類型的網絡。這是一個很大的工程，需要一個頂級架構師以及大批軟件編譯類工程師合力來做。但是現在出現的很多開源工具鏈框架將這種開發難度大大降低了，比如TVM，LLVM，MLIR等工具給我們提供了基礎，避免了再造輪子的重負。很多公司也基于這些開源框架來編寫自己的編譯工具。

高效性能永遠是各大芯片廠商比拼的焦點，性能的提升需要三個方面共同努力：一個是來自于芯片的廣大的資源，包括計算資源和存儲資源，以及高帶寬，從Xilinx芯片不斷加大尺寸和DSP數量，以及采用HBM，還有GPU內核數量的提升以及對HBM的采用都說明了這個問題；另外一個是算法的深度優化，神經網絡對噪聲的容納能力讓其有了很多可以利用的空間，比如int類型的量化，稀疏化，剪枝等等，可以在保證精度的前提下，大大降低其運算量以及參數數量，同時能夠更好的適配硬件；第三就是需要編譯器對指令的優化，算符融合，無效算子的kill，指令的schedule等等，都會對最后性能造成很深的影響。提升性能需要看的深，追求硬件，算法，編譯的極限，盡最大可能利用硬件有限的資源，盡最大可能優化網絡的結構，盡最大可能尋求指令序列的優化解。今天我們談性能追求當中的一個很小的部分——DSP。

Xilinx DSP

1 結構和功能

DSP48E2是zynq器件中使用的DSP類型，其主要結構包括一個27bit前加器，27x18bit的乘法器，一個48bit的可以執行加減法，累加以及邏輯功能的ALU。如下圖所示：

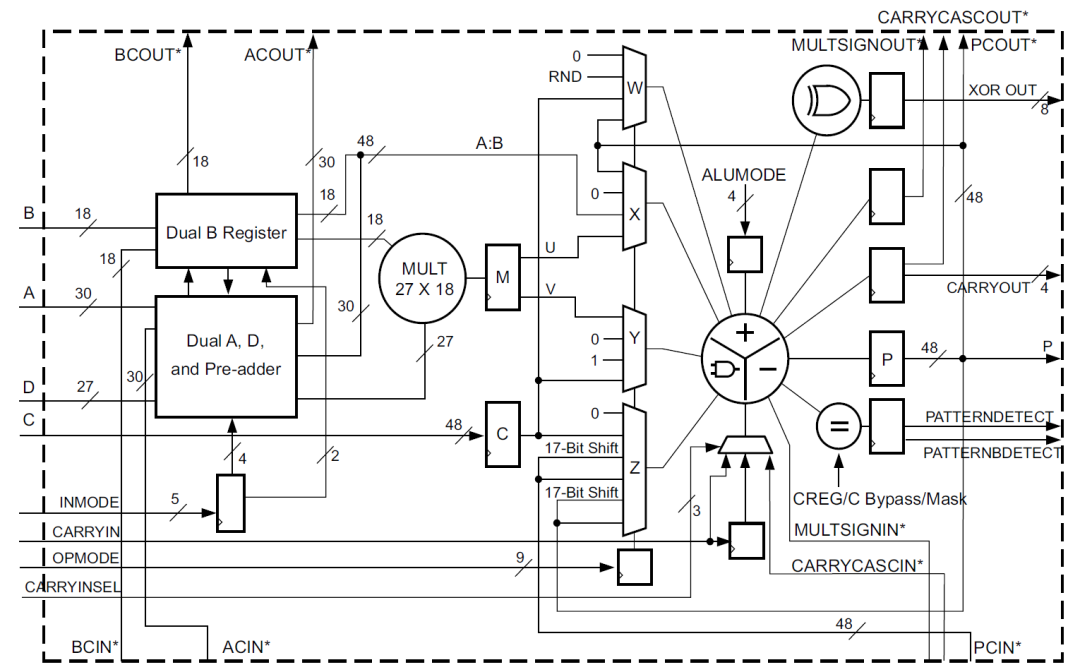
DSP48E2單元的功能包括：

1） 前加器可以計算D+/-A以及D+/-B的功能，這大大擴展了A和B端口的公用。通過對A和B的選擇，可以增加乘數的寬度，利用這個可以將神經網絡的算力提高一倍甚至兩倍，后邊我們具體再講。

2） 前加器可以將結果發送到乘法器，所以提供了平方操作，比如A*A。

3） A端口的低27bit用于乘法器輸入，30bit完整數據可以和B端口數據concate實現48bit數據的ALU操作，包括與或非等邏輯運算以及加減法計算。

4） 端口CARRYCASCIN和CARRYCASCOUT能夠用于多個DSP級聯，這對于實現神經網絡中的矩陣乘法或者卷積的累加非常方便。

5） 基于SIMD模式的加減法操作，可以支持2路24bit加減法以及4路12bit加減法。

6） 支持48bit的邏輯操作：and, or, not, nand, nor以及xnor。

7） 支持一些類型檢測：overflow/underflow，rounding等。

8） 支持17bit右移操作。

9） DSP單元是單時鐘同步運轉的，始終頻率能夠達到內部memory頻率的兩倍，相對內部邏輯，DSP可以工作在倍頻下。

DSP支持的操作類型很多，主要用于兩方面：一個是基于大量乘累加的計算，比如conv，gemm，FFT等。另外一種是純加減法和邏輯的運算，這些在神經網絡中也有很多，比如element-wise add。邏輯運算用的不多，更多可能作為一些計算的輔助。

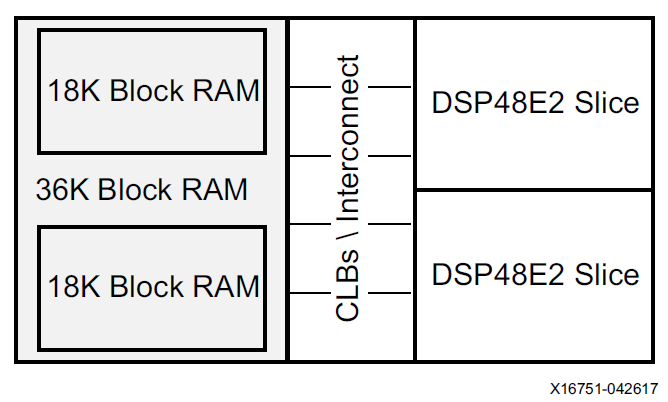
Zynq器件中通常將2個DSP48E2和一個36Kb的block memory以及5個CLB放置在一起，一個36Kb的BRAM可以拆分成2個18Kb的memory使用，每個memory可以獨自被一個DSP占用。這樣的配置也為DSP以及存儲的高效配合使用提供了模板。后邊我們可以利用這樣的結構構建一個conv計算單元。同時多個DSP在FPGA芯片內部是垂直擺放的，這有利于多個DSP的cascade。

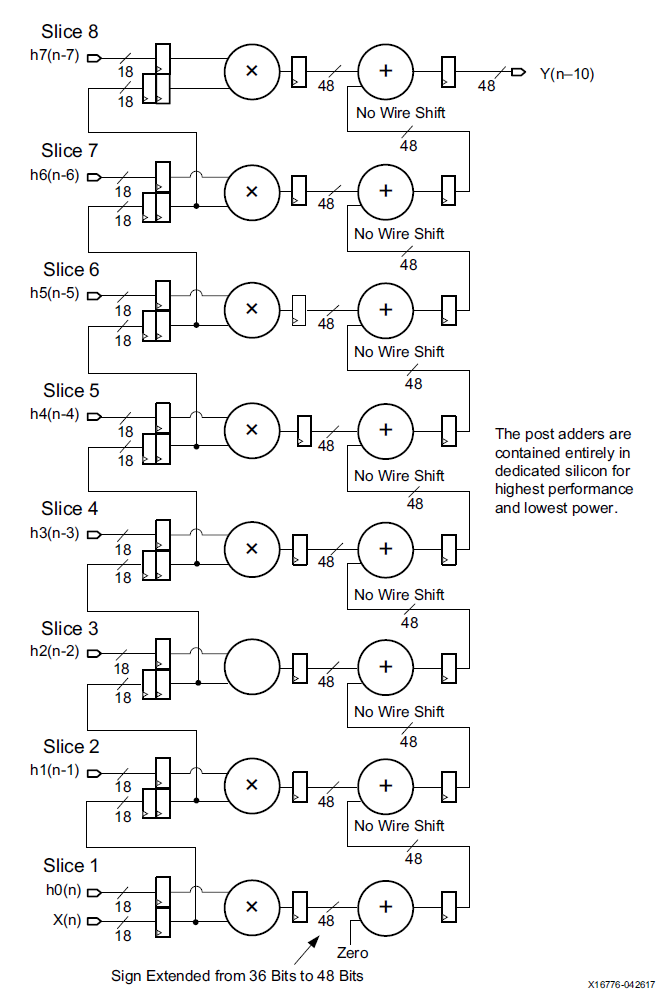
現在來看一下如何使用DSP陣列來構建低功耗的加法樹。在傳統的FIR濾波器中，乘累加的普遍做法是將多個乘法的輸出通過多級加法器累加起來，需要的加法器級數是計算數據量的log2函數。比如一個如下濾波器：

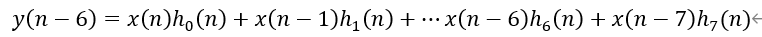
使用加法樹會采用這樣的結構：

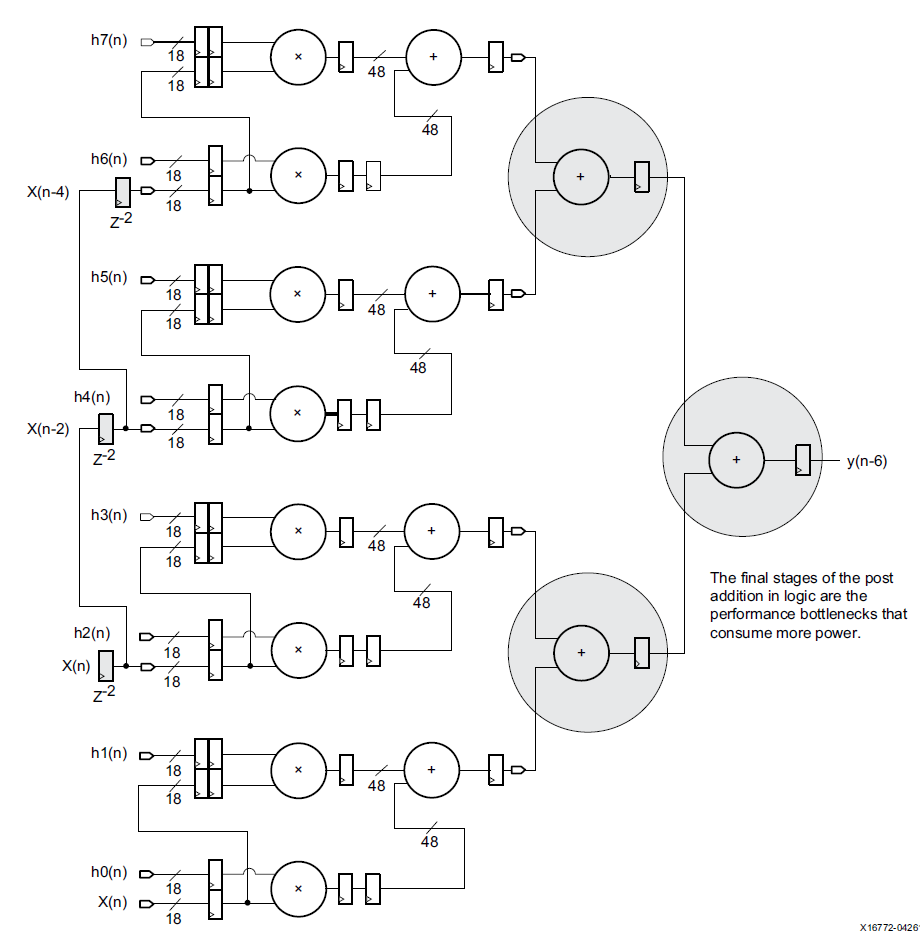
這樣的加法樹會消耗更多的資源，代價以及能耗。特別是后幾級的加法器位寬變的越來越寬，對LUT資源消耗很多。如果我們利用DSP的級聯功能，可以完全實現FIR中的多輸入加法功能。DSP中提供的post-adder以及CARRYCASCIN和CARRYCASCOUT可以選擇上一級DSP的輸出，同時將本級輸出作為下一級輸入。但是要注意級聯的長度收到post-adder加法器位寬的限制，對于48bit的post-addr，如果乘法的輸出長度為32bit，那么其級聯長度可以達到2^16。

2 conv實現

CNN中一個卷積層的feature map有三個維度：長(H)，寬(W)，輸入通道(I)。輸出的feature map也同樣有三個維度長(H)，寬(W)，輸出通道(O)。卷積核的維度就是4個維度：對應著feature map的H，W以及I和O。一個輸出通道O的feature map是每個輸入通道feature map的卷積結果的和。

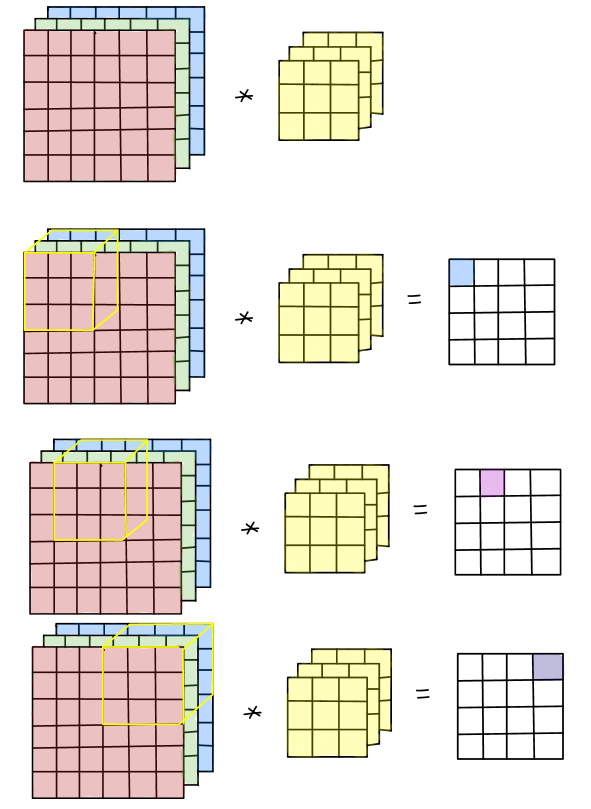
依據這樣的運算特點，我們首先利用DSP的垂直結構和cascade特性構建一列運算單元，這個計算鏈包括DSP，BRAM以及一些LUT邏輯，每個DSP的輸出作為下一級DSP的輸入。DSP的端口A和D分別用于kernel和feature map數據的輸入，kernel參數存儲在BRAM中，36Kb BRAM作為2個18Kb BRAM使用，這樣每個DSP都獨自占用一個存儲單元。我們以3x3卷積為例（stride為1，3輸入通道），DSP陣列以及計算結構如下圖所示：

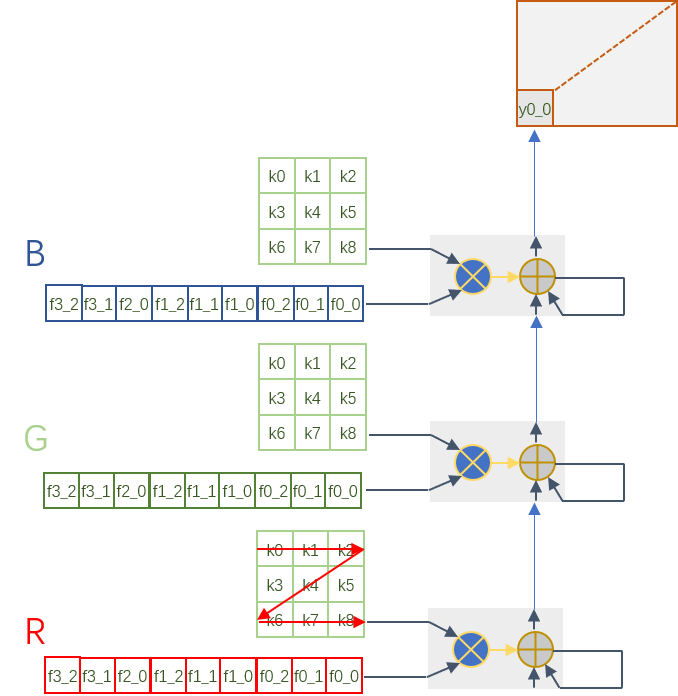
每個BRAM中存儲9個核參數，按照先H后W的方向讀取送入DSP，feature map相對應的按照3x3卷積計算方向讀取，先讀取一個窗的數據，計算出一個元素結果，然后滑窗讀取下一個窗的數據。每個DSP輸出和下一次DSP的結果進行累加得到一個窗卷積的結果，然后這個結果再傳遞到下一個DSP用于feature map不同通道之間的求和。這里面有幾個方面要考慮到：第一個是從一個DSP傳遞到下一個DSP有時間延遲，所以下一個DSP再進行通道之間數據求和的時候要有延時，這個可以通過延時讀取kernel和feature map來處理。同時需要有使能信號控制DSP輸出用于自身累加還是送入下一個DSP計算。當每個36Kb BRAM被拆分為2個18Kb BRAM的時候，18Kb BRAM讀寫公用相同口，所以將kernel寫入bram的時候和從BRAM讀數不能夠沖突，當然這個可以通過使用ping pong buffer來解決。

我們現在通過一列的DSP可以實現一個輸出通道的卷積計算了，如果我們沿著橫向增加DSP列數，就可以實現多輸出通道的卷積計算了。Feature map每個輸出通道是共享的，因此數據可以沿著橫向廣播到其它列來進行計算。

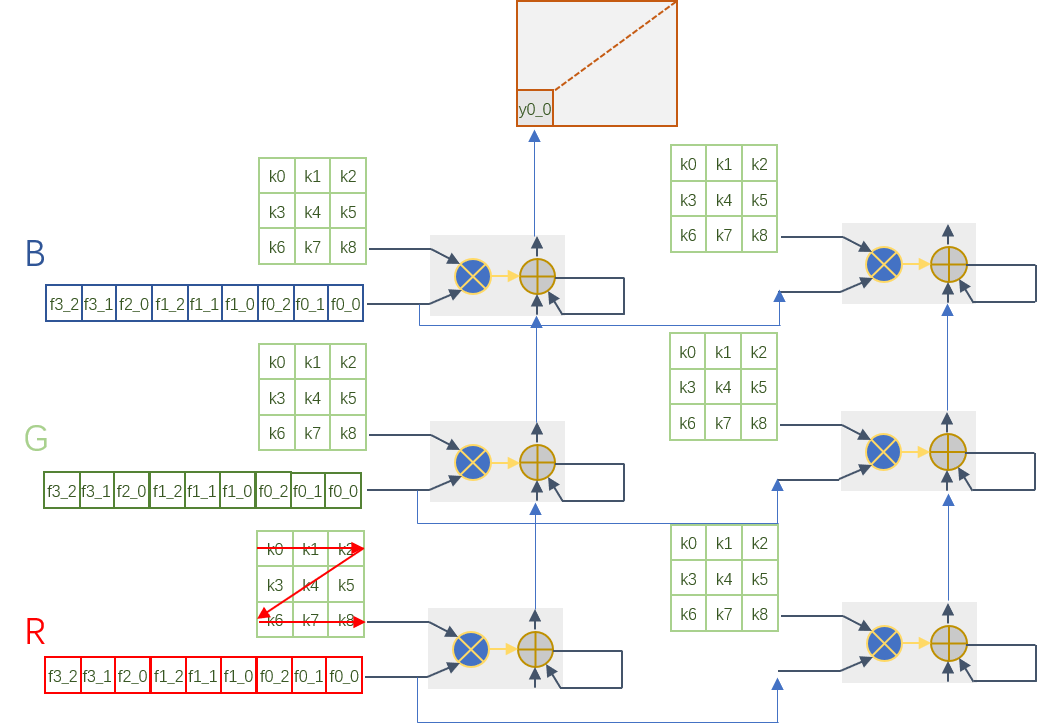
3 乘法器復用

INT16，INT8和INT4是神經網絡經常量化的數據類型。DSP48E2的乘法器是27x18的，因此INT16xINT16的只能同時計算一次。但是對INT8和INT4可以利用DSP的前加器實現乘法計算次數的翻倍。

我們發現兩個INT8乘法結果位寬是16bit，因此我們可以利用pre-adder將兩個INT8數據打包在一起。使得multiplier的27bit端口包含兩個INT8數據。如下公式表達了計算過程：

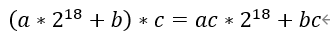
因為bc數據位寬為16bit，所以ac和bc的數據區分開了。我們從結果中取出低16bit作為bc的結果，而ac的結果受到了bc符號位的影響，其值相當于減了一個符號位數值，所以要獲得ac的結果需要取出偏移18bit結果加上符號位數值才是最終結果。如果符號位為1，則+1，如果符號位為0，則直接提取出來就可以了。

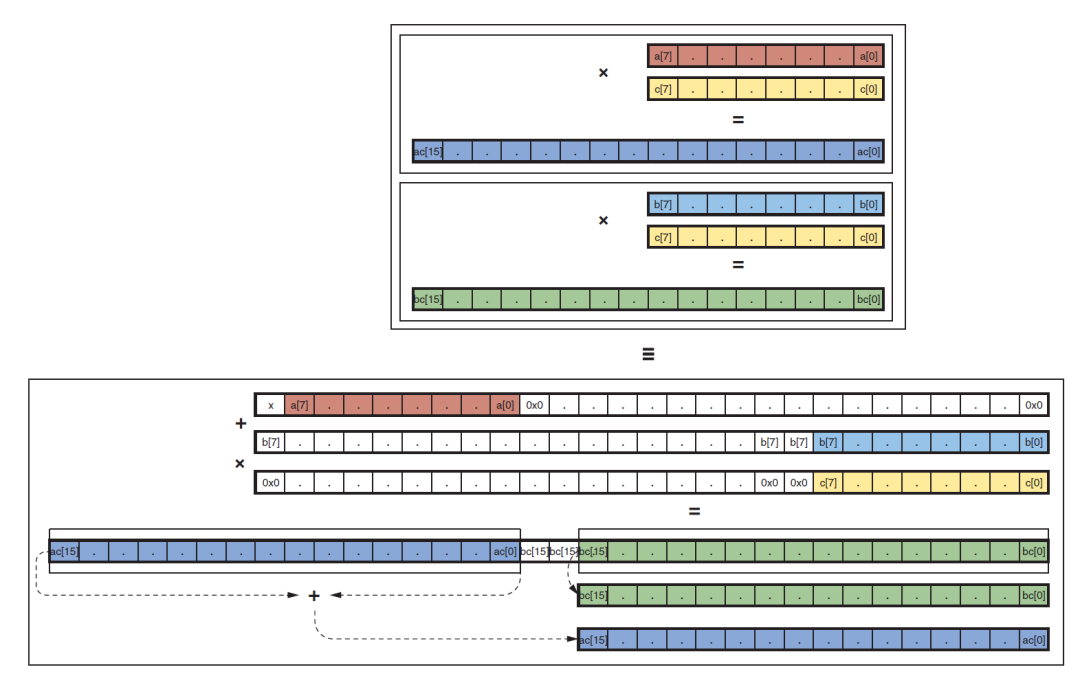
運用同樣的思路，我們能夠實現4路INT4的乘法，方法如下：

1） 利用pre-adder打包兩個INT4數據，然后再利用B端口拼接兩個正數數據。這種實現可以針對任何符號數據的乘法，因為pre-adder打包的數據可以有符號，所以我們可以通過轉換將B端口數據的符號位轉換到pre-adder端口上來。

2） 需要對打包的數據進行偏移，偏移保證4個結果不會發生混疊。可以進行如下偏移：

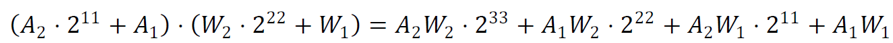
這樣低8bit就是A1*W1的結果，然后依次取出其它結果，同時加上符號位。

通過以上的處理，可以最大化利用DSP的計算能力，實現1個INT16，2個INT8和4個INT4的乘法。DSP的頻率通常都高于外部邏輯和BRAM的頻率（DSP最高頻率是BRAM頻率的2倍），所以可以讓DSP工作于高頻，而外部邏輯工作于低頻，這樣能夠讓DSP的計算再有所提升。BRAM以2倍的數據位寬供數，而DSP以倍頻方式工作，實現計算的增倍。那么相對于低頻工作時鐘來說，DSP就可以實現2倍INT16，INT8，INT4的乘法了。

Intel Stratix 10 DSP

對Intel的DSP沒有使用過，這里就根據其官方文檔進行一些淺顯的了解吧。相比于DSP48E2，Intel的DSP計算功能更為強大，可以同時支持可變精度的頂點計算以及單精度浮點計算，浮點計算在DSP48E2中是不支持的。其定點計算功能包括：

1） 支持18bit和27bit的位寬。

2） 能夠實現兩個18x19和一個27x27的乘法運算。

3） 內部有加法器和減法器，能夠實現兩個乘法結果的求和，還有64bit累加器實現歷史結果累加。

4） 有cascade級聯，用于多DSP block串聯，這已經是DSP普遍的拓展功能。

5） 內部含有寄存器組用于儲存參數，特別適用于filter操作。

6） 支持rounding。

浮點計算功能包括：

1） 支持通常的浮點乘法，加法，減法，乘加和乘減等。

2） 支持同級聯累加結果的乘法。

3） 支持復數乘法。

4） 支持一些異常報錯。

5） 支持vector的點乘操作。

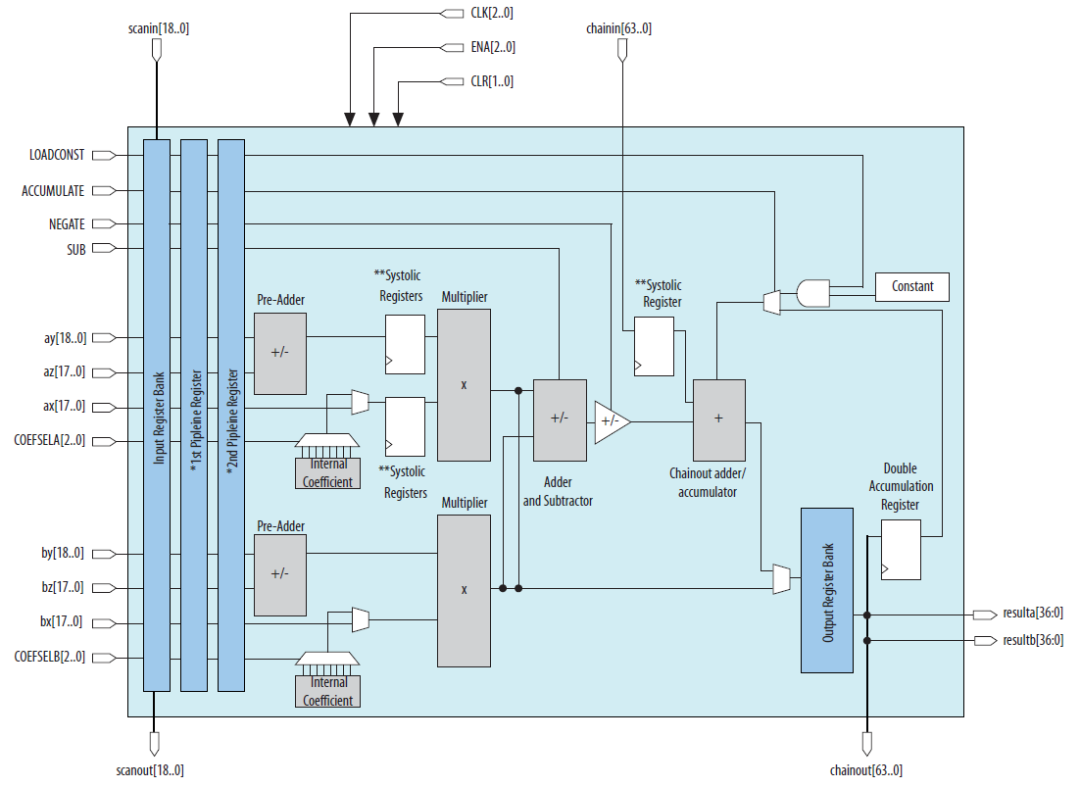
在雙18x19乘法模式下，結夠如下圖：

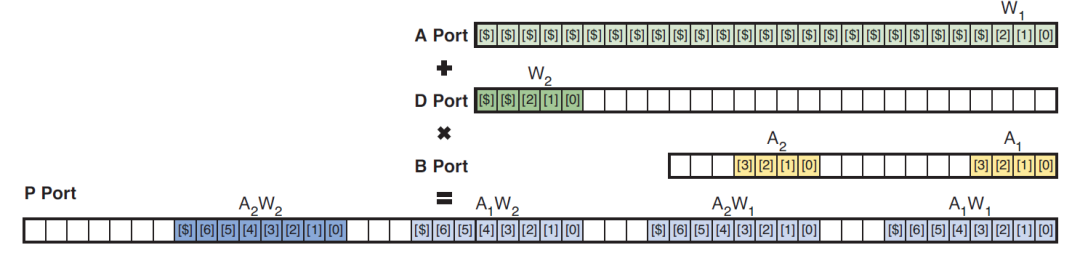
前加器能夠選擇性實現加法或者減法，也可以通過internal coeficient模塊控制input和內部參數的選擇，內部參數能夠支持8個不同的常數參數。雙18x19的乘法結果可以通過post-adder實現求和，也可以將結果獨立輸出。利用這種模式能夠實現復數計算，僅僅需要兩個DSP就可以實現，如圖：

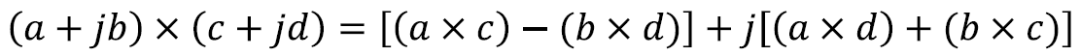
在雙乘法模式下，可以支持2個INT16乘法，2個INT8和4個INT4乘法。而在27x27模式下可以支持1個INT16，2個INT8和4個INT4的乘法。

在浮點模式下，DSP可以支持浮點數乘法，加減法以及MAC。同時還支持浮點數計算報錯，有助于計算中的debug。在乘法模式下，支持的異常有：mult_invalid（浮點乘法操作過程異常，導致結果不正確，這個時候結果會是NaN），mult_inexact（結果是rounded的，超過極大值或者極小值），mult_underflow（結果下溢），mult_overflow（結果發生上溢）。加法模式下支持的異常也有類似情形：adder_overflow, adder_underflow, adder_inexact, adder_invalid。而MAC模式下支持乘法和加法的所有異常檢測。

前邊梳理了Xilinx和Intel DSP硬核的功能和用法，但是我們還不知道DSP其內部的核心模塊乘法器是如何設計的。加法器我們知道有很多設計方法：串行加法器，并行加法器，相對邏輯和算法都很簡單。乘法器的設計相對就復雜了，接下來來研究一下。

乘法器

1 Baugh-Wooley算法

Baugh-Wooley是很古老很經典的一個乘法器算法，最早追溯到1973年，由Charles R.Baugh和Broce A.Wooley提出。1973年的時候大規模集成電路已經發展起來了，Intel已經造了第一個微處理器4004。中國當年集成電路產業剛剛起步，那個時候才開始自己研制的第一塊PMOS電路，同年引入外國單臺設備并開始建設自己的工藝線。這個時候距離FPGA出現還有10年的時間。

乘數和被乘數使用二進制補碼表示如下：

其中an和bn是符號表示，1表示負數，0表示正數。ai和bi是A和B中實際數值的表示。A*B在二進制補碼表示下結果為：

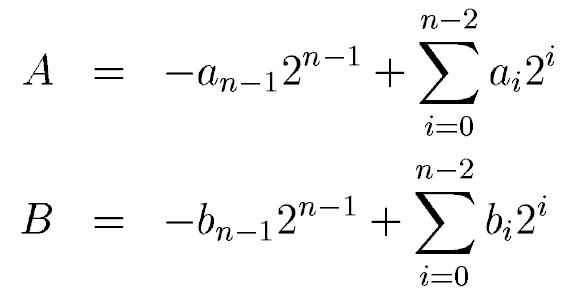
從上邊方程看出，結果中有加法也有減法，這是不統一的，不適合硬件的設計。Baugh-Wooley算法的核心就在于對減法的轉換，抓換為加法就可以使用加法器來實現部分結果的求和了。如果將后兩項的減法作為數據的負數符號位，用二進制補碼表示，就能夠轉換為和前兩項一樣的加法，如下：

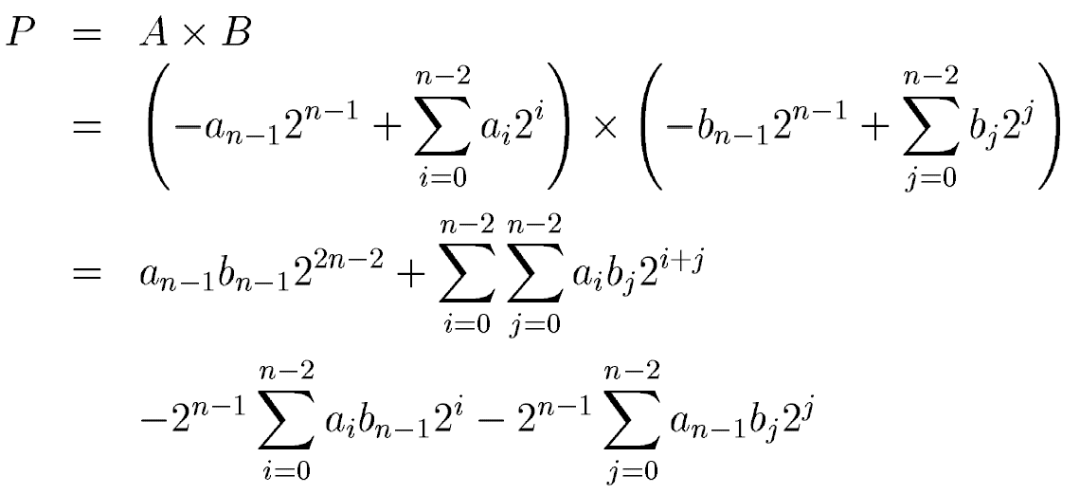
這樣我們就可以設計出基本的4:2 compressor來作為乘法器的基本單元，這個compressor如下：

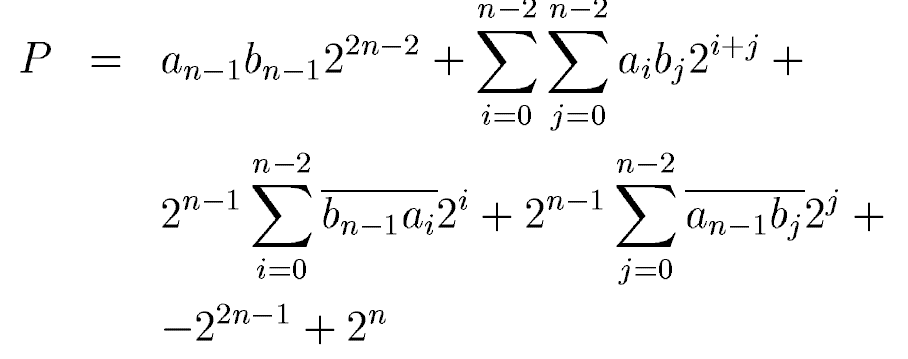
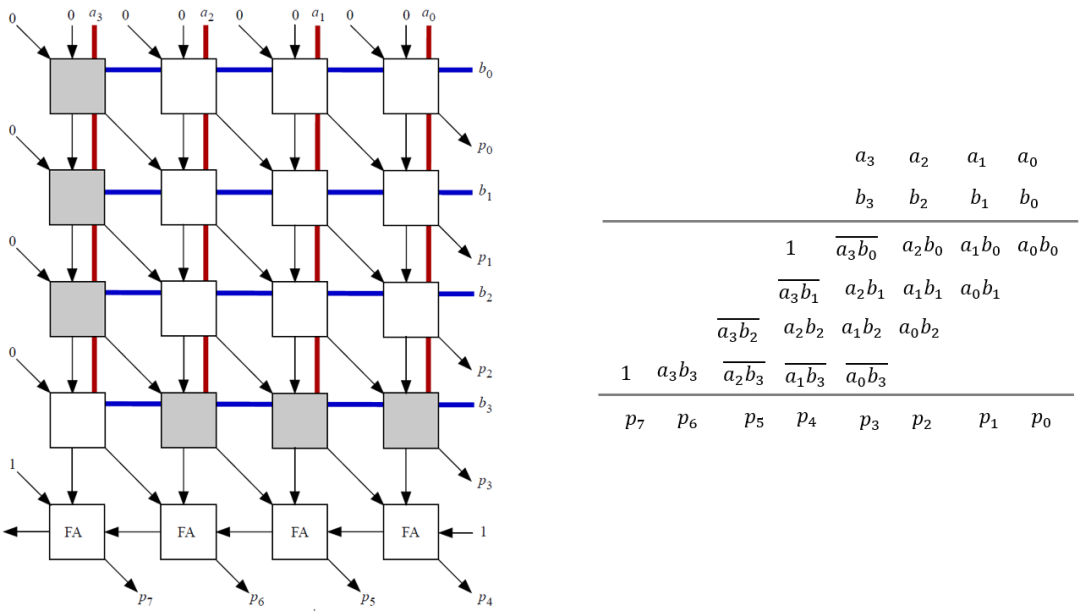
灰色單元是用于處理減法項的，這樣我們就能夠用一個二維陣列來構建一個乘法器了，比如對于4x4乘法有：

對于部分和邊界需要對數據取反，同時還需要附加上上式的最后兩項，對應著兩個“1”。對于一個nxn的乘法來說，部分和有n個，所以最長級聯鏈為n。這種乘法器隨著數據寬度的增加級聯線性增長，這會影響其延時。

2 基于Baugh-Wooley算法的可變位寬DSP設計

降低深度學習推理階段的精度表示不僅僅可以改善加速器性能，而且可以降低模型存儲以及DDR帶寬需求。對于量化精度更寬的深度學習模型來說，FPGA的可編程性提供了更為靈活的bit寬度適配，這相比于其它硬件平臺有更大優勢。但是目前Xilinx和Intel中嵌入式硬核DSP的bit位寬固定（只支持18bit以下數據乘法），不能夠有效的利用DSP資源來打包低bit數據乘法。于是有人從這一點出發來設計可變位寬乘法的DSP結構。本篇就介紹一篇基于Baugh-Wooley算法的改進的DSP結構。我們重點關注其實現27x27，18x18，9x9以及4x4乘法的方式和結構。

1 DSP基礎版。

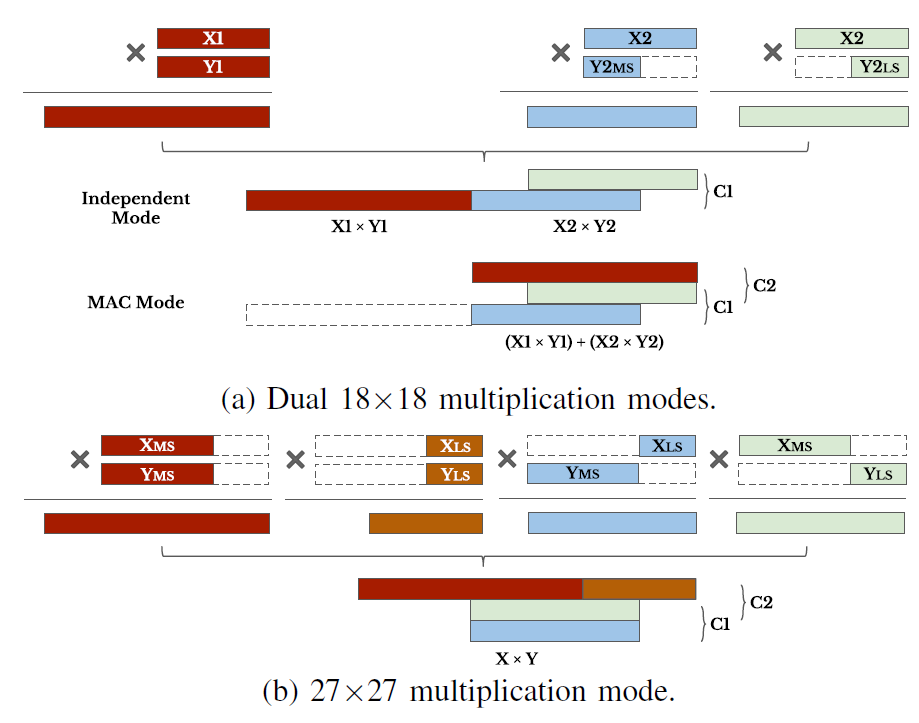
基礎版結構類似于Arria-10器件中的DSP結構，其可以支持雙18x18以及單路27x27乘法和累加（見下圖）。它包含4個乘法器M1（18x18），M2（9x9），M3（9x18），M4（9x18）。乘法器M1以及M4輸出有shift模塊，這塊可以用于實現乘法結果的分離。同時還添加了基于4:2compressor的加法器，可以支持多種計算模式（比如不同路乘法的求和等）。在雙路18x18模式下，M1可以執行一個18x18的乘法計算，另外一個18x18的計算需要M3和M4乘法器進行配合，Y（其中一個乘數）可以被拆分為兩部分（各9bit）用M3和M4執行乘法，然后在C1處完成求和。如果兩路乘法結果要求和，可以通過C2實現，如果要輸出兩路結果，那么可以bypass C2。在27x27模式下，四個乘法器都被用到，依然采用類似的辦法“分而治之”，將數據拆分為18bit和9bit，利用組合和移位實現。這里就不細說了。

2 DSP加強版。

對于比18bit更低的乘法計算，基礎版本只能將數據拓展為18bit來進行計算，這樣不能夠有效利用DSP資源。這對于功率消耗很高的DSP來說存在巨大的功耗浪費，代價巨大。為了支持低bit乘法，需要對基礎版進行改進。改進有以下幾個挑戰：

1） 改進版也必須兼容27x27和雙18x18模式。

2） 保證輸入輸出接口不會增加，避免模塊面積增大以及布線壓力。

3） 改進版工作時鐘不能低于600MHz（這是28nm器件DSP的普遍頻率）。

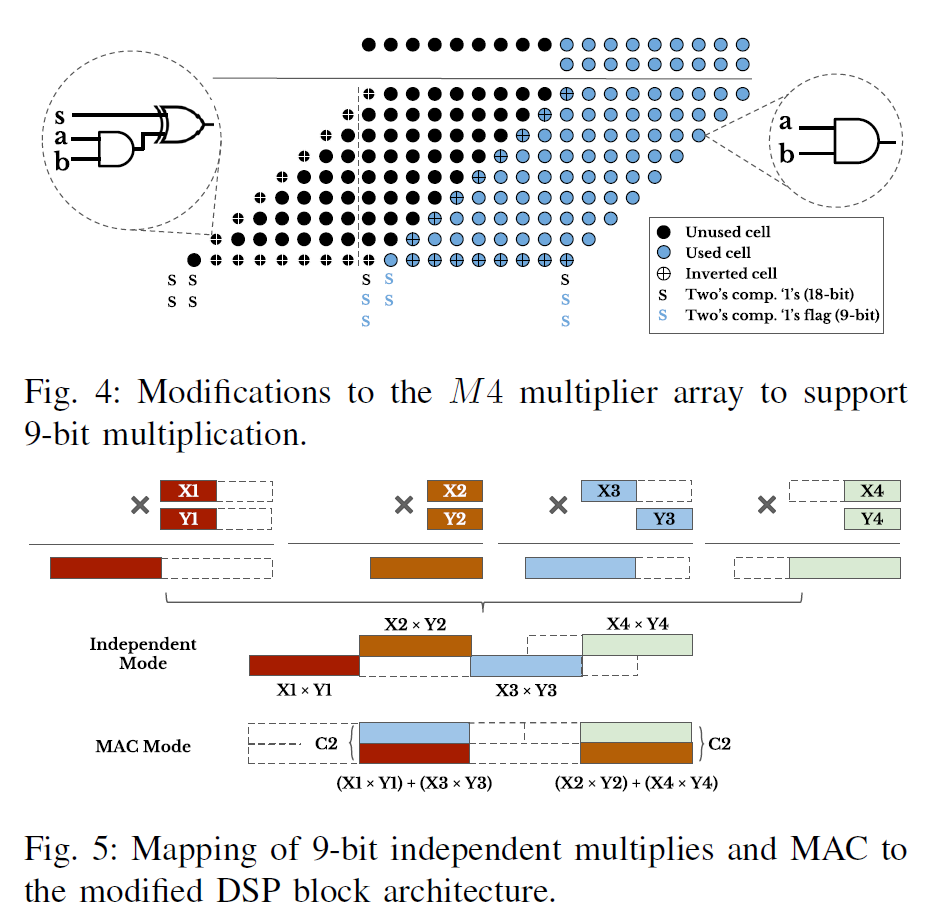
先看9x9bit計算支持，根據72bit的輸出端口，最大可以支持4個9x9計算（每個9x9輸出18bit位寬，所以最高是4個乘法）。M1的輸入最高位可以放有效的9bit數據，可以執行一個9x9乘法，M2也可以執行一個9x9乘法，因為M1有效結果向左偏移了18bit，不會和M2的重合，所以這樣就實現了兩個9x9乘法。關鍵在于M3和M4，其是18x9的乘法器，M3使用高9bit，M4使用低9bit，兩個乘法結果還是會存在數據交疊。一種辦法就是該進M4乘法器，使得其可以支持9x9乘法。改進的辦法就是修改乘法器中基本Baugh-Wooley計算單元。需要將9x9乘法部分和的邊界的cell修改為灰色（見Baugh-Wooley算法介紹）的cell。為了還能夠兼容18x9的乘法，就需要有一個配置開關，來控制邊界cell的模式。這回增加一些邏輯。

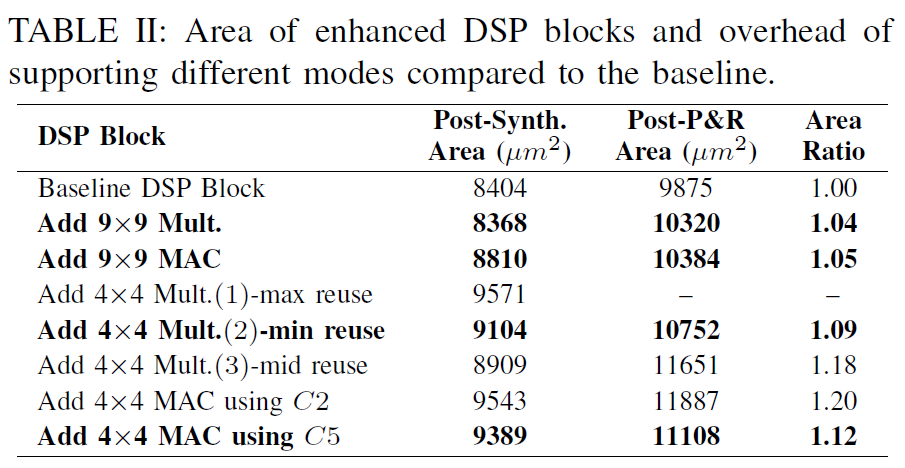
對于4x4的乘法，作者增加了4給4x4乘法器，同時修改M2和M3乘法器，使得其可以支持兩路的4bit乘法，這根據Baugh-Wooley的結構去修改是可行的。我們可以選擇去將一些無效的結果屏蔽掉來滿足這種要求。這加強版DSP就可以執行8個4x4乘法了。雖然M1和M4是空閑的，同時增加了4個4x4乘法器，但是能夠以最小的面積和邏輯代價換來計算性能的以倍提升也是值得的（可以看幾種模式的芯片面積和邏輯）。

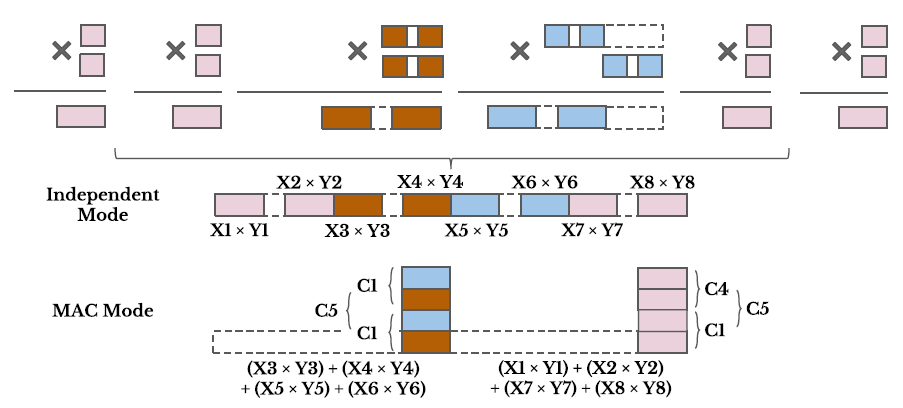
3 Booth算法

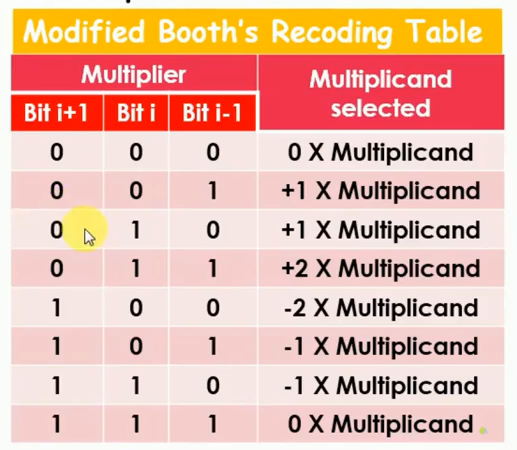
Baugh-Wooley算法中部分和進位鏈較長（等于乘數的位寬），這會限制乘法器的大小。A.D.Booth通過一種巧妙的辦法可以減少部分和結果，大大降低了部分和求和的鏈路長度。其基本思想是對乘數（multiplier）重新編碼，而被乘數（multiplicant）不變，以此降低乘數的位數。比如radix-2模式下，每2bit數據會被encode為0，1，-1三種數據類型，經過encode，乘數中連續為1的部分就會被0替代，而其它部分則不變，經過這樣就大大降低了部分和數目。具體過程如下：

1） 在乘數最后一位添加0，然后觀察乘數位數是否為2的倍數，如果不是最高位擴充符號位；

2） 從右至左依次遍歷每兩個bit位；

3） 進行如下encoder：00，11 -> 0，01 -> 1, 10 -> -1。

4） 然后使用encode的乘數和被乘數進行乘法計算。0和被乘數結果為0，這樣就節省了一個部分和，因此對于連續111的數據，就可以節省了部分和的計算。1和被乘數y結果y，-1和y結果為-y，-y可以轉變為二進制補碼形式，這樣就將減法轉化為加法。之后使用加法樹將這些結果加起來就可以了。

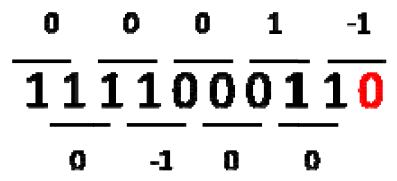
用的最多的是radix-4算法，其將連續的3bit數據encode為0，1，-1，-2，2表示。因為2的乘法只需要將數據左移一位就可以實現了，所以實現起來簡單。而-2是結果移位后取補碼結果，也容易實現。因此radix-4算法用途很廣。Booth算法減少了加法進位鏈，能夠實現更快速的乘法運算。

4 基于Booth算法的可變位寬DSP設計

選擇radix-4作為乘法器基本單元有一個巨大的優勢是：在保持乘法計算簡潔的同時，將部分和數目降低了一半。一個基本的Booth乘法器結構如下：

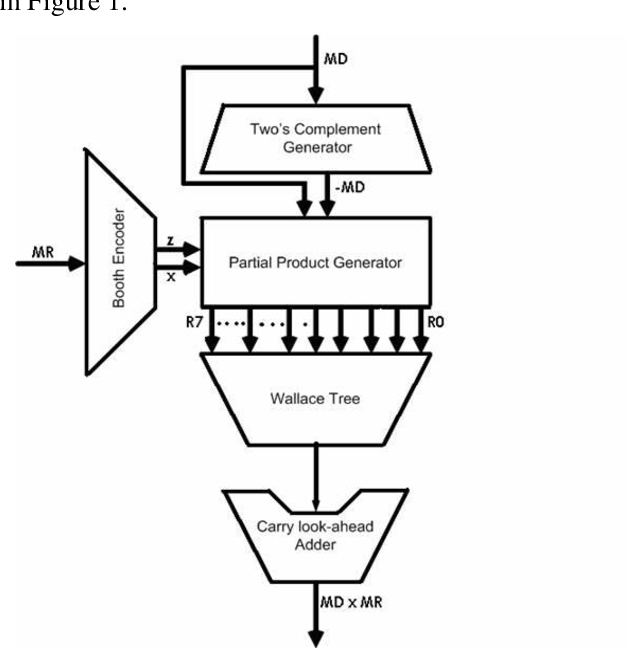
Booth encode的具體操作是：將最低bit后邊補0，然后每三個數據遍歷，按照表格encode為（0，1，-1，-2，2）中的數據，然后向左移動2bit，再進行3bit數據encode。然后計算encode后的multiplier和multiplicant的乘法。

看看作者如何通過對部分和生成模塊（PPG）的一個簡單修改來實現可變數據位寬乘法的。PPG的基本結構如下圖所示：

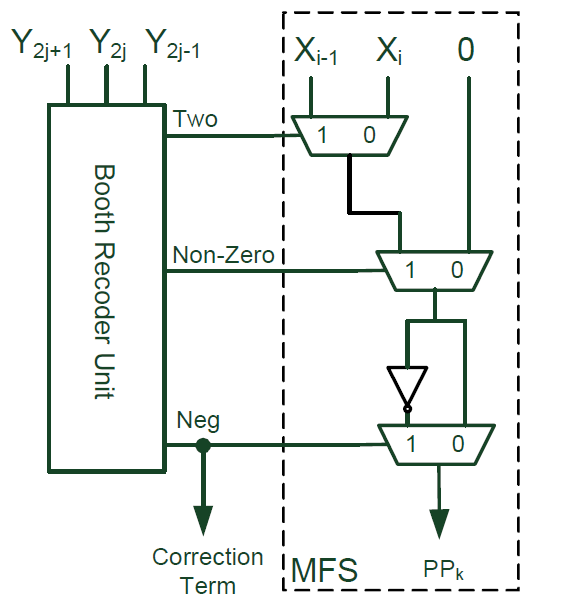
其中當encode值為負數的時候，符號位需要參與到部分和求和（PPR）中，作者將這個correction term傳遞到PPR中進行計算。由于Booth算法需要對每一個bit乘數進行encode，因此當位寬發生改變了的時候，就需要在符號位和encoded位進行選擇，這樣對于不同乘數位寬的配置來說，就需要很多multiplexer。一個簡單有效的辦法是先清除部分結果中的符號位擴展。我們可以給符號擴展位加1，加1之后符號擴展位就變成了一個inverted數。這樣部分和中的符號位就可以用0和一個inverted的符號位替代。而在部分和求和后面在通過-1來實現。所有部分和擴展位-1可以綜合起來用一個常數替代。

而通過對PPG模塊的一個簡單修改就可以達到這個目的，就是增加兩個信號：

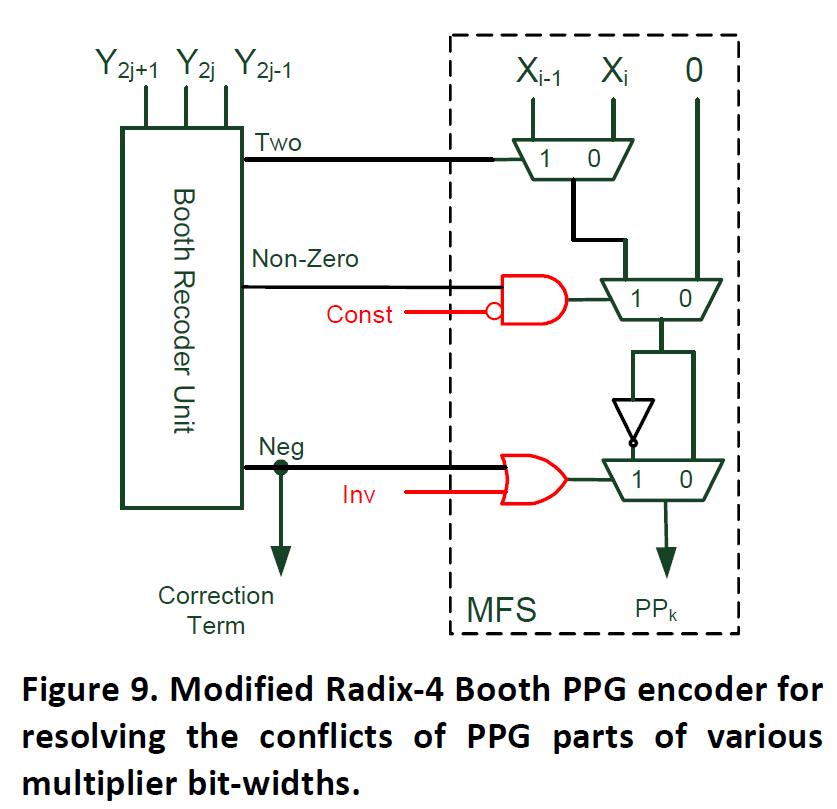
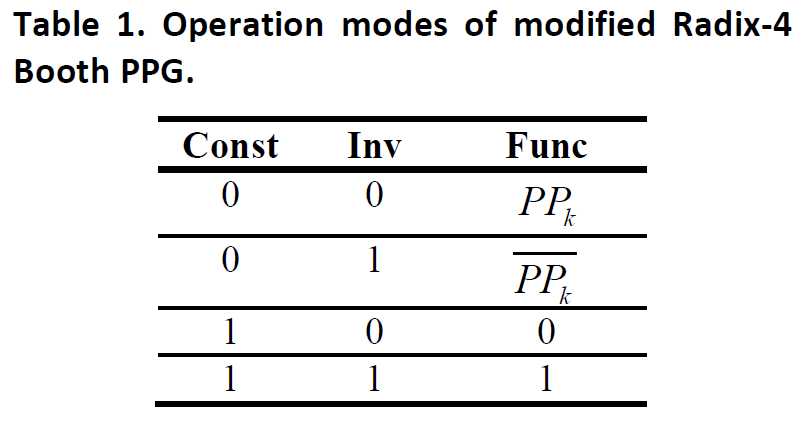
這樣我們就可以實現高效可變位寬乘法器。

審核編輯：劉清