步進電機控制器電路
2010-02-05 15:32:40 2478
2478 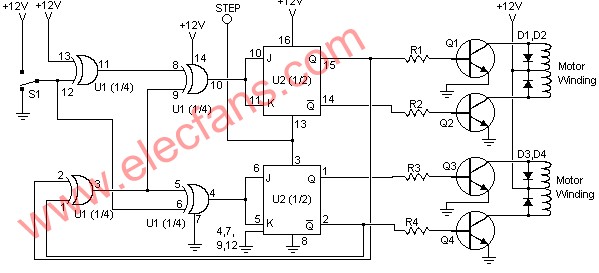
本文介紹了一些重要的步進電機相關技術,為開發人員基本了解步進電機的工作原理提供了足夠的信息,同時也介紹了用微控制器或數字信號處理器控制 步進電機 的方法。 步進電機也
2011-09-08 11:46:58 2893
2893 
在本教程中,我們將步進電機與PIC微控制器PIC16F877A連接。
2022-11-15 17:25:10 1016
1016 
parameters of the controller setup program have been completed in subroutine.子程序中完成了激光器、程控衰減器和樣品移動臺的步進電機控制器...
2021-08-31 08:44:22
用單片機設計一個步進電機控制器。要求能對步進電機實現正、反轉及速度控制,同時能對步進電機進行位置控制,即能控制步進電機從一個位置精確地運行到另一個位置。步進電機為四相反應式,軟件生成脈沖序列,可設
2012-12-08 15:50:26
用單片機設計一個步進電機控制器。要求能對步進電機實現正、反轉及速度控制,同時能對步進電機進行位置控制,即能控制步進電機從一個位置精確地運行到另一個位置。步進電機為四相反應式,軟件生成脈沖序列,可設
2013-03-20 16:48:37
步進電機控制器總結一、整體框架:系統在通信方式時支持主從控制二、系統原理1、 控制信號模塊電機控制信號:EN——>電機使能信號,只有當該信號有效的時候,步進電機才會工作DIR/CP+——>
2021-09-07 07:46:23
步進電機與步進電機控制器連接:A+:黑A-:綠B+:紅B-:藍電機控制器與arduino板連接:PUL-,DIR-,EN-連arduino的地EN+:脫機信號,接地或者不接DIR+:控制轉動方向,高電平正轉PUL+:控制脈沖...
2021-07-08 07:21:38
特點◆ 高性能、低價格◆ 采用獨特的控制電路,有效的降低了噪音,增加了轉動平穩性◆ 最高反應頻率可達200Kpps ◆ 步進脈沖停止超過100ms時,線圈電流自動減半,減小了許多場合的電機過熱◆ 雙
2008-11-07 16:10:51
的用戶多數不研究電機的控制和優化,而是將其應用于某個場合。基于這點,國外開始盛行一體化步進系統,即將步進電機、反饋裝置、驅動放大器、運動控制器組合成一個整體。其優勢為:體積小、故障率低、無需匹配電機
2021-07-05 06:12:18
01步進電機驅動控制器步進電機驅動器作為實驗裝置可控的部分,能夠提供自動測量的方法。前面已經有兩款步進電機驅動器:SH-20403AXIS12雙軸藍牙移動框架基于ESP8266WiFi步進電機控制
2021-08-31 08:32:52
控制器硬件:一體化步進電機控制器 modbus-rtu-485控制器云臺硬件:北京江云光電 DZY200RA100電動旋轉云臺1,控制接線,連接RS485通信接線: USB轉485的 T/R+-
2021-08-31 08:26:26
SM1P步進電機控制器怎么接線?
2021-10-09 07:33:24
江湖救急呀,大神們。小弟目前的任務是用labview來編寫步進電機控制器程序,也就是編寫脈沖發生器的程序,不知道該如何開始,求大神們給點思路,多指點指點。多謝了。
2015-04-23 14:54:39
伺服電機控制器與步進電機控制器有啥不一樣?
2021-02-25 07:42:10
控制器的輸出信號為雙脈沖,能否控制單脈步進驅動器驅動兩相步進電機?
2023-04-04 16:42:23
用vhdl語言做步進電機的控制器。應該如何入手呢?看了很多資料,各有各的思路,越看越混亂,要分成幾個模塊去做呢? 求大神帶!
2016-04-27 10:21:33
基于LabVIEW的步進電機控制器的設計
2012-09-04 15:14:31
新人一枚,希望大家能發個關于 基于LabVIEW的步進電機PID速度控制器 的文章,謝謝了!!!!
2015-04-20 20:34:47
如何利用HMI USART串口屏做一個步進電機控制器呢?其代碼該怎樣去實現呢?
2021-12-23 06:55:13
本文介紹通過FPGA實現的步進電機控制器。該控制器可以作為單片機或DSP的一個直接數字控制的外設,只需向控制器的控制寄存器和分頻寄存器寫入數據,即可實現對步進電機的控制。
2021-04-29 06:05:44
步進電機控制器能夠發出均勻脈沖信號,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所需要的強電流信號,帶動步進電機運轉。步進電機控制器能夠準確的控制步進電機轉過每一個角度。驅動器所接收
2020-10-05 09:00:33
微型步進電機驅動控制器,北京偉恩斯技術有限公司集驅動和控制于一體,結構緊湊,便于安裝,廣泛運用于生物儀器、醫療器械、工業自動化、多點控制組網矩陣等領域。有脈沖方向型,485總線型,CAN總線型等,通過編程,可在驅動器內部實現軌跡規劃等功能,提高運動控制系統的精度和效率。...
2021-08-31 08:09:29
微型步進電機驅動控制器到底長什么樣?
2021-10-28 07:46:29
微型步進電機驅動控制器,北京偉恩斯技術有限公司集驅動和控制于一體,結構緊湊,便于安裝,廣泛運用于生物儀器、醫療器械、工業自動化、多點控制組網矩陣等領域。有脈沖方向型,485總線型,CAN總線型等,通過編程,可在驅動器內部實現軌跡規劃等功能,提高運動控制系統的精度和效率。...
2021-08-31 07:06:25
國內普遍采用TM320系列的DSP器件作為永磁同步電機控制系統的主控制器,因CPU負載過重導致系統實時性降低的問題日益顯著。采用具有并行工作特性的FPGA器件作為主控制器能夠提高系統實時性。因此,我們具體該怎么設計呢?
2019-08-14 08:02:56
STM32發出脈沖一般有哪幾種方式?怎樣通過控制器輸入脈沖去控制步進電機呢?
2021-12-21 06:25:47
求大神分享SM1P步進電機控制器操作說明
2021-10-09 07:40:22
Arduino 2560控制兩個步進電機用arduino和步進電機控制器驅動兩個步進電機,具體的接線過程和怎樣連接都在圖片上。準備工具:兩個步進電機(我用的是J42):Arduino板(我用
2021-08-31 06:13:29
描述硬盤步進電機速度控制器這個想法來自控制步進電機的需要,而不需要復雜的編程或微控制器和其他復雜的 IC,我想找到最便宜的解決方案。PCB
2022-08-05 06:29:44
跪求!!求基于LabVIEW步進電機PID速度控制器的設計
2015-04-21 15:52:00
基于GAL器件的步進電機控制器的研究與設計
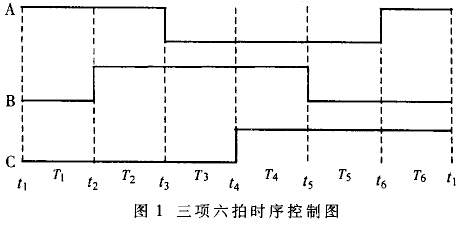
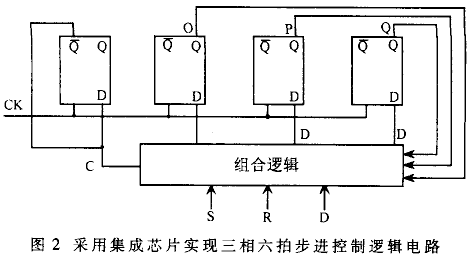
采用GAL控制脈沖分配的邏輯設計若采用集成電路芯片來實現三相六拍步進電機的控制,所用器件較多! 電路一般比較復雜# 為
2008-10-21 01:53:23 42
42 LabVIEW控制步進電機的并口通訊研究:本文給出了基于LabVIEW控制步進電機的方法,并講述了控制系統的構成。
2009-04-02 10:55:13 68
68 本文描述的是常用的單片機和步進電機驅動芯片實現步進電機的控制和驅動。
2009-04-02 15:47:51 89
89 本文利用陳列邏輯器件GAL16V8對步進電機實現控制,給出了89C55單片機控制的硬件、軟件設計實例。
2009-04-02 16:30:16 200
200 本文應用單片機、步進電機驅動芯片、字符型LCD 和鍵盤陣列, 構建了集步進電機控制器和驅動器為一體的步進電機控制系統。二維工作臺作為被控對象通過步進電機驅動滾珠絲桿在X/
2009-04-06 17:12:31 41
41 直流步進電機控制器實例(VHDL源代碼):步進電機控制器.vhd,直流電機控制器.vhd
2009-05-27 08:51:54 62
62 直流步進電機控制器實例(VHDL源代碼):
2009-05-27 10:23:05 47
47 本文應用單片機、步進電機驅動芯片、字符型LCD和鍵盤陣列,構建了集步進電機控制器和驅動器為一體的步進電機控制系統。二維工作臺作為被控對象通過步進電機驅動滾珠絲桿
2009-09-10 09:19:30 33
33 用MCP定時器控制步進電機:步進電機簡介1.1.1 步進電機步進電機和普通電動機不同之處是步進電機接受脈沖信號的控制。步進電機靠一種叫環形分配器的電子開關器件,通過功
2009-09-19 11:36:32 22
22 用GPIO做步進電機控制:步進電機和普通電動機不同之處是步進電機接受脈沖信號的控制。步進電機靠一種叫環形分配器的電子開關器件,通過功率放大器使勵磁繞組按照順序輪流接通
2009-09-19 11:37:58 69
69 GY8608 CAN 總線接口的雙路步進電機控制器:1、CAN 總線接口,可通過同時控制2 路步進電機。2、如果只控制一路步進電機,最大工作頻率25khz。3、如果同時控制兩路步進電機,則
2010-01-14 18:40:14 34
34 控制步進電機的現場總線端子-集成的步進電機控制器:用于新驅動技術的總線端子為最高功率為200W 的小型步進電機提供了運動控制解決方案。KL2531和KL2541 步進電機端子便是用于傳
2010-10-06 09:52:57 41
41 TMC428是TRINAMIC公司最新開發的步進電機運動控制器,它可減少電機控制軟件設計的工作量,降低開發成本。以它為核心(包括TMC236型步進電機驅動器)構成的3軸步進電機驅動
2010-12-03 15:47:29 71
71 基于FPGA的步進電機控制器設計
?????? 目前大多數步進電機控制器需要主控制器發送時鐘信號,并且要至少一個I/O口來輔助控
2010-02-09 10:44:44 2465
2465 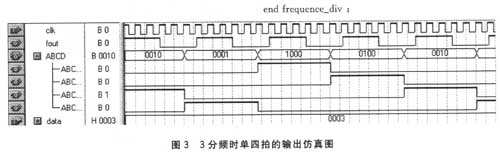
根據Nios II處理器的Avalon總線規范,設計了一款面向步進電機的控制器IP核。該定制IP核采用軟、硬件協同設計的方法,功能符合Avalon總線的讀寫傳輸時序,具有完備的步進電機驅動能力。仿
2011-12-23 14:02:32 44
44 基于單片機的步進電機控制系統的研究....
2016-01-04 15:25:39 23
23 TMC428型3軸步進電機控制器的原理及應用
2016-04-25 10:10:07 28
28 基于最小偏差法的步進電機速度控制方法研究。
2016-05-03 13:52:59 3
3 基于最小偏差法步進電機加減速控制的研究。
2016-05-03 13:52:59 8
8 基于單片機的步進電機升降速控制研究,下來看看
2016-05-03 13:52:59 9
9 基于SOPC的步進電機加減速PWM控制器IP核設計
2016-05-03 13:52:59 18
18 步進電機短位移高響應加減速控制方法研究。
2016-05-04 14:09:56 4
4 步進電機的精確控制方法研究,有需要 下來看看
2016-05-04 14:35:59 8
8 步進電機控制器,感興趣的小伙伴們可以看一看。
2016-08-23 16:23:32 16
16 電子、電子信息專業電路單片機學習教程資料——步進電機的精確控制方法研究
2016-08-26 17:02:46 0
0 步進電機驅動控制技術及其應用設計研究
2016-12-26 17:21:55 0
0 單片機控制步進電機的方法研究與應用
2021-11-30 11:55:58 8
8 現代社會分工日益細化。不論企業還是用戶,只有專注于最擅長的工作才能使利益最大化。步進電機的用戶多數不研究電機的控制和優化,而是將其應用于某個場合。基于這點,國外開始盛行一體化步進系統,即將步進電機
2017-11-01 10:16:01 5
5 的步進電機多軸控制器是以微控制器(MCU)/微處理器(MPU)/專用集成電路(ASIC)/數字信號處理器(DSP)為核心,再輔以其他外圍分立器件構成的。這種結構的步進電機多軸控制器的優點在于其硬件結構清晰,易于復制再現,對于類
2017-11-08 14:21:45 12
12 意法半導體新推出的步進電機控制芯片L6470在一顆芯片上集成了功率級和一個數字控制內核。這款步進電機控制芯片能夠通過SPI接口接收微控制器的運動曲線命令,按照預制的加速度和速度曲線自動執行運動,還能自動加快電機的運轉速度,并使之保持預設的轉速。
2018-07-19 07:07:00 2411
2411 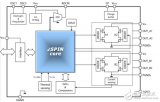
提出一種應用現場可編程門陣列(FPGA)實現多軸步進電機控制器的方法。采用IP設計思想,步進電機的運動控制由硬件電路(步進電機IP核)實現,軌跡計算由同一芯片上的微處理器(Nios II軟核)實現
2017-12-06 10:41:30 23
23 多軸步進電機插補控制器及多軸步進電機運動控制卡控制方法
2018-04-11 10:24:47 26
26 步進電機和伺服電機是工控領域應用最廣泛的兩類產品,而它們的核心分別是步進電機控制器與伺服電機控制器,本文將給大家講解這兩種器件不一樣的地方。
2018-09-16 09:48:19 2770
2770 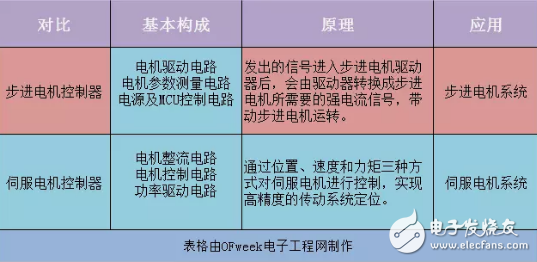
該項目旨在通過制造模塊化控制器來簡化步進電機的使用,該模塊化控制器可以輕松驅動步進電機,而無需使用微控制器來完成工作。
2019-08-08 11:52:03 17706
17706 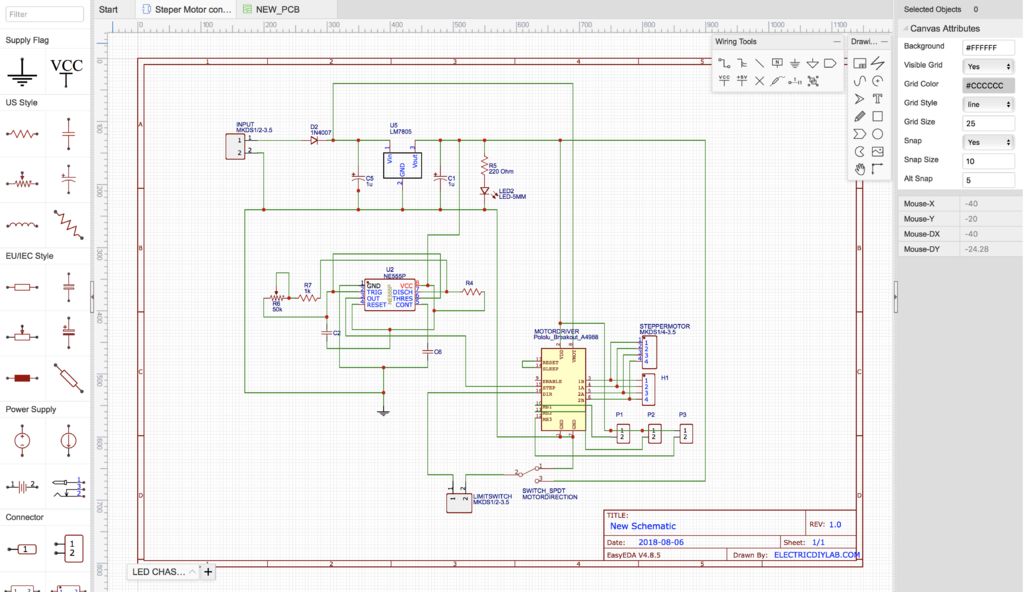
步進電機控制器是一種能夠發出平均脈沖信號的電子產品,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所需要的強電流信號,帶動步進電機運轉。
2019-10-01 15:10:00 5488
5488 
步進電機控制器接線圖如下:接線之前我們需要大概了解,控制器需要發送什么信號,才能控制驅動器,進而操縱電機。
2019-10-01 08:51:00 14742
14742 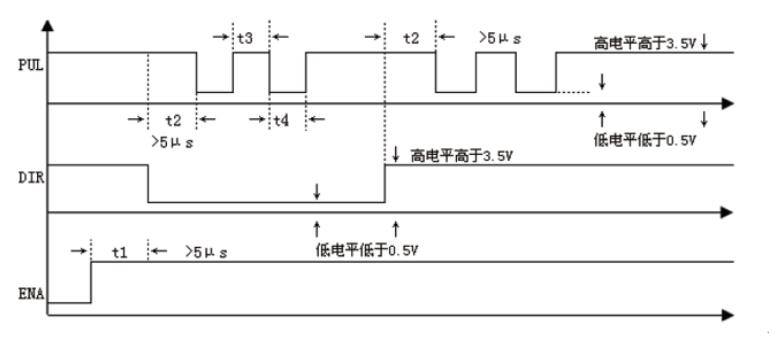
步進電機控制器是一種能夠發出均勻脈沖信號的電子產品,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所需要的強電流信號,帶動步進電機運轉。步進電機控制器能夠準確的控制步進電機轉過每一個角度。
2019-10-01 08:58:00 15865
15865 步進電機控制器:它是一種能夠發出均勻脈沖信號的電子產品,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所需要的強電流信號,帶動步進電機運轉。步進電機控制器能夠準確的控制步進電機轉過每一個角度。
2019-12-10 08:49:06 7858
7858 為了適應這種控制需求,對通用步進電機控制器進行了改進,使其在具有自動和手動控制功能的同時,引入限位信號反饋控制。電機控制器使用硬件描述語言(HDL)編寫,而限位信號則由位置感應電路中的光電開關器件自動反饋。
2020-04-15 10:03:01 1518
1518 
步進電機和伺服電機是工控領域應用最廣泛的兩類產品,而它們的核心分別是步進電機控制器與伺服電機控制器,本文將給大家講解這兩種器件不一樣的地方。
2020-12-14 20:26:09 1309
1309 步進電機和伺服電機是工控領域應用最廣泛的兩類產品,而它們的核心分別是步進電機控制器與伺服電機控制器,本文將給大家講解這兩種器件不一樣的地方。
2021-01-31 06:17:24 15
15 介紹基于FPGA 的步進電機控制器的設計, 在分析步進電機的工作原理的基礎上, 給出了層次化設計方案與VHDL程序,并利用Quartus Ⅱ進行了仿真并給出了仿真結果。它以FP GA 作為核心器件
2021-02-05 11:37:00 27
27 步進電機控制器是一種能夠發出均勻脈沖信號并且運用范圍廣泛的電機控制器,步進電機控制器怎么使用?下面就由小編來簡單介紹一下!
2021-07-19 09:52:57 5456
5456 的發展,步進電機的需求量與日俱增,在各個國民經濟領域都有應用。 步進電機控制系統由步進電機控制器、步進電機驅動器、步進電機三部分組成,步進電機控制器是指揮中心,它發出信號脈沖給步進電機驅動器,而步進電機驅動器把接
2021-07-19 15:49:33 11901
11901 本文檔作備份用。摘 要: 設計了一種具有多模式的步進電機控制裝置,本裝置基于STC的一款單片機STC89C52,軟件部分由C51編寫,包含啟停中斷程序、轉向中斷程序、步進電機調速程序以及鍵盤信號
2021-11-23 16:22:51 18
18 引出MCU是 stm32F407ZGT6 最小系統板根據步進電機控制器的資料可以知道 步進電機的速度和轉過的角度都是通過 PUL + 和PUL- 來控制的(這里...
2021-12-05 12:51:16 0
0 有多種版本的步進電機類型,也有多種版本的步進電機控制器設計。本電路是一款使用ICTDA2030作為驅動器的通用步進電機控制器。
2022-06-04 17:17:00 2478
2478 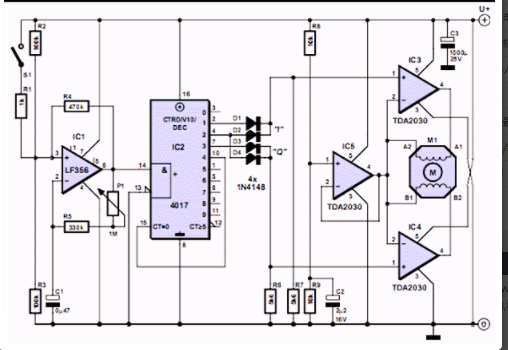
MS35711T 器件是一款步進電機控制器, 它使用外部 N 溝道 MOSFET 來驅動一個雙極步進電機或兩個刷式直流電機。 MS35711T 支持全步進到 1/256 步進驅動模式。通過使用自適應
2022-07-12 09:43:28 3356
3356 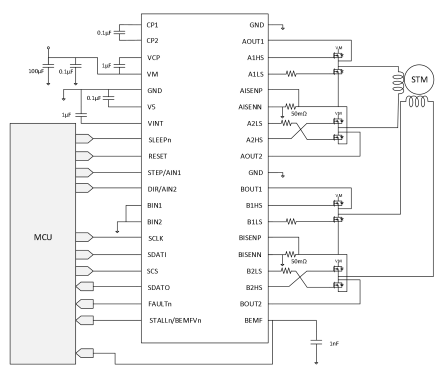
電子發燒友網站提供《硬盤步進電機速度控制器.zip》資料免費下載
2022-07-22 11:29:02 2
2 MS35711T 器件是一款步進電機控制器, 它使用外部 N 溝道 MOSFET 來驅動一個雙極步進電機或兩個刷式直流電機。
2022-07-31 10:26:46 4
4 電子發燒友網站提供《PCB設備步進電機控制器.zip》資料免費下載
2022-08-22 16:17:53 0
0 電子發燒友網站提供《如何測試TB6600步進電機驅動器控制器和步進電機.zip》資料免費下載
2022-12-06 15:51:08 3
3 步進電機控制器是一種能夠發出均勻脈沖信號的電子產品,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所
需要的強電流信號,帶動步進電機運轉。步進電機控制器能夠準確的控制步進電機轉過每一個
2023-03-23 10:24:22 1
1 步進電機控制器是一種專門用于控制步進電機的設備,可以用來控制步進電機的轉速和方向。步進電機控制器通常包括一個驅動電路板和一個控制板,驅動電路板用于提供電源和輸出脈沖信號,控制板則用于控制步進電機的運行。
步進電機控制器的應用設置一般包括以下幾個方面:
2023-03-26 22:30:20 1184
1184 步進電機控制器是一種能夠發出均勻脈沖信號的電子產品,它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機
所需要的強電流信號,帶動步進電機運轉。步進電機控制器能夠準確的控制步進電機轉過每一個
2023-05-05 14:16:03 4
4 電子發燒友網站提供《步進電機控制器的FPGA的實現.pdf》資料免費下載
2023-10-07 16:29:17 1
1 電子發燒友網站提供《基于FPGA的步進電機伺服控制器設計.pdf》資料免費下載
2023-10-25 09:10:40 0
0 控制,需要使用步進電機控制器。步進電機控制器是一種電子裝置,用于接收和處理控制信號,并將其轉換為電機驅動信號。通過調整步進電機控制器的參數設置,可以使電機按照需求進行旋轉,實現精確的運動控制。 在進行步進電
2024-01-19 10:50:22 503
503 步進電機控制器是一種能夠發出均勻脈沖信號的電子產品,主要用于控制步進電機的運動。它發出的信號進入步進電機驅動器后,會由驅動器轉換成步進電機所需要的強電流信號,帶動步進電機運轉。
2024-02-07 17:57:00 651
651 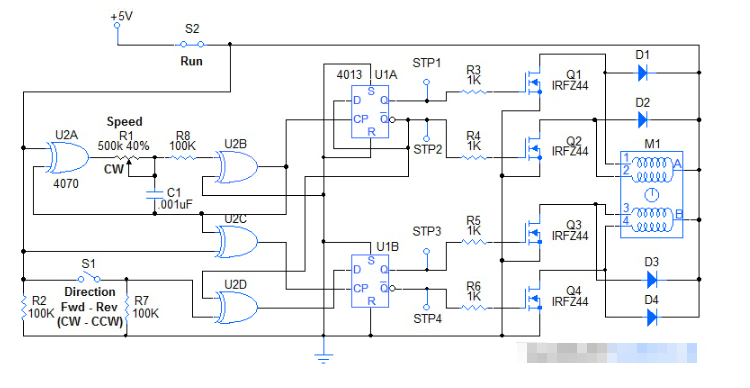
 電子發燒友App
電子發燒友App



































評論