IIR濾波器零相位數字濾波及其應用
摘要: 本文介紹了一種利用Delphi7實現數字濾波器零相位濾波的方法,與一般差分濾波方法相比,該方法不僅可以避免相移,而且還能改善起始部分的波形畸變,這一點在信號處理中具有重要的應用價值。
關鍵詞: 虛擬儀器信號處理零相位數字濾波
Zero?phase Digital Filter and Application
Fan Xinhai??An Gang??Zhang Chuanqing
Abstract: This paper introduces a method to realize zero?phase filtering for digital filters using Delphi7. Comparing with general difference filter, the zero?phase digital filter can not only avoid phase?shifting, but also improve the wave aberration of section start. This method has important practical value in signal processing.
Keywords: virtual instrument, signal processing, zero?phase digital filtering.
0引言
在動態測試信號處理過程中,濾波器是常用的測試儀器之一。它常被用于抗混濾波,以避免傅立葉變換時在頻域產生混疊,或從具有多種頻率成分的復雜信號中,將感興趣的頻率成分提取出來,而將不感興趣的頻率成分衰減掉。在傳統測試儀器中,濾波器的功能通常需要依靠硬件系統來實現。
隨著數字信號處理技術的不斷完善,計算機硬件技術的日新月異以及軟件技術飛速發展,測試儀器系統的設計思想發生了重大改變。部分傳統的專用測試設備會逐步被以計算機和應用軟件為核心的虛擬儀器所代替\[1\]。虛擬儀器的出現標志著“軟件即儀器(The soft is the instrument)”時代的到來。在計算機輔助測試系統(CAT,Computer Aided Test)中,以往模擬濾波器(AF,Analog Filter)的功能,可用數字濾波器(DF,Digital Filter)來替代。數字濾波器的實現不但比模擬濾波器容易的多,而且還能獲得較理想的濾波器性能。
2數字濾波器的時域描述與分類
對于一個線性移不變(LSI,Linear Shift Invariant)離散時間系統,如圖1所示,可用如下差分方程表示:y(n)+∑Nk=1a(k)y(n-k)=∑Mr=0b(r)x(n-r)(1)式中a(k),b(r)為方程系數。
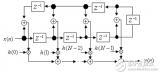
圖1LSI系統
如果a(k),k=1,2,Λ,N不全為零,該系統為無限沖擊響應(IIR)系統。若a(k)均為零,并令b(0)=1,則y(n)=∑Nr=1b(r)x(n-r)+x(n)(2)該系統為有限沖擊響應(FIR)系統。
由此,數字濾波器在從實現方法上,有IIR濾波器和FIR濾波器之分。這兩類濾波器無論在性能上,還是在設計方法上都有著很大的區別。IIR數字濾波器與FIR濾波器相比,前者保留了模擬濾波器的優點,幅頻特性較好,但存在相位失真。后者相頻特性較好,可實現線性相位,但在相同指標要求下要比前者的階數高的多。
3差分數字濾波及其存在的問題
IIR數字濾波器的設計方法主要有雙線性Z變換法和沖激響應不變法;FIR數字濾波器的設計方法主要有窗函數法、頻率抽樣法和切比雪夫逼近法等。有關數字濾波器設計的詳細方法見文獻\[2\],這里就不再贅述。
對于設計好的濾波器,確定出濾波器的系數,通過對差分方程式(1)或式(2)的疊代算法,可以實現IIR濾波器或FIR濾波器的數字濾波。考慮到程序的通用性,這里就按式(1)編寫一個差分濾波函數DiffFilter(b,a,x),調用參數為三個數組,b用于存放濾波器的系數b(r)(r=0,1,…,M);a用于存放濾波器的系數a(k)(k=0,1,…,N),且a(0)=1;x用于存放輸入信號,返回后用于存放濾波后的輸出信號。如果將調用參數a均賦零值,則可實現FIR濾波器的數字濾波。
在此,用一實例進行說明。圖2為某型坦克發動機轉速1000rpm時,在排氣口測得的噪聲信號(采樣點數1024,采樣頻率4KHz)。從信號的波形可以看出,它具有一定的周期性,主要是以發動機周期性排氣產生的噪聲為主。
圖2某型坦克發動機噪聲信號
采用窗函數(Hanning窗)法設計出某200階FIR低通濾波器,截止頻率為200Hz,分析頻率為2KHz,其幅頻曲線及相頻曲線如圖3所示。
圖3低通濾波器的幅頻特性和相頻特性
利用該FIR低通數字濾波器對圖2所示發動機噪聲信號進行差分濾波,濾波后的波形如圖4所示。
圖4差分濾波后的發動機噪聲信號
對比圖3和圖4所示波形可以看出,差分濾波后,信號變得“光滑”了許多,原來的“毛刺”被濾掉了。但同時也可以看出差分濾波方法存在兩個問題:一是濾波后的信號相對與原信號而言,發生了相移;二是濾波后的信號在起始部分,波形畸變較為嚴重。在信號處理中,如果對信號的相位有特殊的要求,相移問題需要引起高度的注意。而起始部分的畸變是由于疊代過程中,沒有考慮濾波器的初始條件,剛開始點數少,沒能用到濾波器全部系數的緣故。大多情況下,這種畸變可以接受,但當數據較短,而濾波器的階數又較高時,這種畸變會帶來較大的負面影響。
如果輸入信號為一單位脈沖信號,即
x(n)=1,n=1
0,n≠1
那么,濾波器的輸出為其脈沖響應。本文所用200階FIR低通數字濾波器的脈沖響應如圖5所示。
圖5濾波器的脈沖響應3零相位數字濾波算法及其實現
3.1零相位數字濾波的算法
為了克服差分數字濾波中存在的上述兩個問題,可以采用一種零相位濾波的方法,該方法的基本思路是:先確定出濾波器的初始條件,然后將原序列的首尾進行擴展,把擴展后序列通過濾波器,將所得結果反轉后再次通過濾波器,最后將所得結果再反轉,并去掉首尾的擴展部分,即可得到零相位濾波后的輸出序列\[3\]。本文采用四次差分濾波方式給出一種便于實現的詳細算法,假設輸入信號為x(n),n=0,1,…,P。
(1) 編寫差分濾波函數DiffFilter(b,a,x),調用參數如前所述。
(2) 對于IIR濾波器通常有M=N,求濾波器的初始條件e(q),q=0,1,…,N-1,這里記E=[e(0),e(1),…,e(N-1)]T,則有
E=1+a(1)1-1…0
a(2)01…0
MMMOM
a(N)00…-11× b(1)-b(0)a(0)
b(2)-b(0)a(1)
M
b(Nn)-b(0)a(N)(3)
(3) 對原輸入序列x(n)的首尾進行擴展,在x(n)的前面添加3N個數,在后面添加3N個數,擴展后的序列記為x′(n),n=0,1,…,P+6N。
x′(n)=2x(0)-x(3N-n)
x(n-3N)
2x(P)-x(P-1-(n-P-3N-n))
n<3N
3N?n<P+3N
P+3N?n?P+6N(4)
(4) 進行正向濾波:先用b,a和x′(n)調用DiffFilter(b,a,x)函數,計算x′(n)通過
H(z)=∑Mm=0b(m)z-m/(1+∑Mm=1a(m)z-m)(5)
的輸出y′(n),然后生成一長度為P+6N+1的單位脈沖信號h(n),用z,a和h(n)調用DiffFilter(b,a,x)函數,計算h(n)通過
H(z)=∑M-1m=0y′(0)e(m)z-m/(1+∑Mm=1a(m)z-m)(6)
的輸出y′(n),并記y(n)=y′(n)+y″(n)。
(5) 進行反向濾波:將正向濾波結果反轉,記x′(n)=y(P+6N-n),重復步驟4°,得到反向濾波后的結果。
(6) 將反向濾波的結果反轉,并刪除首尾的擴展部分,即可得到最后的濾波結果。
3.2零相位數字濾波的實現
Borland公司推出的Delphi編程語言,具有合理的單元化結構、優化的編譯環境,開發速度快、編程效率高。在實現同樣功能的情況下與其它語言相比,不僅編寫的代碼量少、程序可移植性強,而且還有許多優秀的組件包可供使用。最為方便的是可以使用動態數組,隨時能夠改變數組的長度,這一點非常適合數字信號處理。
作者利用Delphi7編寫了利用雙線性Z變換法設計Butterworth型IIR濾波器和利用窗函數法設計FIR濾波器,以及差分數字濾波算法和零相位數字濾波算法應用程序,并作為集成測試軟件平臺的一個虛擬儀器。其中零相位數字濾波算法程序設計流程如圖6所示。
圖6零相位數字濾波算法的流程圖
圖7所示為圖2所示信號零相位數字濾波后的波形,通過與原信號(圖2)和差分濾波后的信號(圖4)對比不難看出:零相位數字濾波后的輸出與原信號中的相位基本一致,并且起始部分沒有畸變。但不可否認,零相位數字濾波算法相對于普通差分濾波算法計算量要大許多,但以目前計算機的運算能力,計算量稍大并不是什么主要問題。
? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ? 圖7零相位濾波后的波形
4結束語
本文介紹了一種利用四次差分濾波算法,實現零相位數字濾波的方法,并利用Delphi7編寫了應用軟件。通過與普通差分濾波器的實例對比分析,說明零相位數字濾波不僅能夠避免相移,而且還能改善差分濾波起始部分的波形畸變。這一點在數字信號處理中具有重要的應用價值。
參考文獻
\[1\] 程 虎. 虛擬儀器的現狀和發展趨勢.現代科學儀器,1999(4):6~9
\[2\] 胡廣書編.數字信號處理—理論、算法與實現.清華大學出版社,1997
\[3\] 紀躍波,秦樹人,湯寶平.零相位數字濾波器.重慶大學學報,2000.23(6):4
IIR濾波器零相位數字濾波及其應用
- 濾波器(174522)
相關推薦
基于FPGA和MATLAB實現IIR數字濾波器的設計和仿真驗證分析
IIR數字濾波器在很多領域中都有著廣闊的應用。與FIR數字濾波器相比,IIR數字濾波器可以用較低的階數獲得較高的選擇性,而且所用存儲單元少,經濟效率高。一個N階IIR數字濾波器的系統函數為:
2020-07-23 17:05:08 2191
2191
 2191
2191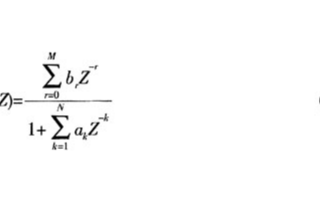
IIR濾波器和FIR濾波器的對比分析介紹
1.兩種濾波器都是數字濾波器。根據沖激響應的不同,將數字濾波器分為有限沖激響應(FIR)濾波器和無限沖激響應(IIR)濾波器。對于FIR濾波器,沖激響應在有限時間內衰減為零,其輸出僅取決于當前和過去
2019-06-26 06:15:35
iir濾波器相位校正
iir濾波器后面級聯一個全通濾波器進行相位校正,不知道怎樣設計一個全通濾波器,以及不會用函數把兩個濾波器級聯起來,望大神指導、、、、{:4:}
2013-06-09 15:20:23
數字濾波器-IIR濾波器原理介紹&Verilog HDL設計
本文將簡單介紹另一種數字濾波器——IIR濾波器的原理,詳細介紹使用Verilog HDL設計直接型IIR濾波器的方法。數字濾波器數字濾波器從實現結構上劃分,有FIR和IIR兩種。FIR的特點是:線性相位
2020-09-27 09:22:58
數字濾波器是什么
特點,它不僅能完成模擬處理的大部分功能,滿足濾波器對幅度和相位特性的嚴格要求,而且還能避免模擬濾波器所無法克服的電壓漂移,溫度漂移和噪聲等問題,模擬處理由于成本可靠性等原因而無法實現的功能。數字濾波
2021-07-28 08:37:12
數字濾波器的分類
本帖最后由 武漢購線網 于 2017-11-10 16:51 編輯
數字濾波器的分類:數字濾波器http://www.gooxian.com/product_detail-9722.htm
2017-11-10 16:41:59
數字濾波器的分類
數字濾波器的分類:數字濾波器的種類很多,分類方法也不同,可以從功能上分,也可以從實現方法上分,還可以從設計方法上來分等。一種比較通用的分類方法是將數字濾波器分為兩大類,即經典濾波器和現代濾波器。經典
2017-05-25 09:27:52
零基礎學FPGA(三十) IIR數字濾波器的FPGA實現筆記
濾波器就不能保證線性相位以及穩定性問題。下面是就算是我做的一個IIR的筆記吧,最近也看了不少這方面的資料,算是做一個整理。一、關于IIR數字濾波器當然關于IIR濾波器的知識,想必大家在教材上都已經很熟
2015-07-26 21:44:21
FIR數字濾波器的三種設計方法
,只能通過改變零點位置來改變性能,為了達到高的選擇性必須用較高的階數。對于同樣的濾波器設計指標,FIR濾波器要求的階數可能比 IIR濾波器高10倍以上。由于 FIR 數字濾波器具有嚴格的相位特性,對于
2021-08-08 07:00:00
 電子發燒友App
電子發燒友App










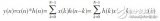
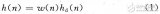

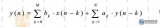
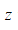












評論