BP神經(jīng)網(wǎng)絡(luò)圖像壓縮算法乘累加單元的FPGA設(shè)計(jì)
0 引 言
??? 神經(jīng)網(wǎng)絡(luò)(Neural Networks)是人工神經(jīng)網(wǎng)絡(luò)(Ar-tificial Neural Networks)的簡(jiǎn)稱,是當(dāng)前的研究熱點(diǎn)之一。人腦在接受視覺(jué)感官傳來(lái)的大量圖像信息后,能迅速做出反應(yīng),并能在腦海中重現(xiàn)這些圖像信息,這不僅與人腦的海量信息存儲(chǔ)能力有關(guān),還與人腦的信息處理能力,包括數(shù)據(jù)壓縮能力有關(guān)。在各種神經(jīng)網(wǎng)絡(luò)中,多層前饋神經(jīng)網(wǎng)絡(luò)具有很強(qiáng)的信息處理能力,由于其采用BP算法,因此也稱為BP神經(jīng)網(wǎng)絡(luò)。采用BP神經(jīng)網(wǎng)絡(luò)模型能完成圖像數(shù)據(jù)的壓縮處理。在圖像壓縮中,神經(jīng)網(wǎng)絡(luò)的處理優(yōu)勢(shì)在于:巨量并行性;信息處理和存儲(chǔ)單元結(jié)合在一起;自組織自學(xué)習(xí)功能。
??? 與傳統(tǒng)的數(shù)字信號(hào)處理器DSP(Digital Signal Processor)相比,現(xiàn)場(chǎng)可編程門陣列(Field Programma-ble Gate Array,F(xiàn)PGA)在神經(jīng)網(wǎng)絡(luò)的實(shí)現(xiàn)上更具優(yōu)勢(shì)。DSP處理器在處理時(shí)采用指令順序執(zhí)行的方式,而且其數(shù)據(jù)位寬是固定的,因而資源的利用率不高,限制了處理器的數(shù)據(jù)吞吐量,還需要較大的存儲(chǔ)空間。FPGA處理數(shù)據(jù)的方式是基于硬件的并行處理方式,即一個(gè)時(shí)鐘周期內(nèi)可并行完成多次運(yùn)算,特別適合于神經(jīng)網(wǎng)絡(luò)的并行特點(diǎn),而且它還可以根據(jù)設(shè)計(jì)要求配置硬件結(jié)構(gòu),例如根據(jù)實(shí)際需要,可靈活設(shè)計(jì)數(shù)據(jù)的位寬等。隨著數(shù)字集成電路技術(shù)的飛速發(fā)展,F(xiàn)PGA芯片的處理能力得到了極大的提升,已經(jīng)完全可以承擔(dān)神經(jīng)網(wǎng)絡(luò)數(shù)據(jù)壓縮處理的運(yùn)算量和數(shù)據(jù)吞吐量。圖像壓縮是信息傳輸和存儲(chǔ)系統(tǒng)的關(guān)鍵技術(shù),然而如何進(jìn)行FPGA設(shè)計(jì),以實(shí)現(xiàn)給定的功能已經(jīng)成為神經(jīng)網(wǎng)絡(luò)應(yīng)用的關(guān)鍵。
??? 基于以上原因,選擇FPGA作為三層BP神經(jīng)網(wǎng)絡(luò)圖像壓縮算法的實(shí)現(xiàn)方式,提出了具體的一種實(shí)現(xiàn)方案,并對(duì)其中的重點(diǎn)單元進(jìn)行了FPGA設(shè)計(jì)與仿真驗(yàn)證。
1 BP神經(jīng)網(wǎng)絡(luò)圖像壓縮算法
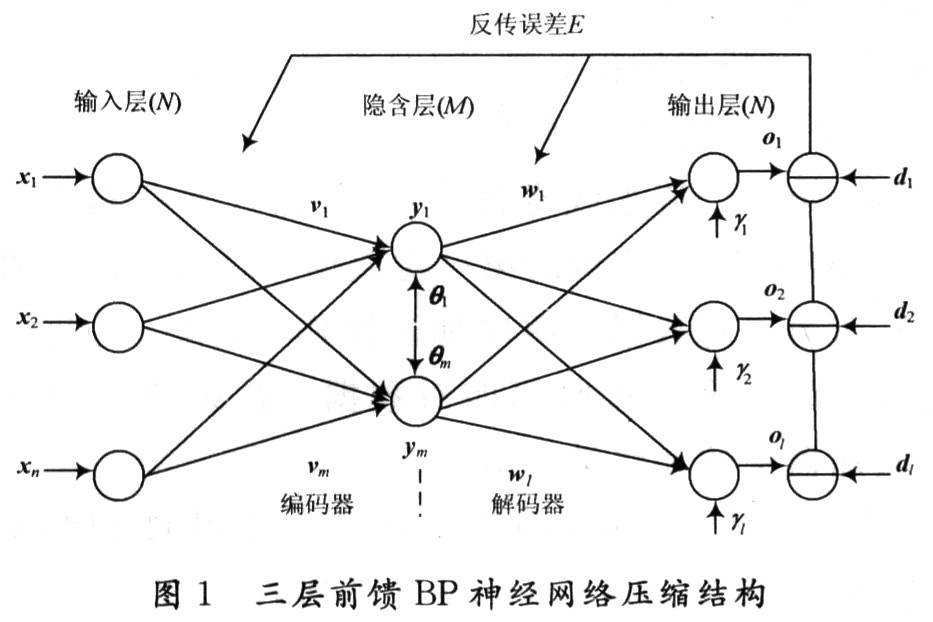
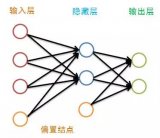
??? 一般習(xí)慣將單隱層前饋網(wǎng)稱為三層前饋網(wǎng),它包括輸入層、隱含層和輸出層。三層BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示,原始數(shù)據(jù)節(jié)點(diǎn)和重建數(shù)據(jù)節(jié)點(diǎn)構(gòu)成節(jié)點(diǎn)數(shù)較大的外層(輸入層和輸出層),而中間的具有較小節(jié)點(diǎn)數(shù)的細(xì)腰層即構(gòu)成壓縮結(jié)果。其基本思想是強(qiáng)迫原始數(shù)據(jù)通過(guò)細(xì)腰型網(wǎng)絡(luò)瓶頸,并期望在網(wǎng)絡(luò)的瓶頸處能獲得較為緊湊的數(shù)據(jù)表示,以達(dá)到壓縮的目的。在網(wǎng)絡(luò)的學(xué)習(xí)過(guò)程中,通過(guò)BP訓(xùn)練算法,調(diào)整網(wǎng)絡(luò)的權(quán)重,使重建圖像在均方誤差意義上盡可能近似于訓(xùn)練圖像。經(jīng)過(guò)訓(xùn)練的網(wǎng)絡(luò)即可用來(lái)執(zhí)行數(shù)據(jù)壓縮任務(wù),網(wǎng)絡(luò)輸入層與隱含層之間的加權(quán)值相當(dāng)于一個(gè)編碼器,隱含層與輸出層之間的加權(quán)相當(dāng)于一個(gè)解碼器。從輸入端輸入的原始圖像數(shù)據(jù)經(jīng)過(guò)神經(jīng)網(wǎng)絡(luò)的處理,在隱含層得到的輸出數(shù)據(jù)就是原始圖像的壓縮編碼,而輸出層矢量即為解壓后重建的圖像數(shù)據(jù)。
??? BP神經(jīng)網(wǎng)絡(luò)用于圖像編碼的壓縮比與輸入層和隱含層的節(jié)點(diǎn)數(shù)有關(guān):
??? 壓縮比一輸入層節(jié)點(diǎn)數(shù)(n)/隱含層節(jié)點(diǎn)數(shù)(m)
??? 因此一般來(lái)說(shuō)采用不同數(shù)目的隱含層神經(jīng)元就可實(shí)現(xiàn)同一圖像的不同壓縮比。
??? 三層BP前饋網(wǎng)中輸入向量X=x(x1,x2,…,xi,…,xn)T,隱含層輸出向量Y=y(y1,y2,…,yi,…,ym)T,輸出層輸出向量O=O(O1,O2,…,Ok,…,Ol)T,期望輸出向量d=d(d1,d2,…,dk,…,dl)T,輸入層到隱含層的權(quán)值向量V=v(v1,v2,…,vj,…,vm)T,其中vj為隱含層第j個(gè)神經(jīng)元對(duì)應(yīng)的權(quán)值向量;隱含層到輸出層的權(quán)值向量W=W(w1,w2,…,wk,…wl)T,其中wk為輸出層第k個(gè)神經(jīng)元對(duì)應(yīng)的權(quán)值向量;隱含層的閾值向量θ=(θ1,θ2,…,θi,…,θm)T;輸出層的閾值向量γ=(γ1,γ2,…,γk,…,γl)T。
?(1)用小的隨機(jī)數(shù)對(duì)每一層的權(quán)值和偏差初始化,以保證網(wǎng)絡(luò)不被大的加權(quán)輸入飽和,并進(jìn)行以下參數(shù)的設(shè)定或初始化:期望誤差最小值;最大循環(huán)次數(shù);修正權(quán)值的學(xué)習(xí)速率;
??? (2)將原始圖像分為4×4或8×8大小的塊,選取其中一塊的像素值作為訓(xùn)練樣本接入到輸入層,計(jì)算各層輸出:
??? 其中:f(·)為BP網(wǎng)絡(luò)中各層的傳輸函數(shù)。
??? (3)計(jì)算網(wǎng)絡(luò)輸出與期望輸出之間的誤差,判斷是否小于期望誤差,是則訓(xùn)練結(jié)束,否則至下一步,其中反傳誤差的計(jì)算式為:
??? 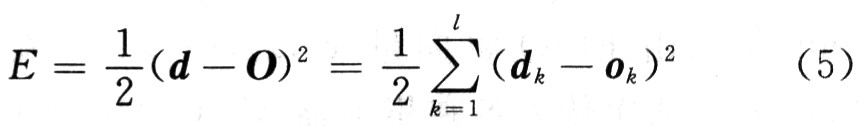
??? (4)計(jì)算各層誤差反傳信號(hào);
??? (5)調(diào)整各層權(quán)值和閾值;
??? (6)檢查是否對(duì)所有樣本完成一次訓(xùn)練,是則返回步驟(2),否則至步驟(7);
??? (7)檢查網(wǎng)絡(luò)是否達(dá)到最大循環(huán)次數(shù),是則訓(xùn)練結(jié)束,否則返回步驟(2)。
??? 經(jīng)過(guò)多次訓(xùn)練,最后找出最好的一組權(quán)值和閾值,組成三層前饋神經(jīng)網(wǎng)絡(luò),用于該算法的FPGA設(shè)計(jì)。
??? 其中,在數(shù)據(jù)預(yù)處理部分,首先將原始圖像分成n×n的小塊,以每一小塊為單位進(jìn)行歸一化。歸一化的目的,主要有以下兩點(diǎn):
??? (1)BP網(wǎng)絡(luò)的神經(jīng)元均采用Sigmoid轉(zhuǎn)移函數(shù),變換后可防止因凈輸入的絕對(duì)值過(guò)大而使神經(jīng)元輸出飽和,繼而使權(quán)值調(diào)整進(jìn)入誤差曲面的平坦區(qū);
??? (2)Sigmoid轉(zhuǎn)移函數(shù)的輸出在-1~+1之間,作為信號(hào)的輸出數(shù)據(jù)如不進(jìn)行變換處理,勢(shì)必使數(shù)值大的輸出分量絕對(duì)誤差大,數(shù)值小的輸出分量絕對(duì)誤差小。網(wǎng)絡(luò)訓(xùn)練時(shí)只針對(duì)輸出的總誤差調(diào)整權(quán)值,其結(jié)果是在總誤差中占份額小的輸出分量相對(duì)誤差較大,對(duì)輸出量進(jìn)行尺度變化后這個(gè)問(wèn)題可迎刃而解。
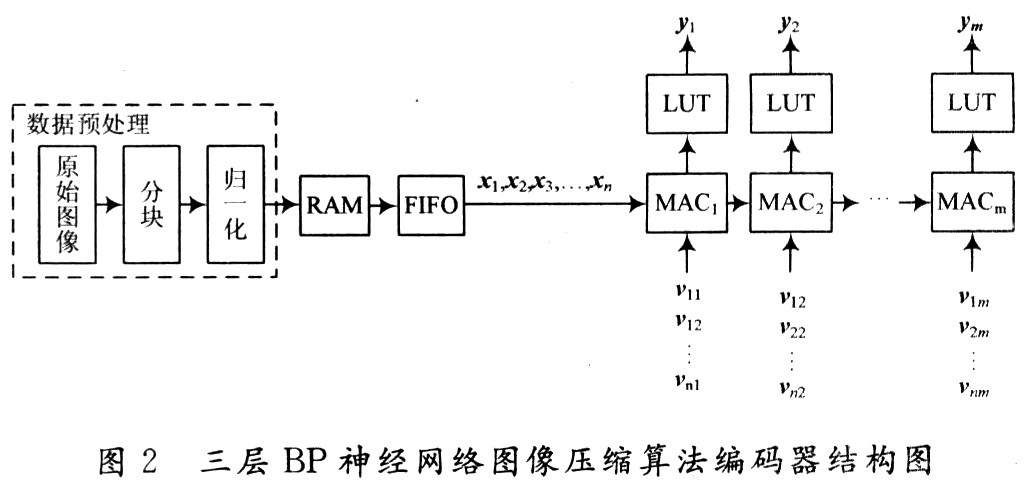
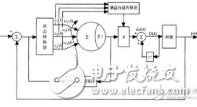
??? 歸一化后得到以每小塊的灰度值為列向量組成的待壓縮矩陣,將該矩陣存儲(chǔ)在RAM里,然后以每一列為單位發(fā)送給先人先出寄存器FIFO(First Input FirstOutput);由FIFO將向量x1,x2,…,xn以流水(pipe-line)方式依次傳人各乘累加器MAC(Multiply-Accu-mulate),相乘累加求和后,送入LUT(Lookup Table)得到隱層相應(yīng)的節(jié)點(diǎn)值,這里L(fēng)UT是實(shí)現(xiàn)Sigmoid函數(shù)及其導(dǎo)函數(shù)的映射。
??? 在整個(gè)電路的設(shè)計(jì)中,采用IP(Intellectual Prop-erty)核及VHDL代碼相結(jié)合的設(shè)計(jì)方法,可重載IP軟核,具有通用性好,便于移植等優(yōu)點(diǎn),但很多是收費(fèi)的,比如說(shuō)一個(gè)高性能流水線設(shè)計(jì)的MAC軟核,所以基于成本考慮,使用VHDL語(yǔ)言完成MAC模塊的設(shè)計(jì),而RAM和FIFO模塊則采用免費(fèi)的可重載IP軟核,使整個(gè)系統(tǒng)的設(shè)計(jì)達(dá)到最佳性價(jià)比。在壓縮算法的實(shí)現(xiàn)中,乘累加單元是共同部分,也是編碼和譯碼器FPGA實(shí)現(xiàn)的關(guān)鍵。
2.2 乘累加器MAC的流水線設(shè)計(jì)及其仿真
??? 流水線設(shè)計(jì)是指將組合邏輯延時(shí)路徑系統(tǒng)地分割,并在各個(gè)部分(分級(jí))之間插人寄存器暫存中間數(shù)據(jù)的方法。流水線縮短了在一個(gè)時(shí)鐘周期內(nèi)信號(hào)通過(guò)的組合邏輯電路延時(shí)路徑長(zhǎng)度,從而提高時(shí)鐘頻率。對(duì)于同步電路,其速度指同步電路時(shí)鐘的頻率。同步時(shí)鐘愈快,電路處理數(shù)據(jù)的時(shí)間間隔越短,電路在單位時(shí)間內(nèi)處理的數(shù)據(jù)量就愈大,即電路的吞吐量就越大。理論而言,采用流水線技術(shù)能夠提高同步電路的運(yùn)行速度。MAC電路是實(shí)現(xiàn)BP神經(jīng)網(wǎng)絡(luò)的重要組成部分,在許多數(shù)字信號(hào)處理領(lǐng)域也有著廣泛應(yīng)用,比如數(shù)字解調(diào)器、數(shù)字濾波器和均衡器,所以如何提高M(jìn)AC的效率和運(yùn)算速度具有極高的使用價(jià)值。本方案采用的MAC設(shè)計(jì)以四輸入為例。
??? 四輸入的MAC電路必須執(zhí)行四次乘法操作和兩次加法操作,以及最后的兩次累加操作。如果按照非流水線設(shè)計(jì),完成一次對(duì)輸入的處理,需要這三步延遲時(shí)間的總和,這會(huì)降低一個(gè)高性能系統(tǒng)的效率。而采用流水線設(shè)計(jì),則可以避免這種延遲,將MAC的操作安排的像一條裝配線一樣,也就是說(shuō),通過(guò)這種設(shè)計(jì)它可以使系統(tǒng)執(zhí)行的時(shí)鐘周期減小到流水線中最慢步驟所需的操作時(shí)間,而不是各步驟延遲時(shí)間之和,如圖3所示。
??? 在第一個(gè)時(shí)鐘邊沿,第一對(duì)數(shù)據(jù)被存儲(chǔ)在輸入寄存器中。在第一個(gè)時(shí)鐘周期,乘法器對(duì)第一對(duì)數(shù)據(jù)進(jìn)行乘法運(yùn)算,同時(shí)系統(tǒng)為下一對(duì)數(shù)據(jù)的輸入作準(zhǔn)備。在第二個(gè)時(shí)鐘邊沿,第一對(duì)數(shù)據(jù)的積存儲(chǔ)在第一個(gè)流水線寄存器,且第二對(duì)數(shù)據(jù)已經(jīng)進(jìn)入輸入寄存器。在第二個(gè)時(shí)鐘周期,完成對(duì)第一對(duì)數(shù)據(jù)積的兩次加法操作,而乘法器完成第二對(duì)數(shù)據(jù)的積運(yùn)算,同時(shí)準(zhǔn)備接收第三隊(duì)數(shù)據(jù)。在第三個(gè)時(shí)鐘邊沿,這些數(shù)據(jù)分別存放在第二個(gè)流水線寄存器,第一個(gè)流水線寄存器,以及輸入寄存器中。在第三個(gè)時(shí)鐘周期,完成對(duì)第一對(duì)數(shù)據(jù)和之前數(shù)據(jù)的累加求和,對(duì)第二對(duì)數(shù)據(jù)的兩次加法操作,對(duì)第一對(duì)數(shù)據(jù)的乘法運(yùn)算,并準(zhǔn)備接收第四對(duì)數(shù)據(jù)。在第四個(gè)始終邊沿,累加器中的和將被更新。
在本設(shè)計(jì)方案中,測(cè)試仿真平臺(tái)選用的FPGA芯片為ALTERA公司CycloneⅡ系列的EP2C8芯片,它采用90 nm的制造工藝,擁有8 256個(gè)邏輯單元,36個(gè)M4K隨機(jī)只讀存儲(chǔ)器,2個(gè)數(shù)字鎖相環(huán),以及18個(gè)硬乘法器等豐富資源。仿真工具使用業(yè)界流行的MentorGraphics公司的仿真軟件Modelsim 6.1f。對(duì)設(shè)計(jì)進(jìn)行驗(yàn)證時(shí),常見(jiàn)的方法是在模擬時(shí)施加輸入激勵(lì)信號(hào),然后“讀”該設(shè)計(jì)的輸出信號(hào),它的主要缺點(diǎn)是隨著模擬器的不同而不同。為了克服此缺點(diǎn),采用的測(cè)試方法是用VHDL編寫(xiě)一個(gè)測(cè)試模型發(fā)生器,稱為Testbench,它的優(yōu)點(diǎn)是通用性好,靈活性強(qiáng),可以隨時(shí)更改輸入激勵(lì),已得到不同的仿真結(jié)果。在對(duì)該MAC模塊進(jìn)行測(cè)試的過(guò)程中,涉及輸入數(shù)據(jù)的轉(zhuǎn)化問(wèn)題,如前所述,在本神經(jīng)網(wǎng)絡(luò)中,輸入數(shù)據(jù)歸一化后,集中在-1~+1之間,所以處理時(shí)必須進(jìn)行轉(zhuǎn)化,最后采用16位補(bǔ)碼形式的定點(diǎn)二進(jìn)制表示法,由于在求和中可能會(huì)產(chǎn)生溢出,還必須包含一個(gè)溢l出狀態(tài)信號(hào)。輸入數(shù)據(jù)轉(zhuǎn)換16位補(bǔ)碼的仿真波形如圖4所示。
?
??? 16位補(bǔ)碼轉(zhuǎn)換原輸入實(shí)數(shù)的仿真波形如圖5所示。
??? 在完成了對(duì)輸入、輸出數(shù)據(jù)的轉(zhuǎn)換之后,編寫(xiě)Testbench(測(cè)試臺(tái))程序,對(duì)基于流水線設(shè)計(jì)的四輸入MAC進(jìn)行行為級(jí)仿真,仿真波形如圖6所示。
??? 綜上所述,在基于流水線的乘法設(shè)計(jì)中,雖然每一步操作后都加入了寄存器,消耗了更多的資源,但卻可以將系統(tǒng)延時(shí)降低到最慢步驟所需要的時(shí)間,極大地提高了同步電路的運(yùn)算速度。
3 結(jié) 語(yǔ)
??? 介紹了基于三層前饋BP神經(jīng)網(wǎng)絡(luò)的圖像壓縮算法,提出了基于FPGA的實(shí)現(xiàn)驗(yàn)證方案,詳細(xì)討論了實(shí)現(xiàn)該壓縮網(wǎng)絡(luò)組成的重要模塊MAC電路的流水線設(shè)計(jì)。在對(duì)BP神經(jīng)網(wǎng)絡(luò)的電路設(shè)計(jì)中,對(duì)傳輸函數(shù)及其導(dǎo)函數(shù)的線性逼近也是近來(lái)研究的熱點(diǎn)之一,本文使用的壓縮查找表雖然能夠滿足設(shè)計(jì)要求,但仍然消耗了大量資源。該研究結(jié)果對(duì)整個(gè)壓縮解壓縮算法的實(shí)現(xiàn)以及多層神經(jīng)網(wǎng)絡(luò)的相關(guān)研究工作提供了參考。
 電子發(fā)燒友App
電子發(fā)燒友App






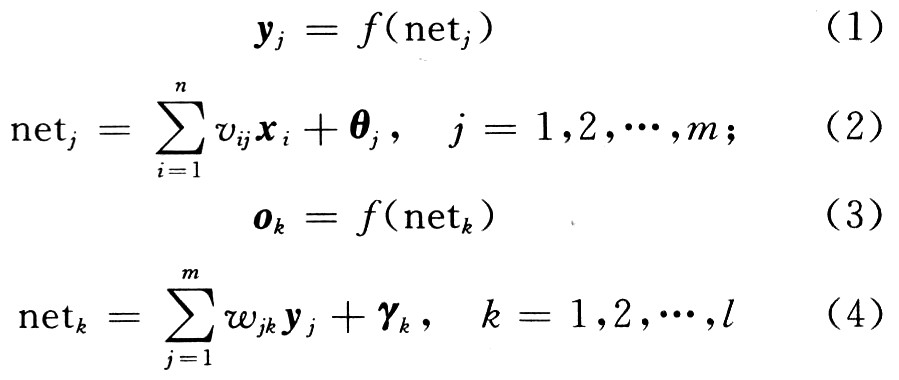







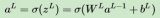










評(píng)論