在占用極低資源的情況下輕松創建適合在DSP48E1Slice或邏輯中實現的高階多相IIR濾波器。
設計人員常常為自己的應用選擇有限脈沖響應(FIR)濾波器,因為此類濾波器易于理解掌握且得到出色的設計與IP實現工具的支持。賽靈思FIR編譯器是一種用于將MATLAB?生成的系數映射到DSP和FPGA邏輯資源中的理想工具。不過在大幅降低FPGA資源占用的情況下設計出能夠滿足特定濾波規范要求的無限脈沖響應(IIR)濾波器是可行的。選用IIR濾波器的主要弊端就是使用設計工具時需要掌握一些專業知識,通常后續還需要手動編寫RTL代碼。不過只要您完成濾波器的架構設計并以定點方式表達出來,利用像賽靈思System Generator這樣的新型工具就能自動為您生成HDL。賽靈思的一篇相關白皮書中全面介紹了各種傳統IIR濾波器[1]。
現在我們來了解一下如何在占用極低FPGA資源的情況下實現高性能多相IIR濾波器。這些濾波器結構特點在于NK+1階的濾波器僅用K次相乘就能實現。此類濾波器對系數量化敏感度低,故可有效地以定點方式實現。此外濾波器級上任何節點的最大增益都是有界的,即中間計算只需要1位余量。這里我們提供的是一種通用架構,適合于實現流水線化并映射到賽靈思7系列器件中的DSP48E1Slice中。該架構包括一定數量的無乘法器五階橢圓濾波器設計,適合在少量FPGA邏輯片中高效完成多相插值和抽取處理。
MATLAB能夠將IIR濾波器設計分解成較低階級聯。這種較低階級聯與直接實現高階差分方程的做法相比,擁有更加理想的數值特性。一般來說低階濾波器選用的是二階雙象限段(SOS),其采用的是直接型1結構。每個SOS需要完成四次相乘、三次相加和部分舍入,以減少進入級聯中用于下一個濾波器的位寬。對于定點實現一般還需要增加一個乘法器來實現段間縮放。
不過級聯分解法對插值器或者抽取器來說并非是一種有效的架構,因為它沒有發揮多相分解的作用。例如在插值過程中,在將輸入數據應用到濾波器之前,需要先在樣本之間插入N-1個零,實現輸入數據上采樣并將輸入采樣率提高到與輸出采樣率相等。但級聯IIR濾波器由于每個SOS內存在的反饋路徑,就無法通過插入零來降低計算量。
用于多相分解的IIR濾波器
本文介紹的濾波器采用圖1中所示的并聯濾波器分解架構。在并聯方式下,每個分支上的濾波器依次比上一分支多延遲1。此外每個分支中的濾波器限制為N帶。每個分支的延遲數由輸入/輸出采樣率決定,但每個An(zN)濾波器的項只涉及z-N冪數,就是說差分方程式只對每第N個輸入/輸出樣本進行計算,而對之間的全部樣本忽略不計。
傳輸函數為被延遲的N帶全通濾波器An(zN)之和。即:
此外還可以把每一個全通濾波器表達為基本全通段的級聯,如圖1所示。設全通段的總段數為K,則H(z)的階數為NK+1。即有:
圖1:上面是IIR濾波器的并聯形式;下面是由級聯的基本濾波器組成的每個分支。
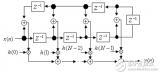
圖2是在直接型1中實現的基本全通段。它由兩個N-樣本延遲元和一個單系數乘法器組成。除了便于使用標準的乘法器,使用直接型1還有其他優勢。它能夠高效地映射到DSPSlice中并在級聯條件下共享延遲資源。
圖2:基本全通段
插值和抽取
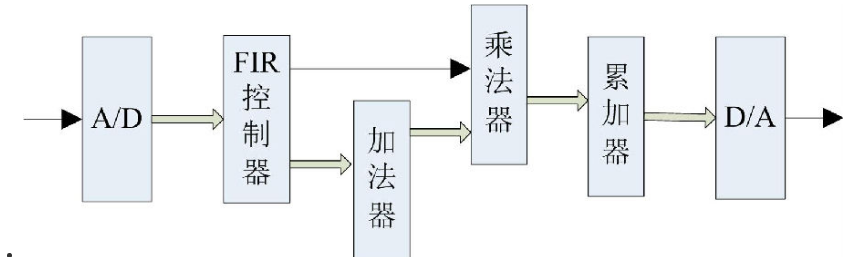
這種濾波器架構可以自然地映射為圖3所示的抽取和插值結構中。這里用換向開關在更高采樣率下切換到每個樣本,取代了圖1中所采用的延遲元。
對隔N插值和抽取的操作,我們既可以圍繞圖3提供的理想結構開展設計,也可以設計由質因數采樣率轉換組成的級聯。分解為質因數[2]可以簡化系數優化問題,因為自由變量的數量較少,且得到的濾波器級聯十分接近理想狀態。在許多應用中,需要的采樣率轉換為2的冪,可通過反復隔2插值或抽取來實現。為不失普遍性,我們先來驗證N=2時的特例。
根據圖3所示,N=2時低通濾波器總階數為5,雖然它由兩個二階全通段和一個延遲元組成。現在應該明確的是,與使用SOS實現該五階IIR濾波器所需的十個乘法器和八個加法器相比,在理想情況下本例只需要兩個乘法器和五個加法器。如果考慮到是隔2抽取,即對每個輸入樣本只有一個分支處于活躍狀態,那么還可以有更大程度的節省。這相當于把輸入序列分為兩個半采樣率序列,分別為奇次樣本和偶次樣本。然后將這些樣本應用到全通分支并加總。此外每個基本段內的延遲元可以在較低速率下運行 ,從而讓存儲需求減半。這個設計可以高效地實現流水線化并映射到一個DSPSlice,因為兩個分支的輸出濾波器可使用外部加法器進行累加。所以實現一個如圖4所示的五階隔2抽取IIR濾波器,只需要一個DSP48E1Slice。插值也存在類似的情況,由每個分支濾波器依次提供一個交織器的的樣本。另外,支持隔2插值也只需要一個DSPSlice。
A、B、C、D和P端口依據賽靈思7系列命名法[3]。您可以級聯DSPSlice來實現更高階的濾波器,而且由于采用雙分支結構,每個分支的流水線延遲相等。需要注意的是因為反饋路徑只能延遲2,需要使用三個內部寄存器的DSPSlice無法完全實現流水線化且。與在輸入端寄存相比,使用M寄存器可以在更高頻率下運行且功耗更小。當N=3或者更大的數時,既可以采用讓DSPSlice在最大頻率下運行的做法,也可以采用讓DSPSlice最大限度地實現流水線化的做法。后者可以通過讓濾波器在雙通道TDM模式下工作來實現,此時延遲元數量翻倍,A輸入反饋路徑使用Slice中的寄存器A1和A2,這樣C輸入之前的延遲就從3增加到5。
圖3:抽取(左圖)與插值(右圖)
圖4:隔2抽取,映射到賽靈思DSP48E1
量化和裕量
此類N帶結構已被命名為波數字濾波器(WDF),因為它們可以模擬經典模擬濾波器中的雙端無損梯形網絡。文獻中對此類含有橢圓響應的濾波器設計有全面的介紹。這種設計與用于模擬、數字域間轉換的雙線性變換相結合,為設計數字橢圓濾波器和巴特沃斯濾波器提供了有力的方法。使用梯形濾波器的另一個優勢在于此類結構沿襲了對系數量化低敏感度的特性。這意味著要在不含劣化等紋波特性的情況下實現能滿足100dB阻帶需求的濾波器,系數使用18位的字長度綽綽有余。對基本段[4]穩態增益特性的分析,發現增益最低的算術節點的最大增益為2.0,且發生在預加法器的輸出處。這對定點設計而言有著顯著的意義,因為它意味著我們只需要在預加法器輸出增加1位即可。在賽靈思DSP48E1Slice內的預加法器輸出沒有飽和邏輯存在,故將A和D的輸出限制為24位可以防止濾波器的運行發生數字溢出,以及更為重要的是,讓運行達到DSPSlice的最大內部精度。雖然穩態增益被限制在2.0,階梯響應下的瞬態會超過2.0,因此建議只使用23位,為安全運行留出裕量。對某些數據源,比如說24位音樂而言,您可利用預先知曉的信號特性,應用完全的動態范圍。
如果輸入數據不足24位,應在字中左對齊,因此會產生部分分數位。例如,對于16位輸入數據而言,理想的選擇是留出1位保護位、16位數據位和7位分數位。與浮點相比,一般只需要3到4位分數位就足以實現理想的精度。
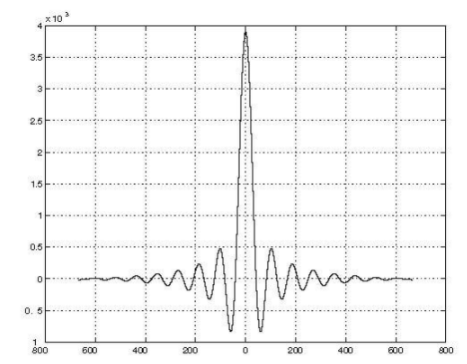
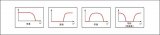
圖5:滿足相同阻帶(左圖)和通帶(右圖)規范的21階FIR濾波器和五階WDF
生成濾波器系數
R.A. Valenzuela和A.G. Constantinides[5]的專著中已充分介紹了采用雙分支結構實現為任何階數橢圓濾波器生成系數的方法。圖5所示的是一種標準化通帶為0.125的五階(兩個系數a0=0.1380,a1=0.5847)WDF濾波器,與使用帕克斯-麥克萊倫算法設計的22抽頭FIR濾波器相比,它能夠滿足相同的通帶紋波和阻帶衰減指標。結果表明濾波器階數通常下降到原來的1/4,且與FIR所用的11個乘法器相比(考慮對稱因素),WDF只需要兩個乘法器。
在半帶WDF中,阻帶和通帶紋波并非互不相干。不過通過合理設置阻帶衰減就能得到可忽略不計的通帶紋波。例如圖5中的濾波器的通帶紋波為10-6dB。FIR的優勢在于能夠單獨設定這兩個設計參數,這樣在給定階數的情況下,可以設定較高的通帶紋波來幫助滿足阻帶需求。
接下來我們來驗證一下如果不使用DSP48E1,而是通過高度量化系數在部分LE中實現濾波器情況會得到什么。回顧一下,由于WDF濾波器以模擬梯形濾波器原型為基礎,那么針對特定的通帶我們應該能夠找到低位密度的系數。比特 應盡量以標準分解方法寫入,從而最大程度地減少加法器的數量,如表1所示。
表1 - 三種樣本通帶的量化系數
雖然0.19通帶的五階濾波器的阻帶衰減已經不錯了,但是將兩個這樣的濾波器簡單級聯就可以得到阻帶為-78dB的10階濾波器。例如表1中的第一個抽取器可以用圖6中給出的少許幾行Verilog代碼來實現。
圖6:實現表1中第一個抽取濾波器的Verilog代碼
有效資源
我們已經展示了自然而然映射到插值和抽取中的IIR濾波器構建。該結構比IIR二階段甚至FIR都擁有更多有效資源。它能充分映射到DSP48E1Slice的預加法器/乘法器/后加法器中,且對于18位系數的定點量化效應十分穩健,從而給出可控制的100dB阻帶。一些無乘法器五階設計可允許用于特定通帶寬,可將其映射到一些邏輯寄存器和加法器中以降低DSP資源占用。
參考文獻:
1. 賽靈思白皮書WP330,《賽靈思FPGA中的無限脈沖響應濾波器結構》,2009年8月;
2. 作者:P.P. Vaidyanathan,《多速率系統和濾波器組》,Prentice-Hall出版社,紐約州Englewood Cliffs,1993年;
3. 《賽靈思7系列DSP48E1 Slice用戶指南》,1.5版本,2013年4月3日;
4. 作者:Artur Krukowski,Richard Morling,Izzet Kale,《多相位N路徑IIR結構量化效應》,IEEE儀器測量匯刊,第51卷第6號,2002年12月;
5. 作者:R.A. Valenzuela和A.G. Constantinides,《高效率插值抽取數字信號處理方案》,電子電路和系統,IEEE會議記錄第G部分第130卷第6號,1983年。
 電子發燒友App
電子發燒友App

































評論