在本文中,我們將討論如何在系統(tǒng)仿真中對(duì)ADC進(jìn)行建模的另一種方法,這次是使用有效位數(shù),并通過(guò)在理想量化器輸入中引入5階多項(xiàng)式來(lái)調(diào)整ADC。 到目前為止,在本系列中,我們已經(jīng)討論了各種優(yōu)點(diǎn) 在系統(tǒng)仿真
2023-05-03 15:34:00 1055
1055 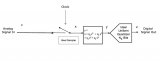
([0 0.515 0pi/20]);L5=Link([pi00pi/20]);L6=Link([0 0.08000]);[q ,qd, qdd]=jtraj(q1,q2,50); %五次多項(xiàng)式軌跡,得到關(guān)節(jié)角度,角速度,角加速度,50為采樣點(diǎn)個(gè)數(shù)T=robot.fkine(q);%末端執(zhí)行器位姿`
2019-03-13 10:09:51
最近在學(xué)習(xí)CRC校驗(yàn),根據(jù)生成多項(xiàng)式,通過(guò)編碼代碼實(shí)現(xiàn)CRC校驗(yàn),就是不知道怎么實(shí)現(xiàn),求實(shí)現(xiàn)CRC校驗(yàn)的原理過(guò)程?
2015-01-05 16:17:27
最近在嘗試CRC校驗(yàn),根據(jù)生成多項(xiàng)式,通過(guò)編碼代碼實(shí)現(xiàn)CRC校驗(yàn),就是不知道怎么實(shí)現(xiàn),求實(shí)現(xiàn)CRC校驗(yàn)的原理過(guò)程,希望大神幫忙指點(diǎn)一下,不勝感激,或者有學(xué)習(xí)這方面知識(shí)的和我一起探討一下也好啊!
2014-12-03 14:55:37
;
根據(jù)本原多項(xiàng)式,確定C0至Cn的取值,在圖4找到對(duì)應(yīng)的所有反饋支路;
根據(jù)反饋支路寫出針對(duì)最高位的反饋表達(dá)式。
例如,在構(gòu)建一個(gè)級(jí)數(shù)n=8的m序列時(shí):
m序列的Verilog實(shí)現(xiàn)
源代碼:
仿真結(jié)果
2023-11-06 17:03:26
CPLD 是可以等價(jià)于 GAL 的陣列,編程的數(shù)學(xué)模型是基于多項(xiàng)式的乘用與門電路實(shí)現(xiàn),而多項(xiàng)式的加用或門電路實(shí)現(xiàn)。那么我們 FPGA 的編程機(jī)理是什么呢?它為什么能夠實(shí)現(xiàn)我們?nèi)我獾暮瘮?shù)表達(dá)式呢?我們
2021-07-30 06:39:06
多項(xiàng)式回歸示例(sklearn實(shí)現(xiàn))
2019-05-20 06:42:09
多項(xiàng)式線性擬合
2013-04-18 10:54:53
本文采用FPGA 和MicroBlaze 進(jìn)行嵌入式系統(tǒng)設(shè)計(jì),文中在分析了FFT算法后,描述了運(yùn)算的蝶形單元,地址生成單元及FFT的實(shí)現(xiàn)過(guò)程。從實(shí)際設(shè)計(jì)出發(fā),完成了基于FPGA的單精度浮點(diǎn)運(yùn)算
2021-02-22 07:36:49
自動(dòng)白平衡的FPGA實(shí)現(xiàn)采用FPGA對(duì)自動(dòng)白平衡進(jìn)行運(yùn)算有什么優(yōu)點(diǎn)?
2021-04-13 06:20:46
CAN 節(jié)點(diǎn)中設(shè)有錯(cuò)誤檢測(cè)、標(biāo)定和自檢等措施。檢測(cè)錯(cuò)誤包括多種方式,其中最常用、最有效的一種是 CRC 校驗(yàn)。CRC 序列由循環(huán)冗余校驗(yàn)碼求得的幀檢查序組成。為實(shí)現(xiàn) CRC 計(jì)算,被除的多項(xiàng)式系數(shù)由
2018-12-24 10:28:14
本帖最后由 dianzi_fans 于 2011-12-3 12:03 編輯
原理1.通信雙方約定同一個(gè)生成多項(xiàng)式 例如16位的CRC碼得生成多項(xiàng)式G(X)=X16+X15+X2+1即
2011-12-02 23:47:05
Labview-多項(xiàng)式標(biāo)定算法
2015-08-19 12:23:39
MATLAB多項(xiàng)式函數(shù)命令Roots 求多項(xiàng)式根 Poly 構(gòu)造具有指定根的多項(xiàng)式 Polyvalm 帶矩陣變量的多項(xiàng)式計(jì)算 Residue 部分分式展開(kāi)(留數(shù)計(jì)算) Polyfit 數(shù)據(jù)的多項(xiàng)式擬合 Polyder 微分多項(xiàng)式 Conv 多項(xiàng)式乘法 Deconv 多項(xiàng)式除法
2009-09-22 16:01:12
運(yùn)算在MATLAB中分別是通過(guò)conv()和deconv()來(lái)實(shí)現(xiàn),同時(shí)卷積和反卷積也是使用這兩個(gè)函數(shù)。格式如下w=conv(u,v)[q,r]=deconv(v,u) r為余子式5、多項(xiàng)式的微分
2014-07-21 10:48:26
分享一個(gè):Matlab多項(xiàng)式運(yùn)算功能的程序代碼Matlab的符號(hào)運(yùn)算功能強(qiáng)大,看了些資料,都比較啰嗦,然后再次總結(jié)為一個(gè)m文件測(cè)試大部分符號(hào)運(yùn)算功能%% 符號(hào)變量與符號(hào)表
2011-10-02 13:42:45
m 序列的 matlab 仿真實(shí)現(xiàn) 用 matlab 編程求本原多項(xiàng)式 本仿真中采用四級(jí)移位寄存器, 產(chǎn)生周期為 15 的 m 序列。 對(duì)應(yīng) n=4 的 m 序列的本原多項(xiàng)式求解程序如下: n
2019-06-20 04:20:27
本文以戰(zhàn)術(shù)軍用通信系統(tǒng)的首選碼RS(31,15)碼為例,對(duì)生成多項(xiàng)式進(jìn)行了優(yōu)化,并采用查表法的原理極大地提高了編碼器運(yùn)算數(shù)據(jù)的能力,縮短了運(yùn)算周期,最終利用VHDL語(yǔ)言編譯,在FPGA中實(shí)現(xiàn),得到了正確的RS編譯碼。
2021-05-06 09:27:33
原子哥,在你的SPI實(shí)驗(yàn)(庫(kù)函數(shù)版本)中有這樣的一句話: SPI_InitStructure.SPI_CRCPolynomial = 7; //CRC值計(jì)算的多項(xiàng)式不知道設(shè)置它是做什么用的????????????
2020-04-09 04:35:13
采用的是grilling的三門限準(zhǔn)則',端點(diǎn)效應(yīng)抑制采用的是經(jīng)典的鏡像延拓法。我剛文獻(xiàn)中有極值延拓法、多項(xiàng)式擬合延拓法等很多改進(jìn)方法,他們是怎么在matlab上實(shí)現(xiàn)?我學(xué)習(xí)matlab時(shí)間不長(zhǎng),真心不知道如何下手?希望做過(guò)這方面的前輩指教!萬(wàn)分感激!
2016-07-26 11:47:43
2.2 3.3 4.4 5.5 6.6 7.7 8.8],Z=[1 2 3 4 5 6 7 8 9],Z=f(x,y)。怎么利用labview編寫實(shí)現(xiàn)二元多項(xiàng)式擬合?求出各個(gè)參數(shù)。labview中的多項(xiàng)式擬合,只能做一元的,不知道怎么做?或者是應(yīng)該怎么把二元的轉(zhuǎn)成一元的來(lái)做呢?
2013-11-27 14:10:40
來(lái)說(shuō),二者將產(chǎn)生不同的結(jié)果。多項(xiàng)式的表示方法和運(yùn)算p(x)=x^3-3x-5 可以表示為p=[1 0 –3 5],求x=5時(shí)的值用plotval(p,5)也可以求向量:a=[3 4 5],plotval(p
2012-02-08 15:23:17
多項(xiàng)式(只能被1和自身整除,類似于質(zhì)數(shù))時(shí)才能產(chǎn)生M序列。這里給出2階到10階的本原多項(xiàng)式1.4 FPGA實(shí)現(xiàn) 我們以7階、8階本原多項(xiàng)式為例設(shè)計(jì)兩個(gè)M序列發(fā)生器 1.4.17階架構(gòu)設(shè)計(jì)注:+ 代表異
2020-04-15 13:55:22
一種新的記憶多項(xiàng)式預(yù)失真器摘要:提出了一種新的記憶多項(xiàng)式預(yù)失真器,對(duì)寬帶功率放大器進(jìn)行線性化.該方法主要利用非均勻時(shí)延來(lái)設(shè)計(jì)預(yù)失真器.軟件仿真結(jié)果表明:當(dāng)輸入為寬帶信號(hào)時(shí),與傳統(tǒng)的無(wú)記憶預(yù)失真技術(shù)
2009-08-08 09:52:45
處理系統(tǒng)中最重要的部件之一。FPGA是當(dāng)前數(shù)字電路研究開(kāi)發(fā)的一種重要實(shí)現(xiàn)形式,它與全定制ASIC電路相比,具有開(kāi)發(fā)周期短、成本低等優(yōu)點(diǎn)。但多數(shù)FPGA不支持浮點(diǎn)運(yùn)算,這使FPGA在數(shù)值計(jì)算、數(shù)據(jù)分析和信號(hào)
2019-07-05 06:21:42
的分母為系統(tǒng)的特征多項(xiàng)式;極點(diǎn):特征多項(xiàng)式等于0組成特征方程的根;階數(shù):特征多項(xiàng)式的最高階數(shù)n;根軌跡增益:;拉普拉斯變換:可采用傳遞函數(shù)代替常系數(shù)微分方程來(lái)描述系統(tǒng)的特性。這就為采用直觀和簡(jiǎn)便的圖解方法來(lái)確定控制系統(tǒng)的整個(gè)特性、分析控制系統(tǒng)的運(yùn)動(dòng)過(guò)程,以及提供控制系統(tǒng)調(diào)整的可能性。
2019-05-21 08:43:40
在引用一個(gè)公式節(jié)點(diǎn)計(jì)算多項(xiàng)式的值,出現(xiàn)定義錯(cuò)誤,不知道出現(xiàn)了什么問(wèn)題,沒(méi)有輸入的中間變量y我應(yīng)該是要自己定義的吧
2018-09-23 22:27:57
MATLAB求多項(xiàng)式的系數(shù):單變量:syms x yf1=x^4+2*x+1;f2=y^6+5*y^3+3;f3=x^5+2*x^3*y^4+x*y^2+4;c = sym2poly(f1)c
2011-10-02 13:41:08
橢圓曲線加密是一種目前已知的所有公鑰密碼體制中能夠提供最高比特強(qiáng)度的一種公鑰體制。在FPGA實(shí)現(xiàn)橢圓曲線加密系統(tǒng)時(shí),基于GF(2)的多項(xiàng)式有限域中的乘法、求逆運(yùn)算是其中的兩大難點(diǎn)。
2019-10-10 07:36:43
你好,我正在用不同的方法用 04C11DB7 多項(xiàng)式計(jì)算 CRC32:通過(guò) python binascii.crc32(...),以及在 STM32G483 上使用 ST 嵌入式模塊.在諸如
2022-12-27 08:10:38
`m序列的本原多項(xiàng)式f(x)=1+x^2+x^3+x^4+x^8。題目要求見(jiàn)圖:`
2013-09-07 15:18:41
見(jiàn)的單比特線性函數(shù):對(duì)寄存器的某些位進(jìn)行異或操作后作為輸入,再對(duì)寄存器中的各比特進(jìn)行整體移位。線性反饋移位寄存器通常由動(dòng)態(tài)或靜態(tài)主從型觸發(fā)器構(gòu)成。反饋回路由異或門構(gòu)成。其特性通常由一個(gè)特征多項(xiàng)式表征
2023-04-21 19:42:13
)=x6+x5+x4+x3+x3+x3+x2+x1+x0得到結(jié)果后,合并同類項(xiàng)時(shí)采用模2運(yùn)算。也就是說(shuō)乘除法采用正常的多項(xiàng)式乘除法,而加減法都采用模2運(yùn)算。所謂模2運(yùn)算就是結(jié)果除以2后取余數(shù)。比如3 mod 2 = 1。因此,上面最終得到的多項(xiàng)式為
2016-06-19 16:44:39
本帖最后由 一只耳朵怪 于 2018-5-21 11:23 編輯
想用labview進(jìn)行如圖所示的公式計(jì)算,我找到了多項(xiàng)式插件,但是沒(méi)研究明白怎么實(shí)現(xiàn)上面是常數(shù)下面是多項(xiàng)式這種形式的多項(xiàng)式的運(yùn)算,不知道能否請(qǐng)各位大佬指點(diǎn)一二,最好能給出相應(yīng)的程序,圖中除了x之外都是變量。
2018-05-21 11:03:27
時(shí),CRC為 11001011.在網(wǎng)上下載的CRC計(jì)算器按照芯片手冊(cè)上的多項(xiàng)式算出來(lái)的也不一樣,誰(shuí)能幫我看一下是怎么計(jì)算的,謝謝!!
2016-06-13 08:50:39
求這個(gè)不定積分的近似表達(dá)式,matlab符號(hào)運(yùn)算可以求嗎?大家一起來(lái)想想辦法,無(wú)論什么辦法,只要能得到最終簡(jiǎn)潔的近似表達(dá)式即可,比如多項(xiàng)式。。
2016-04-07 23:15:43
我想實(shí)現(xiàn)的是將大量數(shù)據(jù)樣本點(diǎn)通過(guò)最小二乘法進(jìn)行曲面擬合,最小二乘法和插值法不同的是,擬合無(wú)需過(guò)每一個(gè)點(diǎn)。保證R值最好就可以了但是滿足最小二乘法的多項(xiàng)式形式有很多,按照不同的數(shù)據(jù),可以采用多種
2017-07-03 21:51:18
FPGA如何實(shí)現(xiàn)32位減法運(yùn)算
2019-02-28 04:59:09
最近在學(xué)習(xí)CRC校驗(yàn),根據(jù)生成多項(xiàng)式,通過(guò)編碼代碼實(shí)現(xiàn)CRC校驗(yàn),就是不知道怎么實(shí)現(xiàn),求實(shí)現(xiàn)CRC校驗(yàn)的原理過(guò)程。
2019-05-21 02:21:36
XCOM串口助手的CRC16用的多項(xiàng)式是哪個(gè)?XCOM能否加個(gè)計(jì)算CRC16的功能?謝。
2019-09-02 22:29:58
嗨,我正在開(kāi)展一個(gè)需要表征SOLT校準(zhǔn)套件的項(xiàng)目。該套件代表從3.5mm SMA連接器到長(zhǎng)度為20mm的微帶線的過(guò)渡。對(duì)3GHz以上頻率的測(cè)量需要將開(kāi)放邊緣電容模型化為3階多項(xiàng)式。我執(zhí)行以下步驟:在
2019-05-08 07:44:04
的擾碼數(shù)值,是由當(dāng)前狀態(tài)和之前發(fā)送狀態(tài)數(shù)值進(jìn)行模二加法運(yùn)算(異或)將結(jié)果輸出。而具體是之前的那個(gè)狀態(tài)呢?就是本院多項(xiàng)式中系數(shù)為一的項(xiàng),如我們上面的例子中系數(shù)為1的項(xiàng)指數(shù)為39和58,那么我們就要將當(dāng)前
2019-07-31 16:30:47
介紹有限域Chebyshev多項(xiàng)式的定義和性質(zhì)。針對(duì)基于有限域Chebyshev多項(xiàng)式的類ElGamal公鑰密碼系統(tǒng)存在的弱點(diǎn),提出一個(gè)新的公鑰密碼算法。該算法的公開(kāi)密鑰隱藏了求秘密密鑰的信息
2009-04-08 08:36:04 13
13 該文針對(duì)由記憶多項(xiàng)式設(shè)計(jì)的功率放大器預(yù)失真系統(tǒng),提出了一種新的分?jǐn)?shù)階記憶多項(xiàng)式預(yù)失真器。提出預(yù)失真多項(xiàng)式是在常用記憶多項(xiàng)式基礎(chǔ)上,通過(guò)去掉偶數(shù)階項(xiàng)增加分?jǐn)?shù)階項(xiàng)
2009-11-10 15:50:59 10
10 3.1 多項(xiàng)式一、多項(xiàng)式的建立 1、多項(xiàng)式的表示(1)一般都是按未知量的降冪排列各項(xiàng)之和(2)在MATLAB中,用它的系數(shù)矢量來(lái)表示多項(xiàng)式:2、創(chuàng)建多項(xiàng)式的方法
2009-11-24 09:20:40 0
0 一種新的記憶多項(xiàng)式預(yù)失真器
提出了一種新的記憶多項(xiàng)式預(yù)失真器,對(duì)寬帶功率放大器進(jìn)行線性化.該方法主要利用非均勻時(shí)延來(lái)設(shè)計(jì)預(yù)失真器.軟件仿真結(jié)果表
2010-02-23 10:08:49 9
9 多項(xiàng)式方程求根的魔術(shù)植物栽培算法1974年6月, 第一次不動(dòng)點(diǎn)(fixed points) 算法及應(yīng)用國(guó)際會(huì)議在美國(guó)召開(kāi)。歐洲、日本和美國(guó)的幾十位數(shù)學(xué)家參加了這次會(huì)議。美國(guó)
2010-02-25 13:58:25 13
13 線性反饋移位寄存器( σ -LFSR)是基于字設(shè)計(jì)的,在安全性和效率上達(dá)到較好折衷的一種反饋移位寄存器。σ -LFSR 輸出序列的特征多項(xiàng)式為有限域上的矩陣多項(xiàng)式。該文利用有限域上矩
2010-03-06 11:36:34 14
14 摘 要: 橢圓曲線加密是一種目前已知的所有公鑰密碼體制中能夠提供最高比特強(qiáng)度的一種公鑰體制。在FPGA實(shí)現(xiàn)橢圓曲線加密系統(tǒng)時(shí),基于GF(2)的多項(xiàng)式有限域中的乘法、求逆運(yùn)算是其中的兩大難點(diǎn)。
2006-03-11 13:17:30 1272
1272 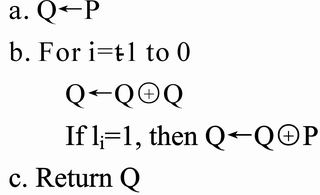
二次多項(xiàng)式發(fā)生器
2009-09-22 17:53:03 618
618 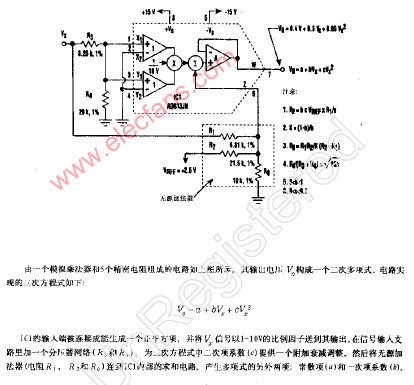
采用雙運(yùn)算核在FPGA硬件平臺(tái)上實(shí)現(xiàn)小波變換模塊。采用單一時(shí)鐘,在不增加系統(tǒng)設(shè)計(jì)復(fù)雜性和功耗的情況下,使得系統(tǒng)達(dá)到實(shí)時(shí)處理的要求。系統(tǒng)通過(guò)仿真驗(yàn)證,工作穩(wěn)定可靠。
2011-12-07 13:59:56 22
22 基于FPGA的開(kāi)方運(yùn)算實(shí)現(xiàn) ,的技術(shù)論文
2015-10-30 10:59:01 5
5 本文提出了一種基于拉格朗日插值多項(xiàng)式的光伏電池I-V特性的新的建模方法。該方法利用桑迪亞(Sandia)國(guó)家重點(diǎn)實(shí)驗(yàn)室I-V特性曲線上的五個(gè)點(diǎn)的值作為節(jié)點(diǎn)進(jìn)行拉格朗日插值,最終得到 特性顯式表達(dá)
2016-01-04 17:13:49 22
22 三次多項(xiàng)式型段內(nèi)加減速控制新方法,下來(lái)看看
2016-05-03 09:38:54 16
16 多項(xiàng)式擬合柔性加減速算法的研究,下來(lái)看看。
2016-05-03 14:23:26 7
7 多項(xiàng)式加減速控制方法研究,有需要的下來(lái)看看
2016-05-03 14:23:26 7
7 基于多項(xiàng)式插值函數(shù)的翼型參數(shù)化設(shè)計(jì)方法_張明輝
2016-12-29 14:40:19 2
2 一種基于多項(xiàng)式調(diào)和表示的拉普拉斯濾波核_杜振龍
2017-01-07 20:32:20 0
0 多項(xiàng)式直接擬合在鉑電阻高精度測(cè)溫中的研究_吳志祥
2017-01-12 22:28:02 1
1 自適應(yīng)細(xì)分二次多項(xiàng)式響應(yīng)面算法_羅小玲
2017-03-19 11:41:51 0
0 基于Laguerre多項(xiàng)式的LVDT位移傳感器非線性校正_譚永宏
2017-03-19 19:08:35 2
2 P、,和P、D對(duì)系統(tǒng)的穩(wěn)定誤差進(jìn)行數(shù)據(jù)采樣;其次,應(yīng)用三階多項(xiàng)式響應(yīng)面法對(duì)數(shù)據(jù)進(jìn)行建模,建立多項(xiàng)式響應(yīng)面模型解析式,并用Mat-lah軟件對(duì)模型進(jìn)行可視化。最后的計(jì)算結(jié)果表明,所建模型精度較高,為整定優(yōu)化控制參數(shù)奠定了建模基礎(chǔ)。
2017-11-13 10:48:07 9
9 正交多項(xiàng)式擬合:給定函數(shù)f(x)在m個(gè)采樣點(diǎn)處的值f(xi)以及每個(gè)點(diǎn)的權(quán)重wi,求曲線擬合的正交多項(xiàng)式Pn(x)滿足最小二乘誤差||err||2=∑mi=1wi[f(xi)?Pn(xi)]2《TOL。
2017-11-27 15:29:01 7684
7684 彈道修正彈內(nèi)的彈載計(jì)算機(jī)必須實(shí)時(shí)對(duì)衛(wèi)星定位接收機(jī)獲取的彈丸狀態(tài)數(shù)據(jù)進(jìn)行濾波降噪,用于預(yù)測(cè)彈丸落點(diǎn),傳統(tǒng)濾波方法濾波時(shí)間長(zhǎng),濾波實(shí)時(shí)性差,提出一種基于多項(xiàng)式擬合的方法。通過(guò)適當(dāng)降低衛(wèi)星定位接收機(jī)數(shù)據(jù)
2017-12-19 15:54:01 0
0 本文運(yùn)用局部多項(xiàng)式的方法對(duì)圖像進(jìn)行插值。文中我們從一幅高分辨率圖像通過(guò)下采樣得到一張低分辨率圖像,然后對(duì)其進(jìn)行插值并求出插值圖像的峰值信噪比(PSNR)。為說(shuō)明本文方法的可行性,我們把本文的方法
2017-12-20 10:02:23 1
1 多項(xiàng)式插值技術(shù)是近似理論中一種常見(jiàn)的近似方法,被廣泛用于數(shù)值分析、信號(hào)處理等領(lǐng)域。但傳統(tǒng)的多項(xiàng)式插值技術(shù)大多是基于數(shù)值分析與實(shí)驗(yàn)結(jié)果相結(jié)合得到的,沒(méi)有統(tǒng)一的理論描述和規(guī)律性的解決方案。為此,根據(jù)密切
2018-01-05 13:55:39 0
0 針對(duì)傳統(tǒng)基于插值多項(xiàng)式的秘密分享方案,需要復(fù)雜的多項(xiàng)式運(yùn)算,當(dāng)涉及的數(shù)據(jù)比較大時(shí),運(yùn)算效率特別低的問(wèn)題,提出一種結(jié)合數(shù)據(jù)分塊方法以及僅需要在GF(2)上的異或運(yùn)算的秘密分享方案,并應(yīng)用于大規(guī)模
2018-01-07 12:05:05 0
0 針對(duì)傳統(tǒng)常模算法收斂速度慢、均方誤差大以及傳統(tǒng)神經(jīng)網(wǎng)絡(luò)參數(shù)多、復(fù)雜度高的問(wèn)題,提出了基于非線性Volterra信道的復(fù)數(shù)神經(jīng)多項(xiàng)式盲均衡算法(Fuzzy neural networkcomplex
2018-02-26 15:00:43 0
0 結(jié)構(gòu)復(fù)雜,采用DSP實(shí)現(xiàn)會(huì)增加系統(tǒng)負(fù)擔(dān),降低系統(tǒng)速度。在某些對(duì)速度要求較高的情況,必須采用專門的浮點(diǎn)運(yùn)算處理器。 EDA/FPGA技術(shù)不斷發(fā)展,其高速、應(yīng)用靈活、低成本的優(yōu)點(diǎn)使其廣泛應(yīng)用數(shù)字信號(hào)處理領(lǐng)域。在FPCA技術(shù)應(yīng)用的初期,
2018-04-10 14:25:53 17
17 開(kāi)方運(yùn)算作為數(shù)字信號(hào)處理(DSP)領(lǐng)域內(nèi)的一種基本運(yùn)算,其基于現(xiàn)場(chǎng)可編程門列(FPGA)的工程實(shí)現(xiàn)具有較高的難度。本文分析比較了實(shí)現(xiàn)開(kāi)方運(yùn)算的牛頓-萊福森算法,逐次逼近算法,非冗余開(kāi)方算法3種算法
2020-08-06 17:58:15 6
6 該CRC-8的生成多項(xiàng)式為G(D)=D8+D2+D+1,對(duì)CRC進(jìn)行簡(jiǎn)化表示時(shí)可以忽略最高位的D8,結(jié)合圖示中三個(gè)異或運(yùn)算的位置更容易理解生成多項(xiàng)式,8位CRC有8個(gè)寄存器C0~C7,根據(jù)多項(xiàng)式,C0、C1和C2的輸入是由異或運(yùn)算而來(lái);
2021-03-12 17:47:57 6194
6194 針對(duì)傳統(tǒng)基于多項(xiàng)式分布的主題模型不能較好地刻畫文檔中詞匯突發(fā)的現(xiàn)象,綜合考慮文本集固有的時(shí)間信息,提出一種面向詞匯突發(fā)的 Dirichlet組合多項(xiàng)式(DCM)連續(xù)時(shí)間主題模型。采用 DCM 分布
2021-03-16 11:36:10 35
35 一個(gè)基于RLWE難題的多項(xiàng)式環(huán)上的同態(tài)承諾方案,然后基于承諾方案設(shè)計(jì)一個(gè)∑協(xié)議,并利用Fiat- Shamir轉(zhuǎn)化方法將該∑協(xié)議轉(zhuǎn)化為可鏈接環(huán)簽名方案,最后基于該可鏈接環(huán)簽名方案提岀一個(gè)簡(jiǎn)易的數(shù)字貨幣模型。安全分析表明,由于所提方案基于RLWE困難問(wèn)題構(gòu)
2021-04-12 11:33:09 5
5 真實(shí)時(shí)間以太網(wǎng)多項(xiàng)式(REM)交換機(jī)
2021-05-24 18:56:08 2
2 AGW準(zhǔn)則和分段方法是構(gòu)造有限域上置換多項(xiàng)式的兩種主要方法。介紹有限域上置換多項(xiàng)式在密碼學(xué)和編碼理論中的應(yīng)用,總結(jié)利用AGW準(zhǔn)則和分段方法構(gòu)造有限域上置換多項(xiàng)式和逆置換的研究進(jìn)展,闡述置換多項(xiàng)式存在的問(wèn)題,并對(duì)下一步研究工作進(jìn)行展望。
2021-06-08 14:36:46 7
7 有些FPGA中是不能直接對(duì)浮點(diǎn)數(shù)進(jìn)行操作的,只能采用定點(diǎn)數(shù)進(jìn)行數(shù)值運(yùn)算。對(duì)于FPGA而言,參與數(shù)學(xué)運(yùn)算的書就是16位的整型數(shù),但如果數(shù)學(xué)運(yùn)算中出現(xiàn)小數(shù)怎么辦呢?要知道,FPGA對(duì)小數(shù)是無(wú)能為力
2021-08-12 09:53:39 4504
4504 FPGA中的硬件邏輯與軟件程序的區(qū)別,相信大家在做除法運(yùn)算時(shí)會(huì)有深入體會(huì)。若其中一個(gè)操作數(shù)為常數(shù),可通過(guò)簡(jiǎn)單的移位與求和操作代替,但用硬件邏輯完成兩變量間除法運(yùn)算會(huì)占用較多的資源,電路結(jié)構(gòu)復(fù)雜,且通常無(wú)法在一個(gè)時(shí)鐘周期內(nèi)完成。因此FPGA實(shí)現(xiàn)除法運(yùn)算并不是一個(gè)“/”號(hào)可以解決的。
2022-04-27 09:16:03 6099
6099 FPGA實(shí)現(xiàn)加法和減法運(yùn)算非常簡(jiǎn)單,實(shí)現(xiàn)乘法和除法可以用IP,那實(shí)現(xiàn)對(duì)數(shù)和指數(shù)運(yùn)算該用什么呢?
2023-08-05 09:37:05 810
810 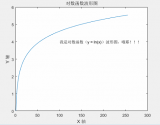
該CRC-8的生成多項(xiàng)式為G(D)=D8+D2+D+1,對(duì)CRC進(jìn)行簡(jiǎn)化表示時(shí)可以忽略最高位的D8,結(jié)合圖示中三個(gè)異或運(yùn)算的位置更容易理解生成多項(xiàng)式,8位CRC有8個(gè)寄存器C0~C7,根據(jù)多項(xiàng)式,C0、C1和C2的輸入是由異或運(yùn)算而來(lái);
2023-11-12 09:53:17 1173
1173 
五次多項(xiàng)式插值法 五次多項(xiàng)式有6個(gè)待定系數(shù),可同時(shí)對(duì)起始點(diǎn)和目標(biāo)點(diǎn)的角度、角速度和角加速度給出約束條件。 數(shù)學(xué)推導(dǎo) MATLAB代碼 %五次多項(xiàng)式插值法 clear;clc;q_array
2023-11-17 15:57:42 548
548 
 電子發(fā)燒友App
電子發(fā)燒友App

























評(píng)論