電子可重構，或者說電調微波濾波器由于其在改善現在及未來微波系統容量中不斷提高的重要性而正吸引著人們越來越多的關注來對其進行研究和開發。例如，嶄露頭腳的超寬帶（UWB）技術要求使用很寬的無線電頻譜。然而，作為資源的頻譜是寶貴而有限的，因此，頻譜總是被用于多種用途，這意味著當諸如UWB 無線系統這種操作受到關注時，頻譜上充滿著不期望的信號。在這種情況下，現存的時時處處都在發生變化的不期望的窄帶無線電信號有可能會干擾UWB 系統的波段。這種問題的解決方案是在UWB 帶通濾波器的通帶上引入了一個可進行電切換或電調諧的狹窄的抑制帶（陷波）。這種電子可重構濾波器也是寬帶雷達或電子軍用系統所渴望得到的。我們可以來未雨綢繆地考慮未來的認知無線電和雷達應用，可以肯定的是，可進行電子重構的微波濾波器將會在無線系統中起到一個更重要的作用。

一般來說，為了開發電子可重構濾波器，有源切換元件或調諧元件，如半導體p-i-n 和變容器二極管，射頻（RF）微機電系統（MEMS）或其它基于功能性材料的元件，包括鐵電體變容器，需要被集成進入無源濾波器結構中。由于微帶線濾波器[1]能夠便于以很小的尺寸來完成這類集成，因此，人們對于在微帶線的基礎上開發可調諧或可重構濾波器的興趣日益增加[2]-[36]。這些濾波器可以分類為可調諧梳狀帶通濾波器[2]-[9]，射頻微機電系統可調諧濾波器[10]-[15]，壓電傳感器（PET）可調諧濾波器[17]-[19]，可調諧高溫超導（HTS）濾波器[21]-[23]，可重構UWB 濾波器[24]-25]，可調諧雙頻段濾波器[26]，可調諧帶阻濾波器[27]-[31]，可重構/可調諧雙模濾波器[32]-[36]，以及基于可切換延遲線的可重構帶通濾波器。下面，我們將要介紹若干新近開發出來的典型的電子可重構微帶線濾波器。

可調諧梳狀濾波器

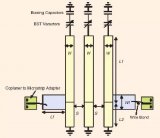
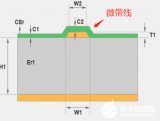
微帶線梳狀濾波器是開發可調諧或者說可重構帶通濾波器頗受歡迎的結構[2]-[9]。圖1 是一個3-極點可調諧梳狀濾波器的示意圖，其中每一個長度小于工作頻率的四分之一波長的微帶線諧振器的一端是短路相接的，另一端則加載一只變容器。在這個例子中，變容器是基于鐵電體鈦酸鍶鋇（BST）薄膜的。每一個BST 變容器的偏置網絡包含有一個與變容器相串聯的隔直電容器。帶通濾波器的中心頻率可以通過改變施加到變容器的直流偏置來進行電子調諧。

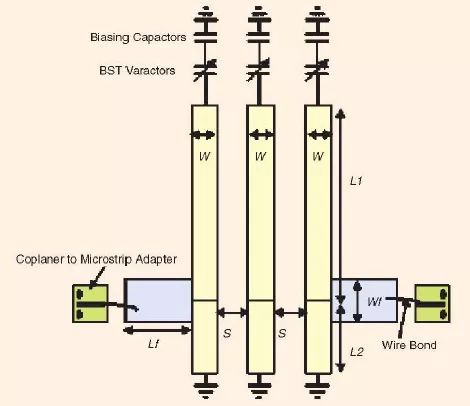
圖1、一個可調諧梳狀帶通濾波器的示意圖[2]。

圖2 舉例說明了與BST 薄膜進行單片集成的可調諧梳狀濾波器的制作和其測量性能。正如在文獻[3]中所報道的，對于直流偏置，在BST 薄膜之上，又沉積了一層阻性氮化鉭（TaN）薄膜并制作相應的圖案。TaN 薄膜的表面電阻率大約是1-10KΩ/每單位面積(Square)，被用來將直流偏置信號導引到電路上，而同時將對電路射頻性能的影響減到最小。將BST 薄膜電容器與鋁土基片，銅電極，和過孔相集成，從若干個方面推進了可調諧介電技術，這種調諧技術可以開發更復雜的射頻和微波電路。

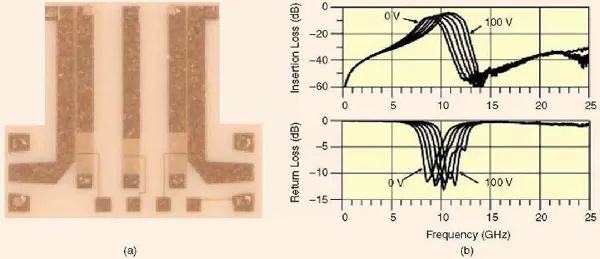
圖2、(a)一個采用了鈦酸鍶鋇薄膜的X-波段（8-12GHz）梳狀可調諧濾波器和(b)其測試性能[3]。

在進行中心頻率調諧時所出現的帶寬波動是一個眾所周知的問題。一般來說，為了保持一個與調諧頻率無關的絕對的通帶帶寬，耦合系數必須與調諧頻率成反比。已經存在一些解決這個問題的技術，例如文獻[4]和[8]。在文獻[8]中，人們研究了采用階梯阻抗微帶線諧振器的變容器調諧梳狀帶通濾波器，這樣可以更好地控制諧振器之間的耦合，從而可以通過使用較短電長度的線段元件來滿足恒定帶寬的要求。同時，人們采用了集總式電感器來作為輸入和輸出耦合網絡，從而使得外部品質因數（Q）直接隨著調諧頻率而變化。人們已經演示了這種類型的一個四極點濾波器，在2GHz下250MHz 的調諧范圍內，3-dB 通帶帶寬的變化小于3.2%。

在文獻[4]中，理論分析表明，對于一個可調諧N-極點濾波器，N 是諧振器的數量，其品質因數（figure of merit） 定義為通帶中心頻率的偏移與平均通帶的比值，它取決于損耗或調諧變容器的Q 值及濾波器的階數。由于Q 是與功率損耗成反比的，損耗越大，Q 值就越小。一般來說，品質因數（或調諧范圍）在小Q 值及大N 值的條件下會有所降低。

人們可以通過實施源/負載多諧振器耦合來設計具有多個傳輸零點以改善上阻帶性能的可調諧平面梳狀濾波器。正如在文獻[9]中所演示的，這可以通過在經典梳狀構造中增加兩個新的耦合線而得以實現，如圖3（a）所示，其中我們可以看見兩條薄的線從源/負載端伸向內部諧振器。圖3（b）繪制了所測得的具有分布在上阻帶的五個傳輸零點的濾波器的性能。濾波器的中心頻率可以在750MHz 到900MHz 之間進行調諧，濾波器使用的是Philips 公司的BB149 變容二極管，在0V 到20V 的偏置電壓下，這個二極管電容值的變化范圍是2 到20pF。變容器的偏置元件是6.8pF 和22nH。

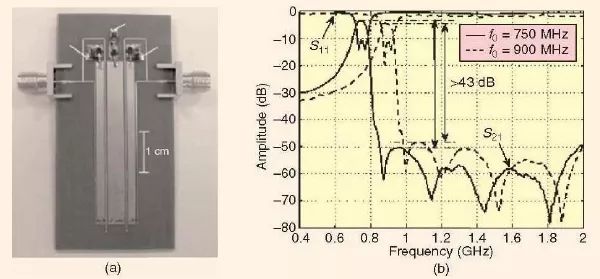
圖3、(a) 所制作的采用源/負載多諧振器耦合的3-極點電調梳狀濾波器和(b)它的測量響應[9]。

射頻微機電系統可重構濾波器

采用射頻微機電系統可重構濾波器而不是變容器來改變諧振器濾波器中諧振器的長度或其電路參數則形成了第二類可重構濾波器[10]-[15]。在這種情況下，電子調諧通常是采用數字方法來實現的，這種方法可以實現具有良好性能的大的調諧范圍，這包含了低損耗和高線性度。圖4 展示了一個這種類型的濾波器的例子。在這種情況下，正如文獻[11]中所報道的，這種拓撲結構是基于分布式半波長微帶線諧振器上的，而這種諧振器則是在高阻性硅基片上制作的。這是一個具有兩個諧振器的帶通濾波器，在每一個諧振器的末端添加一個容性貼片，這便允許低損耗地實現一個偽2-比特（pseudo 2-bits）中心頻率的移動。測量得到的濾波器響應示于圖4（b）中，其中通帶可以在四個不同的中心頻率處進行重構。

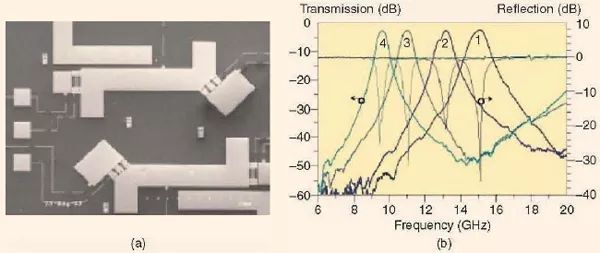
圖4、（a）一個2-比特射頻微機電系統可重構濾波器的照片和（b）它所測得的響應[11]。

文獻[13]中報道了在差分4-比特射頻微機電系統可調諧濾波器方面所進行的開創性的工作。這個濾波器展示出極其微細的調諧精度，可在6.5 到10GHz 之間進行寬調諧范圍的濾波，具有16 個頻率上彼此相鄰的不同的濾波響應，類似于一個連續可調諧濾波器。要了解更多有關射頻微機電系統可重構濾波器的信息，請參考本雜志中專注于這個論題的文章[16]。

壓電傳感器可調諧濾波器

壓電傳感器（PET）也已經同樣被用來開發電調微帶線濾波器[17]-[19]。圖5 對一個PET 可調諧微帶線濾波器的構建進行了說明。正如在文獻[17]中所報道的，這個可調諧濾波器電路包含有采用級聯微帶線開環諧振器[20]所組成的濾波器，一個PET 和一個在濾波器上方所附著的一個電介質微擾器。PET 是由鉛（lead），鋯酸鹽(Zirconate)和鈦酸鹽(Titanate)組成的。圖5 所示的PET是由兩個壓電層和一個墊片層組成的。夾在兩個同樣極化的壓電層之間的墊片層增加了機械強度和硬度。墊片連接到直流電壓的一個電極上來使PET 發生偏移，并且使之上下垂直運動。正如我們在圖5 的結構中所能看到的，當微擾器上下運動時，濾波器的有效介電常數便會分別降低或增加，從而使得濾波器的通帶向較高頻率或較低頻率處移動。

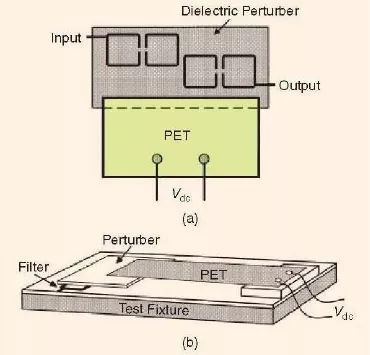
圖5、可調諧帶通濾波器的構建[17]。（a）頂視圖。（b）三維視圖。

可重構UWB?濾波器

具有可切換陷波的UWB濾波器

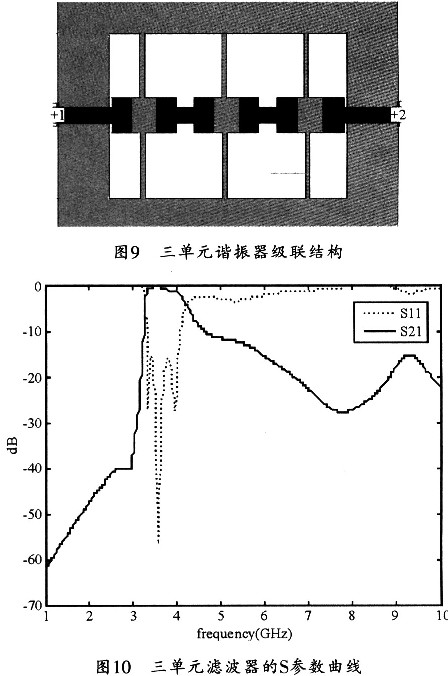
圖6 是所開發的具有可切換陷波頻段的UWB 帶通濾波器的圖片[24]。從根本上說，沒有陷波的UWB 濾波器是一個最佳的分布式高通濾波器，它在微帶線上含有5段短路截線和四段連接線段[1]。

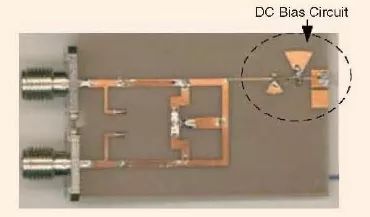
圖6、具有兩個可切換陷波結構的微帶線UWB 濾波器[24]。

為了在UWB 濾波器的通帶上實現一個可切換的陷波，如圖7 所示。兩個完全相同的可切換陷波結構被集成進入兩條連接線段中。這個結構中增加了一個寬帶直流偏置電路。從原理上講，圖7 中的可切換陷波結構是一段具有一個鑲嵌截線的傳輸線[39]。當p-i-n 二極管處于零偏置狀態時，由于其非常小的結電容而呈現出一個很大的阻抗，因此鑲嵌截線的作用便是一個可以產生諧振的開路截線。因此，在其基頻諧振頻率上，鑲嵌的開路截線在主傳輸線上顯示出短路的特性，從而產生一個窄的陷波頻段或者說是頻率響應中的陷波。這種情況對應的是陷波接通的狀態。為了關閉陷波，一個正向偏置被施加到p-i-n 二極管上。在正向偏置下，p-i-n 二極管相當于一個很小的電阻。因此，鑲嵌截線的開路端是與主傳輸線相連的，從而，沒有來自于這個鑲嵌截線的諧振。因此，陷波便會消失。

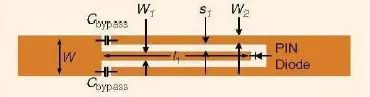
圖7、一個可切換陷波結構的示意圖[24]。

圖8 展示了可重構UWB 濾波器仿真和測量的響應，其中，我們可以觀察到在中心頻率約為5.1GHz 處的陷波的接通/關閉，當其接通時，其抑制比大于35dB。為了接通陷波，p-i-n 二極管（M/A-COM MA 4AGSBP907）是處于零偏置狀態。當關閉陷波時，濾波器的性能與當p-i-n 二極管處于2.5-5mA 的正向偏置狀態下的性能來說幾乎是一樣的。所測得的最小插入損耗為0.5dB，并且測量得到的3dB 帶寬為5.92GHz。仿真和測量結果之間很小的差異可以解釋為是由制造公差，p-i-n 二極管，芯片電感或電容的雜散效應所引起的。

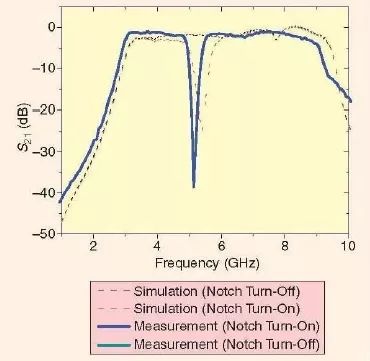
圖8、仿真和測量結果的比較[24]。（電磁(EM)仿真是使用商業化的工具得到的[40]。）

具有可調諧陷波的UWB?濾波器

在圖6 中，人們用變容二極管來替代p-i-n 二極管便可以產生一個可調諧陷波結構。因此，前面所討論的可重構UWB 濾波器可以進行修改，從而具有一個可進行電子調諧的陷波頻段。所采用的是M/A-COM 公司的具有恒定伽瑪值的GaAs 倒裝芯片變容二極管[25]。圖9（a）展示了MA46H120 變容二極管典型的性能曲線。為了進行實驗演示，具有可調諧陷波的UWB 濾波器是在液晶聚合物上（LCD）實現的，基片的相對介電常數為3.0，厚度為0.5mm。圖9(b)是所制作的濾波器。除了用變容二極管來替代p-i-n 二極管外，其版圖設計與圖6 的類似。變容二極管是通過一個10kΩ 電阻與直流電壓相連接的。

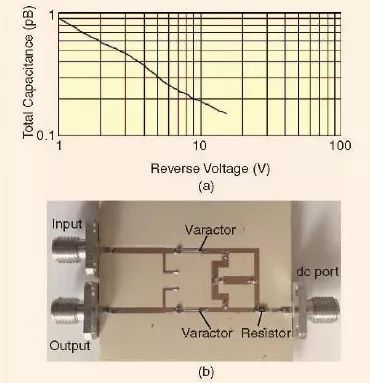
圖9、（a）MA46H120 變容二極管典型的性能。（b）采用MA46H120 變容二極管所制作的具有可調諧陷波的可重構超寬帶濾波器[25]。

圖10 是所測得的可重構UWB 濾波器的響應。當沒有直流偏置時（0V），在通帶上沒有陷波，如圖10（a）所示。這是因為變容二極管電容在0-V 偏置下是如此之大，以至于它將陷波頻段移動到了通帶以下。當直流偏置在4V 到14V 時，陷波頻率在UWB 通帶內4.5GHz 到6.5GHz 范圍內被調諧，如圖10（b）所示。

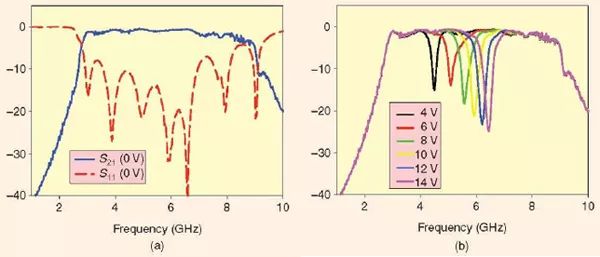
圖10、具有可調諧陷波頻段的可重構超寬帶濾波器所測得的性能。（a）沒有陷波的0-V 偏置。（b）具有可調諧陷波的非零偏置（來源于[25]）。

具有槽線接地結構的BST?變容器調諧帶阻濾波器

諸如BST 這類鐵電體材料新近在用于頻率捷變應用的電調微波電路的開發中變得更加吸引人[41]-[42]。接下來，我們要介紹最新開發的BST 變容器可調諧帶阻濾波器[28]。

BST?變容器

BST 變容器的電容可調諧能力可以定義為

電容可調諧能力=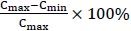?(1)

其中Cmax是BST 變容器在0-V 偏置下的電容，Cmin?是在非零直流偏置下所獲得的電容。當直流偏置電壓的絕對值提高時，Cmin?會有所降低，這是因為BST 材料的相對介電常數是隨著所施加的電壓而減小的[42]。

一般來說，BST 變容器可以設計成金屬-絕緣體-金屬電容器的形式，或一種叉指電容器（IDC）的形式。BST 可調諧IDC 由于其額外的對直流電壓不甚敏感的邊緣電容而具有較小的電容可調諧能力。圖11 說明了BST IDC 典型的特性[2]，當要求具有較低的電容值以及比較簡單的制造工藝時，BST 可調諧IDC 便是一個更具有吸引力的選擇。

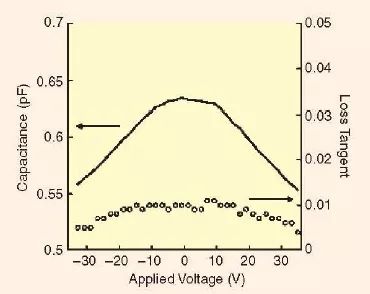
圖11、鈦酸鍶鋇叉指電容變容器在1MHz 下的標稱調諧曲線（有20 個叉指，每個叉指寬為5μm，長為100 μm，叉指間距為5μm）[2]。

正如在文獻[28]中所公布的，IDC BST 變容器是在圖12（a）所示結構的基礎上制作的。通過脈沖激光沉積法將一層0.5-μm 厚的Ba0.5Sr0.5TiO3?（BST）薄膜沉積到一個（001）MgO 基片上（厚度為0.5-mm），在有氧環境下（0.1mbar）采用具有1.5Jcm-2?的激光以5Hz 的注入脈沖速度進行沉積[42]。所制成的BST 材料在電場強度從3.5 變化到0V/μm 時，相對介電常數從700 變化到1,200，所測得的BST 薄膜的介電損耗tanδ 在10MHz 下從0.1 變化到0.2。

圖12（b）展示了具有六個叉指的IDC，這是文獻[28]中所開發的BST 變容器的基本單元。彼此間距為10μm 的叉指為220-μm 長，10-μm寬。這個基本BST 變容器單元在0-V 偏置下的Cmax=0.56pF，在35-V 偏置下的Cmin=0.4pF，根據式（1），它在給定的直流偏置電壓范圍中的電容可調能力為28.6%。為了實際應用起見，人們制作了一個大的BST 變容器芯片，這個芯片可以很容易地附著在傳統的微波電路板上。其尺寸為5×5mm2，含有三個并聯的BST 變容器單元。

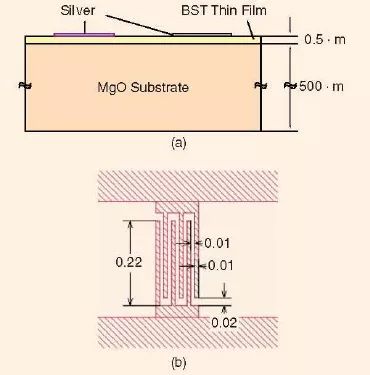
圖12、（a）在MgO 基片上所制作的鈦酸鍶鋇叉指變容器芯片的剖面層。（b）鈦酸鍶鋇叉指變容器單元的版圖（尺寸單位為mm）[資料來源于28]。

可調諧帶阻濾波器

圖13 展示了一個具有槽線接地結構的兩極點可調諧帶阻濾波器。在接地平面上，可調諧微帶線帶阻濾波器包含兩個可調諧BST 槽線諧振器和向BST 變容器提供直流電壓的偏置電路。

圖13、制作成的采用鈦酸鍶鋇變容器的可調諧微帶線帶阻濾波器[28]。（a）底部和（b）頂部。

圖14 給出了可調諧微帶線帶阻濾波器的測量響應；這個帶阻濾波工作在中心頻率為1.2-1.4GHz 處，具有100MHz 的帶寬。因此，所測得的調諧范圍是14%。

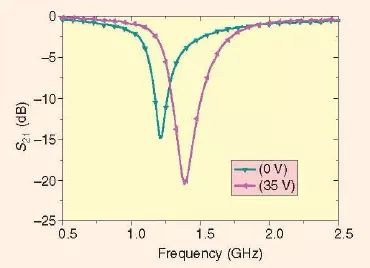
圖14、可調諧帶阻濾波器的測量結果[28]。

可重構雙模帶通濾波器

人們可以在單模或雙模諧振器的基礎上設計帶通濾波器，并且傾向于在微帶線上進行設計，因為直流偏置電路可以很容易地在微帶線上實施。雙模微帶線諧振器是很有吸引力的，因為每個雙模諧振器可以被用作雙調諧諧振電路，因此，給定了階數的濾波器所需的諧振器的數量可以減半，從而可以產生一個緊湊的濾波器架構。對于一個傳統的雙模濾波器來說，兩種簡并的模式是通過控制一個合適的擾動而進行耦合的。環形濾波器（Circular ring filter）[43]，方形環路濾波器（Square loop filter），以及彎折環路濾波器（meander loop filter）[45]便屬于這種情況。另一方面，在文獻[46]中人們研究了一種新型的基于三角形貼片基礎之上的雙模諧振器濾波器，其中并未對雙模進行耦合。最近，人們已經在一個小型的雙模微帶線開環濾波器中展示了這種獨特且有趣的特性[47]，這種諧振器是由傳統的單模開環諧振器演變而來的[20]。

當具有兩維對稱性的傳統雙模諧振器被用于雙模帶通濾波器的設計之中時，需要一些擾動來將兩種簡并的模式分開[1]。而在文獻[46]和[47]中所介紹的雙模諧振器則并不需要這個擾動，因為其兩種分別被稱為偶模和奇模的諧振模式彼此并不相互耦合。這兩種模式會在雙模濾波器中分開的頻率上工作，其耦合結構是與傳輸的雙模濾波器的耦合結構有所不同的。圖15 展示了這種類型的一個兩極點雙模濾波器的耦合結構，其中S 和L分別代表著輸入和輸出端口；節點1 代表著奇模，節點2 代表著偶模。文獻[46]和[47]中演示了具有固定中心頻率的這種類型的濾波器。

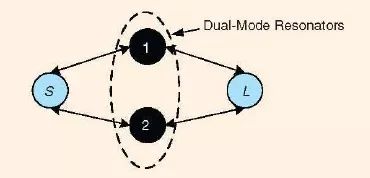
圖15、一個兩極點雙模濾波器的耦合結構，其中這兩個模式彼此之間是沒有耦合的[35]。

在文獻[34]-[36]中，人們同樣研究了電子可重構雙模微帶線開環諧振器濾波器，這種濾波器發掘了在單個雙模諧振器中的兩個諧振模式之間無耦合的獨特特性。這便產生了一個簡單的調諧方案，因為通帶頻率的調諧僅僅通過按比例改變模態頻率便可完成。此外，對于這種類型的濾波器來說，其選擇性可以通過電子方式重新設置，從而在通帶的任何一邊都會展示出具有一個有限頻率傳輸零點的較高的選擇性。

具有兩個直流偏置的可重構雙模濾波器

正如在文獻[34]中所討論的，圖16 所顯示的是制作成的兩極點可重構雙模微帶線開環諧振器帶通濾波器。

圖16、制作成的具有兩個直流偏置的可重構雙模微帶線開環諧振器帶通濾波器[34]。

這個帶通濾波器具有如圖15 所示的耦合方案。由于在兩種工作諧振模式之間不存在耦合，因此，如果奇模和偶模的諧振頻率是按比例移動的話，便可以調諧通帶的中心頻率。人們所采用的典型的可變電容在0.5pF到6.6pF 之間變化的Infineon BB857 變容器來實施這種電子調諧。為了能重構濾波器的特性，人們采用了兩個直流偏置。第一個直流偏置電壓V1?被用來改變奇模頻率，第二個直流偏置電壓V2被用來改變偶模頻率。

測量得到的頻率響應繪制在圖17 中，這個頻率響應展現出，取決于兩個直流偏置的組合情況，人們不僅可以調諧通帶頻率，而且濾波特性也同樣可以重構，從第一種情況下的通帶高頻一邊具有高的選擇性而改變為第二種情況下，通帶的低頻一邊具有高的選擇性。

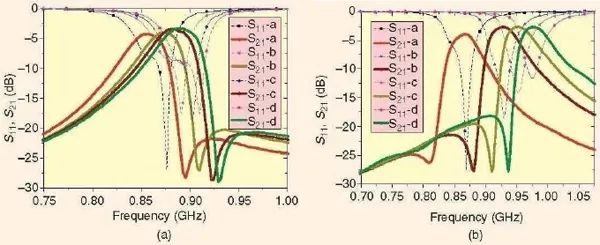
圖17、具有兩個直流偏置的可重構雙模濾波器的測量性能。（a）第一種情況。（b）第二種情況[34]。

具有單個直流偏置的可調諧雙模濾波器

通過改變雙模微帶線開環諧振器，雙模濾波器的中心頻率可以通過采用單個直流偏置來進行電子調諧。換句話說，偶模和奇模諧振頻率的改變由于使用同樣的偏置電壓而變得更為簡便。圖18（a）展示了這種可調諧濾波器的一個例子[35]。這個濾波器是在相對介電常數為10.8 且厚度為1.27mm 的基礎上制作的。這個濾波器上連接了三只Infineon BB857 變容器，這與上一種情況類似。變容器饋入的是同樣的直流偏置電壓。圖18（b）展現出當直流偏置電壓從8.1V 變化到25V 時所測得的頻率響應。這個濾波器在通帶的高端處展現了一個有限頻率的傳輸零點，其中心頻率的調諧范圍是100MHz，在825 到925MHz 之間。在這種情況下，在濾波器進行調諧時，偶模頻率總是高于奇模頻率[46]。

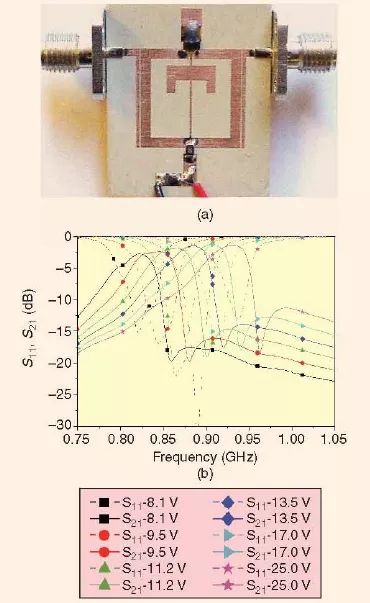
圖18、（a）制作成的采用單個直流偏置，在通帶高端處含有一個有限頻率傳輸零點的可調諧雙模濾波器。（b）所測得的頻率響應[35]。（ 圖片版權European Microwave Association，EuMA。經許可使用。）

人們還可以采用另一種修改方案，文獻[35]便展示了用單個直流偏置進行調諧，在通帶的低端處具有一個有限頻率的傳輸零點的可調諧雙模濾波器。

可調諧四極點雙模濾波器

可以將兩個或多個雙模，開環諧振器進行級聯來構建一個具有較高階數的可調諧濾波器。例如，圖19 顯示了一個制作成的這種類型的四極點可調諧濾波器[36]。每個雙模開環諧振器加載了三個Infineon BB857 變容器。整個濾波器是用單個直流偏置電路來調諧的。直流偏置在10.6V 到34.0V 的范圍內變化時的測量結果繪制在圖20 中，并與加載了不同的變容器電容值的仿真結果進行了比較。

圖19、制作成的四極點可調諧雙模濾波器[36]。（圖片版權European Microwave Association，EuMA。經許可使用。）

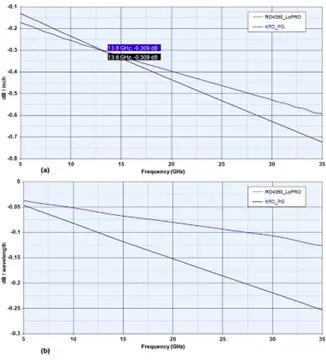
圖20 展示了實驗用四極點可調諧帶通濾波器在通帶的每一邊都具有一個有限頻率傳輸零點的準橢圓函數響應。接近于通帶低端處的傳輸零點是與第一個雙模諧振器所固有的偶模相關聯的，而靠近通帶高端處的傳輸零點則是與第二個雙模諧振器的偶模相關聯的。因此，當偶模頻率被調諧時，相關的傳輸零點也會作出相應的移動。對于給定的直流偏置電壓范圍，人們可以在0.86-0.96GHz 的調諧范圍內對濾波器進行調諧。

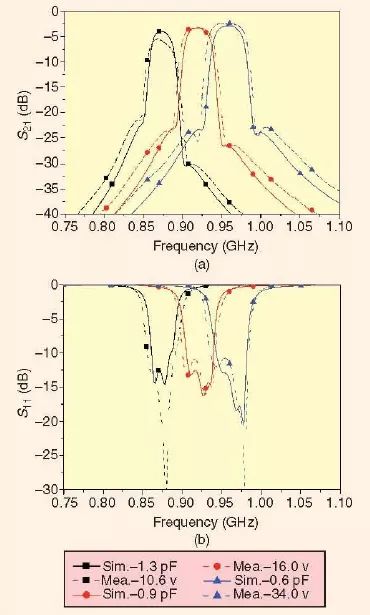
圖20、測量得到的可調諧濾波器的性能與仿真結果的比較。（a）S21 和（b）S11 [36]。

結論

本文介紹了若干種電子可重構或可調諧微帶線濾波器。通過采用不同的電子控制技術，包括射頻微機電系統和鐵電體，梳狀濾波器結構已經被廣泛地用來開發可調諧或可重構濾波器，雖然這類濾波器的帶寬通常都很小。本文所展示的UWB 濾波器采用的是p-i-n 二極管，但人們還實施了其它可切換元件，如金屬半導體場效應管（MESFET）開關。MESFET 開關具有較低的直流功耗，但都有較大的非線性失真。人們同樣還可以考慮使用射頻微機電系統[13]-[14]或PET[18]。

BST 變容器已被用于具有槽線接地結構的電調微帶線帶阻濾波器中。這些結構可以很方便地實施調諧元件和直流偏置電路，使之與基片另一面的主要射頻信號路徑具有更好的隔離性。鐵電體薄膜調諧器件，如BST 變容器在較高頻率應用中是很有吸引力的，雖然其損耗需要被減到最小程度。

我們已經展示出一個可以通過控制奇模和偶模的諧振頻率這種簡單方式來調諧或者說進行電子重構的雙模微帶線開環諧振器濾波器，因為這兩種操作模式彼此之間不存在耦合。

除了半導體變容器外，人們還實施了其它類型的變容器和技術，如鐵電體薄膜和射頻微機電系統變容器。一個類似的調諧技術可以被應用于較高階數的濾波器中，在一個具有準橢圓函數響應的電調四極點雙模微帶線開環諧振器濾波器中已經演示了這種技術。通過選擇合適的變容二極管并且合理地設計輸入和輸出饋電結構，便可以提高頻率調諧范圍。采用額外的調諧元件來控制輸入和輸出耦合，對濾波器帶寬進行調諧也同樣是可行的。

總的來說，帶寬的調諧或控制比頻率的調諧更加具有挑戰性，具有較大帶寬的電調濾波器的設計就調諧范圍和帶寬控制來說比窄帶寬的更加困難。文獻[48]-[51]中報道了一些在可調諧濾波器中進行帶寬控制的技術。

電子可重構濾波器的非線性行為非常依賴于所使用的調諧元件。采用射頻微機電系統和PET 通常會產生一個較好的線性特性。可重構濾波器設計中的創新同樣可以改善性能并且能增加功能。調諧元件相對較低的Q 值會限制較高階數和窄帶可調諧濾波器的實施。這是因為，對于給定Q 值的調諧元件和其它與電路相關聯的損耗來說，濾波器的插入損耗是隨著其階數的增高和帶寬的降低而增加的。因此，高階可調諧窄帶濾波器的插入損耗對于實際應用來說是太大了。此外，調諧范圍在高階濾波器的限制比低階濾波器的限制更大[4]。

可重構濾波器的開發涉及到一些折衷之處，例如濾波器的尺寸和偏置電路的復雜性，這些都增加了挑戰性。可以設想在開發電子可重構微帶線濾波器方面將會有更多的研究和開發活動。有眾多文獻都涉及到這個論題，其中一些被列入參考文獻之中，感興趣的讀者可以參考這些文獻以獲取跟多的資訊。

致謝

本文所介紹的一些工作是由U.K.Engineering and Physical Science Research Council 通過兩個研究項目（EP/C520289/1 ）和（EP/E02923/1）給予資助的。作者對參與這些項目的組織和個人表示感謝。

參考文獻

[1] J.-S. Hong and M. J. Lancaster, Microstrip Filters for RF/Microwave Applications. New York: Wiley, 2001.
[2] J. Nath, D. Ghosh, J.-P. Maria, A. I. Kingon, W. Fathelbab, P. D. Franzon, and M. B. Steer, “An electronically tunable microstrip bandpass filter using thin-film barium-strontium-titanate (BST) varactors,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 9, pp.2707–2712, Sept. 1982.
[3] J. Sigman, C. D. Nordquist, P. G. Clem, G. M. Kraus, and P. S. Finnegan, “Voltage-controlled Ku-band and X-band tunable combline filters using barium-strontium-titanate,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 9, pp. 593–595, Sept. 2008.
[4] I. Vendik, O. Vendik, V. Pleskachev, A. Svishchev, and R. Wordenweber, “Design of tunable ferroelectric filters with a constant fractional band width,” in IEEE MTT-S Int. Microwave Symp. Dig., May 2001, vol. 3, pp. 1461–1464.
[5] W. M. Fathelbab and M. B. Steer, “A reconfigurable bandpass filter for RF/microwave multifunctional systems,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 3, part 2, pp. 1111–1116, Mar. 2005.
[6] G. Torregrosa-Penalva, G. Lopez-Risueno, and J. I. Alonso, “A simple method to design wide-band electronically tunable combline filters,” IEEE Trans. Microwave Theory Tech., vol. 50, no. 1, part 1, pp.172–177, Jan. 2002.
[7] I. Vendik, O. Vendik, V. Pleskachev, and M. Nikol’ski, “Tunable microwave filters using ferroelectric materials,” IEEE Trans. Appl. Superconduct., vol. 13, no. 2, part 1, pp. 716–719, June 2003.
[8] B.-W. Kim and S.-W. Yun, “Varactor-tuned combline bandpass filter using step-impedance microstrip lines,” IEEE Trans. Microwave Theory Tech., vol. 52, no. 4, pp. 1279–1283, Apr. 2004.
[9] M. Sanchez-Renedo, “High-selectivity tunable planar combline filter with source/load-multiresonator coupling,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 7, pp. 513–515, July 2007.
[10] G. M. Kraus, C. L. Goldsmith, C. D. Nordquist, C. W. Dyck, P. S. Finnegan, F. Austin, IV, A. Muyshondt, and C. T. Sullivan, “A widely tunable RF MEMS end-coupled filter,” in 2004 IEEE MTT-S Int. Microwave Symp. Dig., June 6–11, 2004, vol. 2, pp. 429–432.
[11] P. Blondy, C. Palego, M. Houssini, A. Pothier, and A. Crunteanu, “RFMEMS reconfigurable filters on low loss substrates for flexible front ends,” in Proc. Asia-Pacific Microwave Conf. 2007 (APMC 2007), Dec. 11–14, 2007, pp. 1–3.
[12] A. Pothier, J.-C. Orlianges, G. Zheng, C. Champeaux, A. Catherinot, D. Cros, P. Blondy, and J. Papapolymerou, “Low-loss 2-bit tunable bandpass filters using MEMS dc contact switches,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 1, pp. 354–360, Jan. 2005.
[13] K. Entesari and G. M. Rebeiz, “A differential 4-bit 6.5-10-GHz RF MEMS tunable filter,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 3, part 2, pp. 1103–1110, Mar. 2005.
[14] I. C. Reines, C. L. Goldsmith, C. D. Nordquist, C. W. Dyck, G. M. Kraus, T. A. Plut, P. S. Finnegan, F. Austin, IV, and C. T. Sullivan, “A low loss RF MEMS Ku-band integrated switched filter bank,” IEEE Microwave Wireless Compon. Lett., vol. 15, no. 2, pp. 74–76, Feb. 2005.
[15] R. Zhang and R. R. Mansour, “Novel tunable lowpass filters using folded slots etched in the ground plane,” in 2005 IEEE MTT-S Int. Microwave Symp. Dig., June 12–17, 2005, pp. 775–778.
[16] G. M. Rebeiz, K. Entesari, I.C. Reines, S.-J. Park, M.A. El-Tanani, A. Grichener, and A.R. Brown, “Tuning in to RF MEMS,” IEEE Microwave Mag., vol. 10, no. 6, pp. 55–72, Oct. 2009.
[17] L.-H. Hsieh and K. Chang, “Tunable microstrip bandpass filters with two transmission zeros,” IEEE Trans. Microwave Theory Tech., vol. 51, no. 2, part 1, pp. 520–525, Feb. 2003.
[18] W.-T. Tu and K. Chang, “Piezoelectric transducer-controlled dualmode switchable bandpass filter,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 3, pp. 199–201, Mar. 2007.
[19] Y. Poplavko, D. Schmigin, V. Pashkov, M. Jeong, and S. Baik, “Tunable microstrip filter with piezo-moved ground electrode,” in Proc. 2005 European Microwave Conf., Oct. 4–6, 2005, vol. 2.
[20] J.-S. Hong and M. J. Lancaster, “Couplings of microstrip square openloop resonators for cross-coupled planar microwave filters,” IEEE Trans. Microwave Theory Tech., vol. 44, no. 11, pp. 2099–2109, Nov. 1996.
[21] S. Pal, C. Stevens, and D. Edwards, “Tunable HTS microstrip filters for microwave electronics,” Electron. Lett., vol. 41, no. 5, pp. 286–288, Mar. 2005.
[22] G. L. Matthaei, “Narrow-band, fixed-tuned, and tunable bandpass filters with zig-zag hairpin-comb resonators,” IEEE Trans. Microwave Theory Tech., vol. 51, no. 4, part 1, pp. 1214–1219, Apr. 2003.
[23] G. Subramanyam, F. W. Van Keuls, and F. A. Miranda, “A K bandfrequency agile microstrip bandpass filter using a thin-film HTS/ferroelectric/dielectric multilayer configuration,” IEEE Trans. Microwave Theory Tech., vol. 48, no. 4, part 1, pp. 525–530, Apr. 2000.
[24] Y.-H. Chun, H. Shaman, and J.-S. Hong, “Switchable embedded notch structure for UWB bandpass filter,” IEEE Microwave and Wireless Compon. Lett., vol. 18, no. 9, pp. 590–592, Sept. 2008.
[25] H. R. Arachchige, J.-S. Hong, and Z.-C. Hao, “UWB bandpass filter with tunable notch on liquid crystal polymer substrate,” in Proc. Asia-Pacific Microwave Conf. 2008 (APMC 2008), Dec. 16–20, 2008, pp. 1–4.
[26] E. E. Djoumessi, M. Chaker, and K. Wu, “Varactor-tuned quarterwavelength dual-bandpass filter,” IET Microwaves, Antennas Propagat., vol. 3, no. 1, pp. 117–124, Feb. 2009.
[27] D. R. Jachowski, “Compact, frequency-agile, absorptive bandstop filters,” in IEEE MTT-S Int. Microwave Symp. Dig., 2005, pp. 513–516.
[28] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “BST varactor tuned bandstop filter with slotted ground structure,” in Proc. 2008 IEEE MTT-S Int. Microwave Symp., June 2008, pp. 1115–1118.
[29] S. Y. Huang and Y. H. Lee, “A compact e-shaped patterned ground structure and its applications to tunable bandstop resonator,” IEEE Trans. Microwave Theory Tech., vol. 57, no. 3, pp. 657–666, Mar. 2009.
[30] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “An electronically tuned bandstop filter using BST varactors,” in Proc. 38th?European Microwave Conf. 2008, EuMC 2008, Oct. 27–31, 2008, pp. 1699– 1702.
[31] W. D. Yan and R. R. Mansour, “Compact tunable bandstop filter integrated with large deflected actuators,” in Proc. 2007 IEEE/MTT-S Int. Microwave Symp., June 3–8, 2007, pp. 1611–1614.
[32] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “BSTvaractor tunable dual-mode filter using variable ZC transmission line,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 3, pp. 167–169, Mar. 2008.
[33] M. R. Al Mutairi, A. F. Sheta, and M. A. AlKanhal, “A novel reconfigurable dual-mode microstrip meander loop filter,” in Proc. 38th European Microwave Conf. 2008, EuMC 2008, Oct. 27–31, 2008, pp. 51–54.
[34] Y.-H. Chun and J.-S. Hong, “Electronically reconfigurable dualmode microstrip open-loop resonator filter,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 7, pp. 449–451, July 2008.
[35] W. Tang and J.-S. Hong, “Compact tunable microstrip bandpass filters with asymmetrical frequency response,” in Proc. 38th European Microwave Conference (EuMC2008), pp. 599–602.
October 2009 IEEE microwave magazine 83
[36] W. Tang and J.–S. Hong, “Tunable microstrip quasi-elliptic function bandpass filters,” in Proc. 39th European Microwave Conf., 2009, Paper EuMC41-1.
[37] P. W. Wong and I. C. Hunter, “A new class of low-loss high-linearity electronically reconfigurable microwave filter,” IEEE Trans. Microwave Theory Tech., vol. 56, no. 8, pp. 1945–1953, Aug. 2008.
[38] P.W. Wong and I. Hunter, “Electronically tunable filters,” IEEE Microwave Mag., vol. 10, no. 6, pp. 46–54, Oct. 2009.
[39] H. Shaman and J.-S. Hong, “Ultra-wideband (UWB) bandpass filter with embedded band notch structures,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 3, pp. 193–195, Mar. 2007.
[40] EM User’s Manual, Version 10, Sonnet Software Inc., NY, 2006.
[41] F. A. Miranda, G. Subramanyam, F. W. van Keuls, R. R. Romanofsky, J. D. Warner, and C. H. Mueller, “Design and development of ferroelectric tunable microwave components for Ku and K-band satellite communication systems,” IEEE Trans. Microwave Theory Tech.,vol. MTT-48, no. 7, pp. 1181–1189, July 2000.
[42] P. M. Suherman, T. J. Jackson, Y. Y. Tse, I. P. Jones, R. I. Chakalova, and M. J. Lancaster, “Microwave properties of Ba0.5Sr0.5TiO3 thin film coplanar phase shifters,” J. Appl. Phys., vol. 99, no. 104101, pp. 1–7, May 2006.
[43] I. Wolff, “Microstrip bandpass filter using degenerate modes of a microstrip ring resonator,” Electron. Lett., vol. 8, no. 12, pp. 302–303, June 1972.
[44] J.-S. Hong and M. J. Lancaster, “Bandpass characteristics of new dualmode microstrip square loop resonators,” Electron. Lett., vol.31, no. 11, pp. 891–892, May 1995.
[45] J.-S. Hong and M. J. Lancaster, “Microstrip bandpass filter using degenerate modes of a novel meander loop resonator,” IEEE Microwave Guided Wave Lett., vol. 11, no. 5, pp. 371–372, Nov. 1995.
[46] J.-S. Hong and S. Li, “Theory and experiment of dual-mode microstrip triangular patch resonators and filters,” IEEE Trans. Microwave Theory Tech., vol. 52, no. 4, pp. 1237–1243, Apr. 2004.
[47] J.-S. Hong, H. Shaman, and Y. H. Chun, “Dual-mode microstrip open-loop resonators and filters,” IEEE Trans. Microwave Theory Tech., vol. 55, no. 8, pp. 1764–1770, Aug. 2007.
[48] W. L. Jones, “Design of tunable combline filters of near-constant bandwidth,” Electron. Lett., vol. 1, no. 6, pp. 156–158, Aug. 1965.
[49] B. E. Carey-Smith, P. A. Warr, M. A. Beach, and T. Nesimoglu, “Wide tuning-range planar filters using lumped-distributed coupled resonators,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 2, pp. 777–785, Feb. 2005.
[50] M. Sanchez-Renedo, R. Gomez-Garcia, J. I. Alonso, and C. Briso- Rodriguez, “Tunable combline filter with continuous control of center frequency and bandwidth,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 1, pp. 191–199, Jan. 2005.
[51] M. Sanchez-Renedo and R. Gomez-Garcia, “Small-size planar tunable combline filter using decoupling walls,” Electron. Lett., vol. 43, no. 9, pp. 532– 534, Apr. 2007.

編輯：黃飛

?