關于傅立葉變換，無論是書本還是在網上可以很容易找到關于傅立葉變換的描述，但是大都是些故弄玄虛的文章，太過抽象，盡是一些讓人看了就望而生畏的公式的羅列，讓人很難能夠從感性上得到理解，對于這個有史以來最重要的發現之一。如何才能更輕易地理解這個公式呢？

　　

　　

　　那么。拋開枯燥難懂的數學符號，讓我們用一種新方法來試著理解。這是一個純中文的闡述：

　　傅立葉變換有什么用？拿一杯思暮雪，用它能找出配方。

　　該怎么做呢？把思暮雪放進過濾器（濾波器），然后萃取每一種成分。

　　為什么呢？因為配方比思暮雪本身更容易用來分析、比較和定義。

　　我們怎么能拿回原本的思暮雪呢？混合所有的成分。

　　然后，類似于“數學-中文”模式：

　　基于時域的傅立葉變換會檢測每一種“周期成分”（周期長度，補償，和轉速），返回完成的“周期配方”（頻率圖譜）

　　現在要上公式了？當然不是！讓我們自己動手，進行一次生動的模擬。

　　要是一切順利的話，你會驚奇的發現，你已經直觀的明白了為什么傅立葉變換能夠實現。我們用下列步驟替代了所有的數學分析。

　　這并不是一次緊張的實驗，而是一次舒心的體驗。讓我們開始吧！

　　由思暮雪得到配方

　　數學變換的實質是變量關系的改變。根據所算之物，把我們對數量的認知從“單一物體”（沙里的線條，計數系統）變成“許多10”（小數）。游戲得分？繼續計數。乘法？拜托，是小數。

　　傅立葉變換把我們的視角由消費者變成了生產者，從“我看到了什么？”變成“這是怎么發生的？”。

　　換句話說：拿一個思暮雪，我們要找出它的配方。

　　為什么呢？好吧，配方是飲料的最佳描述。你并不會跟人一滴一滴分析飲料，只會說“我有一杯橘子或是香蕉思暮雪”。配方比事物本身更易于歸類、比對和定義。

　　那么……拿一杯思暮雪，到底怎么找到配方呢？

　　

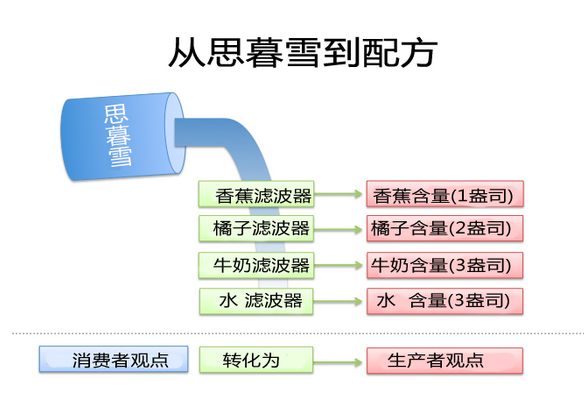
　　嗯，想象一下你周圍有很多過濾器（濾波器）：

　　把思暮雪倒進“香蕉”過濾器（濾波器）里。提取出了1盎司香蕉。

　　倒進“橘子”過濾器（濾波器）里。提取出了2盎司橘子。

　　倒進“牛奶”過濾器（濾波器）里。提取出了3盎司牛奶。

　　倒進“水”過濾器（濾波器）里。提取出了3盎司水。

　　我們可以通過混合每種成分得到原先的思暮雪。懂了么？

　　過濾器（濾波器）必須是相互獨立的。香蕉過濾器（濾波器）只濾出香蕉，沒有其它的任何成分。再多的橘子也不能影響香蕉的讀數。

　　過濾（濾波）必須是徹底的。如果我們遺漏了一個過濾器（濾波器），就永遠也得不到真正的配方（天哪！那還有個芒果過濾器（濾波器）！）。我們的過濾器（濾波器）必須能確定每種成分的含量。

　　不同成分之間必須是可合成的。思暮雪必須能被分離并重制（餅干？沒那么夸張。誰有想要一堆碎屑呢？）。不同成分在分離和結合的時候必須是線性的。

　　周期看世界

　　傅立葉變換持有一種特別的觀點：要是每一種信號都是周期性的呢（周期性重復）？

　　哇塞。這個假設太讓人著迷了，可憐的約瑟夫·傅立葉首先提出了這個假設。（現實里約瑟夫，樓梯能做成環狀的么？）

　　忽略數學界持續數十年的爭論，我們希望學生們可以直觀的理解這個概念。額……讓我們略過直觀的部分。

　　就像我們分析思暮雪成分一樣，傅立葉變換可以分析出信號的成分：

　　開始時，是一個時域信號

　　用濾波器來測定每種可能的“周期信號成分”

　　完整的“配方”需要列出所有的“周期信號成分”的數值

　　完成。這就是大部分教程要教給你的東西。別被嚇到了；想想這個例子“天哪，過五關斬六將，我們終于得到源代碼（DNA）了”。

　　要是地震波（不同強度和速度的震動）能被分離成幾種成分，建筑就能被設計成免于地震威脅的高強度結構。

　　要是聲波（高低不同的頻率）能被分成幾種成分，我們就能增強想要的部分，削弱不想要的部分。隨機噪聲引起的噼啪聲可以被濾除。相似的“聲譜”可以被比對（音樂識別服務比對的是聲譜而不是原始音頻）。

　　要是電腦數據能被周期性的描述，那些不重要的信息就能被濾除。這種“有損壓縮”可以急劇減小文件的大小（這就是為什么JPEG和MP3文件要比原始的.bmp或.wav文件要小得多的原因）。

　　要是我們的信號是無線電波，我們可以通過濾波器來聽確定的頻段。在思暮雪的世界里，想象每個人都注意著不同的成分：亞當在尋找蘋果，鮑勃在尋找香蕉，查理想要花椰菜（兄弟，對不住了）。

　　傅立葉變換在工程領域運用廣泛，但事實上，它是個尋找現象根源的象征。

　　多想想周期信號，而不是正弦曲線

　　我最大的困惑在于“正弦曲線”和“周期信號”的定義區分。

　　“正弦曲線”意味一種往復運動模式（正弦或余弦函數）。在99%的場合里，指的都是發生在象限里的運動

　　周期信號是一種環形，包括兩個D形圖案的模式。要你愿意用10塊錢的話來描述10分錢的主意，你可以把一個圓形路徑稱作一個“完整正弦曲線”。

　　把一個周期的路徑稱作一個“完整正弦曲線”，就像你把一個諺語叫做“漢字的集合”。你選擇了錯誤的細節級別。諺語包含了復雜的含義，而不是可以拆分的漢字！

　　傅立葉變換是關于周期（不是含有一個D形的正弦曲線）和歐拉公式的變換：

　　

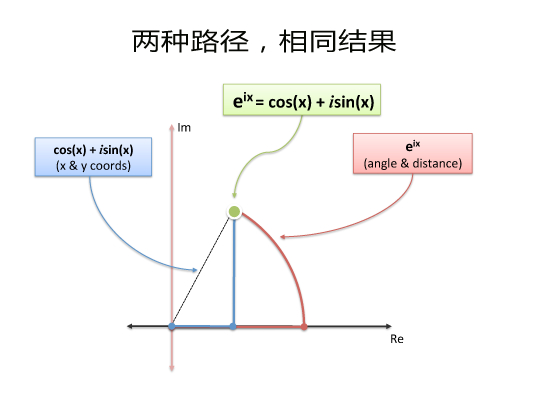
　　我們必須用虛數做周期運動么？當然不。即使那么做既方便又簡潔。我們把信號分成實數和虛數的部分，但別忘了前提是：我們在做周期運動。

　　沿著周期路徑

　　我們一邊用電話聊天，一邊在腦海里畫圓（你答應了的！）。我該說什么呢？

　　這個圈兒該有多大呢？（幅度，半徑范圍的大小）

　　我們要畫得多快？（頻率。1周期/秒=1赫茲=2π弧度/秒）

　　從哪里開始呢？（相位角，0度對應x軸）

　　我可以說“2英寸，起始于45度，1圈兒每秒，開始吧！”。半秒之后，我們應該到達了同一點：起始位置+經過角度=45+180=225度（2英寸半徑）。

　　

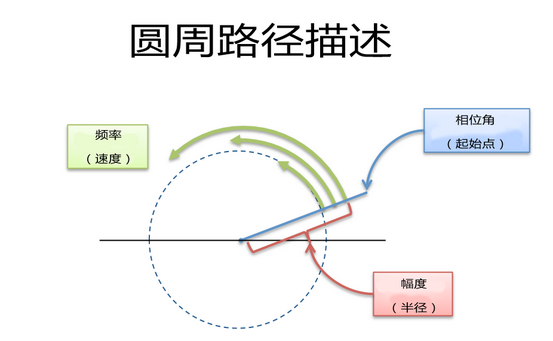
　　每個圓周路徑都需要設定大小、速度和起始角度（幅度/周期/相位）。我們還可以把它們合到一塊：想象用不同速度繞圈兒跑的小摩托車。

　　所有周期的位置信息加到一起就是原本的信號，一如所有的成分混合就得到了原本的思暮雪一樣。

　　下面是一個對基本圓周路徑的仿真：

　　（詳細、直觀的動畫。需要瀏覽器。點擊圖像暫停/繼續。）

　　周期的時間順序顯示，開始于0Hz。周期［0 1］的含義是

　　0的意思是0Hz周期（0Hz=開始于x軸，0度相位的連續周期）

　　1的意思是1Hz周期（每個時間間隔完成一個周期）

　　現在是棘手的部分：

　　藍色圖像表示周期的實數部分。另一個可愛的數學問題：我們常用水平軸來表示每個周期的實軸，其數值在數值軸上顯示。你也可以把坐標軸旋轉90度。

　　時間點間隔按照最高頻率設定。1Hz信號需要兩個時間點來表示，分別記錄起始和終止時刻（一個信號值是沒有頻率的。）。時間值［1 -1］對應著這些等間隔點的幅度。

　　然后呢？［0 1］是1Hz周期。

　　現在加入2Hz周期，并疊加。［0 1 1］意味著“0Hz值為零，1Hz時值為1，2Hz時值為1”：

　　哇塞。我們的小摩托車越跑越快了：綠線代表了1Hz和2Hz，藍線是疊加后結果。點選綠色復選框可以讓結果看起來更清晰。混合好的“味道”是一個傾斜的函數，從最大值開始，降到最低值。

　　黃點是我們測量信號的時刻。已經確定了3個周期信號（0Hz， 1Hz， 2Hz），每個點為信號值的1/3.在這個例子里，周期［0 1 1］生成了時間量［2 -1 -1］，從最大值（2）開始，然后降到最低（-1）。

　　哦！剛才忘了考慮相位角了，現在我們要把它加上！加上數值：相位角。［0 1:45］是從45度開始的，1Hz的周期函數：

　　它是［0 1］的進階版本。時域上，我們用［.7 -.7］替換［1 -1］。因為我們的周期函數并不是沿著我們的測量時方向上，它們是還在運動的點（這是可被設置的）。

　　通過改變周期信號的頻率，強度和相位，傅立葉變換可以匹配任何時域信號。

　　信號所謂“時域觀測”或是“頻域成分”已成為一種抽象的概念。

　　說夠了，就讓我們把它講明白吧！你可以選擇模擬器里任何時間或類型的周期函數。如果它是時間表示的，你看到的許多構成所要周期函數的點（其集合被稱為波）。

　　

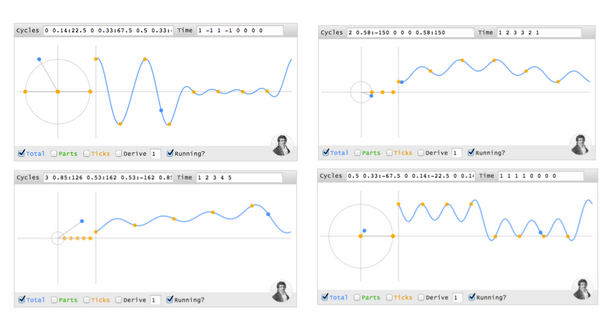
　　但是——難道在黃色的時間間隔里不包括任何特殊的點么？當然包括。但是我們怎么知道沒有測量的時候，信號是按照直線，曲線還是折線穿入另一象限呢？它在我們所需的等間隔時刻出現在我們希望的位置。

　　創造一個脈沖信號

　　我們可以用周期函數制造出一個脈沖信號么，像是（4 0 0 0）？（用括號表示時間點）

　　盡管脈沖看起來很煩人（難道只是煩人？），還是要考慮周期函數的復雜性。我們的周期成分必須對齊（最大值為4），然后向外傳播，每個周期函數都有其它函數可與其抵消。每個顯示為0的點，都是因為多個周期函數在此獲得平衡（你并不能關掉某個函數）。

　　讓我們看看每個時間點：

　　在0時刻，每個周期函數都處于最大值，（4？？？）由4個周期函數（0Hz 1Hz 2Hz 3Hz）疊加而成，每個函數的幅值都是1，而相位角都為0（換言之， 1 + 1 + 1 + 1 = 4）。

　　在之后的時刻（t = 1， 2， 3），所有周期函數的幅值必須相互抵消。

　　下面是數值為0的秘訣：當周期函數的值處于對稱軸的兩端（南和北，東和西，等等。），它們的和為0（要是3個周期函數均勻的分布在0，120和240度，它們就能相互抵消）。

　　想象許多繞圈旋轉的點。先面試每個點在每個時刻的位置：

　　時刻 0 1 2 3

　　------------

　　0Hz:0 0 0 0

　　1Hz:0 1 2 3

　　2Hz:0 2 0 2

　　3Hz:0 3 2 1

　　要注意，3Hz的周期信號從0開始，然后到了3，然后到了6（只有4個位置，6Mod，然后是9（9Mod4=1）。

　　每個周期長度為4個單位，周期函數在2個單位時的位置既不在一條線上（不同于0， 4， 8…），也不再相反的位置（不同于2， 6， 10…）。

　　好了。讓我們看看每個時間點的情況：

　　時刻 0：所有的周期函數都處于最大值（其和為4）

　　時刻 1：1Hz和3Hz函數值相互抵消（位置1和3是相反的值），0Hz和2Hz函數值相互抵消。最后結果為0.

　　時刻 2：在0時刻，1Hz和3Hz函數值相等，在2時刻，0Hz和2Hz函數值相等（相反的值）。相加結果還是0.

　　時刻 3：0Hz和2Hz函數值相互抵消.1Hz和3Hz函數值相互抵消。

　　時刻4（重復時刻0的情況）：所有函數值相等。

　　秘訣在于讓相互獨立的函數相互抵消（0Hz 和 2Hz， 1Hz 和 3Hz），或是讓同方向上數值和相互抵消（0Hz + 2Hz 和 1Hz + 3Hz）。

　　當每個周期屬性相等，相位為0時，就可以對齊并消去后面的值。（我并不能很好的證明這一點——有人能嗎？——但你可以自己看到其發生。試試［1 1］， ［1 1 1］， ［1 1 1 1］，你會注意到一個脈沖波峰：（2 0）， （3 0 0）， （4 0 0 0））。

　　這里直觀的顯示了怎么對齊，接下來是消去相反值：

　　

　　改變峰值時間

　　t=0時，什么都沒有發生。接下來換到（0 4 0 0）？

　　應該和（4 0 0 0）看起來差不多，但是周期函數必須在t=1時（當前時刻的1s后）對齊。然后要考慮相位。

　　想象有4個人參與的賽跑。賽跑開始時，4個人都在起跑線上，（4 0 0 0）。沒意思。

　　怎么能讓每個人都同時到達終點呢？很簡單。只要讓他們不停的你追我趕就行了。也許奶奶在終點線前兩英尺，Usain Bolt離線還有100米，他們可以拉著手一起穿過終點線。

　　相位變化，起始角度就是周期信號世界里的延遲。接下來要說怎么調整起始位置，來者每個周期都延遲1秒：

　　0Hz周期函數不發生移動，所以它已經對齊了

　　1Hz函數在4秒完成一次往復，所有延時一秒意味著1/4輪。相位延遲90度（-90），然后它在t=1時刻到達相位0，其最大值。

　　2Hz函數的變化速度是1Hz函數的兩倍，所以要兩倍的角度來滿足要求（-180或180，分別沿著不同的方向）。

　　3Hz函數的速度是1Hz函數的3倍，所以要有3倍的移動距離（-270或90度的相位改變）

　　如果時間點（4 0 0 0）是由函數［1 1 1 1］產生，那么（0 4 0 0）則是由［1 1：-90 1:180 1:90］產生。（ 注意： 此處用1Hz來表示一個周期運動經過的時間）。

　　天吶——我們在腦子里算出了周期函數！

　　干擾可視化是與之類似的，除了要在t=1時刻進行對齊。

　　

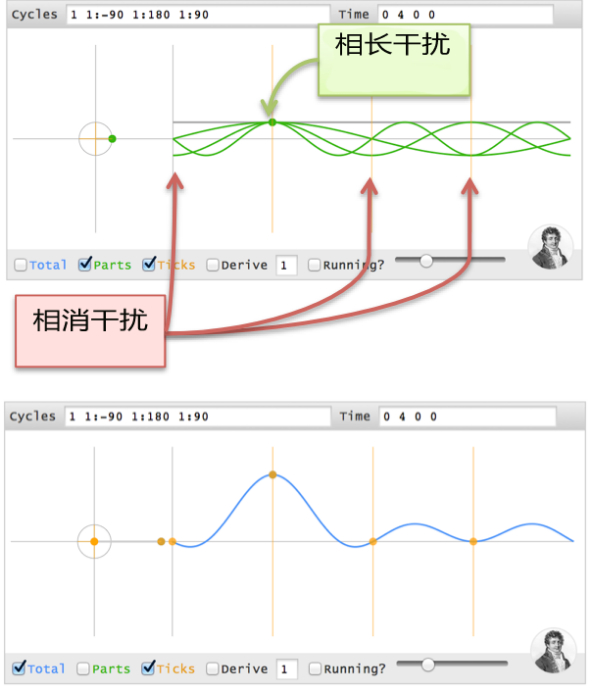
　　試一下這個：你能想象出（0 0 4 0），即2秒延時時候的情況么？0Hz沒有相位。1Hz是180度，2Hz是360度（也就是0度），3Hz是540度（即180度），結果為［1 1:180 1 1:180］。

　　完整的傅立葉變換

　　事實上：我們的信號只不過是一大堆脈沖信號的疊加！只要得到每個時刻組分，你就能知道整個信號的成分。

　　傅立葉變換通過頻率得到“配方”：

　　把連續的信號（a b c d）分成不同的時刻：（a 0 0 0） （0 b 0 0） （0 0 c 0） （0 0 0 d）

　　任意頻率（例如2Hz），試驗配方是“a/4 + b/4 + c/4 + d/4“（每個尖峰的強度被除以頻率數目）

　　等等！還要對每個脈沖設置延時（每一秒延時的角度取決于頻率）。

　　每個頻率真正的配方=a/4 （無延時） + b/4 （1秒延時） + c/4 （2秒延時） + d/4 （3秒延時）。

　　遍歷每個頻率就能得到完整的變換結果。

　　這就是從“數學文字”到真正數學的過程：

　　

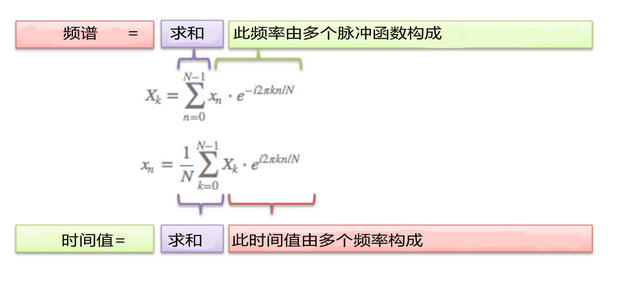
　　幾個要點：

　　N=時間樣本的數量

　　n=當前運算的樣本編號（0 。。 N-1）

　　xn=n時刻信號值

　　k=當前頻率（0Hz到N-1Hz）

　　Xk=信號中頻率k的值（幅度和相位，一個復數）

　　1/N被用于反變換（從時域信號轉化為頻域信號）。這是可以實現的，盡管我更喜歡用1/N進行正變換，它表示了脈沖信號的正真大小。你也在變換過程（正反變換中仍含有1/N）中使用1/sqrt（N）。

　　n/N是我們經過的時間比例。2πk是單位為弧度/秒的速度，e^-ix是反向經過的路徑。合起來就是以當前時間和速度經過的實際路程。

　　傅立葉變換的原始方程只告訴你“加上復數”。很多變成語言并不支持直接使用復數，因此要把它們轉化成直角坐標系，然后相加。

　　讓我們開始吧

　　這是我遇到的最有挑戰性的課題。傅立葉變換涵蓋了幾個要點（離散/連續/有限長/無限長）的高深數學（狄拉克δ函數），很容易遺漏掉一些細節。這真的很挑戰我的認知。

　　但仍有簡單的類比來說明這些——我拒絕用別的方式思考。無論是思暮雪還是Usain Bolt & Granny穿過終點線，都能讓我們輕易的理解這一點。這個比喻是有缺陷的，但不算壞：它是一個木筏使用，一旦我們過河就把它們留下。

　　我意識到我自己的理解是如何薄弱，我沒辦法在自己的腦海里想出（1 0 0 0 ）的變換。對我來說，就像，我懂加法。但是，“1+1+1+1”到底等于幾呢？為什么不呢？難道這些最簡單的運算不該有個直觀的展示么？