《線性及開關電源的控制環路設計》是Power Electronics前專欄作者Christophe Basso的最新著作。此著作注重探討工程師真正需要了解的補償及穩定給定控制系統的知識。本文包含此書有關穩定性標準章節的摘錄內容。

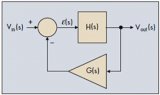
　　在電子領域，振蕩器是一種能夠產生自激正弦信號的電路。在多種多樣的配置中，振蕩器的加速過程牽涉到采用振蕩器的電子電路固有的噪聲。上電時噪聲等級上升，此時開始振蕩及自激。此類電路可采用圖1所示的構成模塊組成。如您所視，此配置看上去非常接近于我們控制系統的配置。

　　圖1：振蕩器實質上是一種誤差信號，不會妨礙輸出信號變化的控制系統。

　　在我們的示例中，勵磁輸入并非噪聲，而是電壓電平Vin，它被注入為輸入變量以啟動振蕩器。直接通道由傳遞函數H（s）構成，而返回通道包含G（s）區塊。要分析此系統，我們首先通過輸出電壓與輸入變量的變化關系方程式來寫出其傳遞函數：

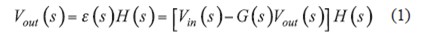
　　如果我們擴充此公式及Vout（s）項，我們就得到

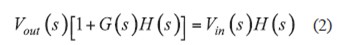
　　故此類系統的傳遞函數就是：

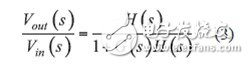
　　在此方程式中，乘積G（s）H（s）稱作環路增益，其標記為T（s）。要將我們的系統轉換為自激振蕩器，則必須存在輸出信號，即使輸入信號已消失。為了滿足這樣的目標，就必須符合下列條件：

　　要在Vin消失條件下驗證此方程式，商數（quotient）就必須無限大。商數無限大的條件就是特征方程式D（s）等于0：

　　要滿足此條件，G（s）H（s）必須等于-1。換句話說，環路增益的大小就必須為1，其符號應當改為負號。正弦信號的符號改變只不過是相位翻轉180°。這兩個條件能以下面兩個方程式來進行數學表述：

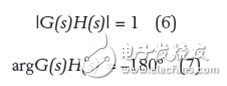
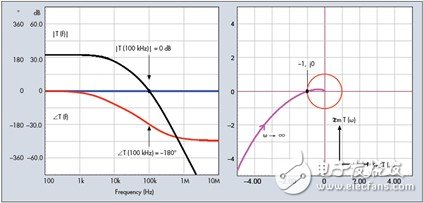
　　圖2：振蕩條件能以波特圖或奈奎斯特圖來表述。

　　在滿足這兩個方程式的條件下，我們就得到穩態振蕩條件。這就是所謂的巴考森（Barkhausen）標準，由德國物理學家Barkhause在1921年提出。實際上講，在一個控制環路系統中，它表示修正信號不再抗拒輸出，而是相位形式返回，振幅恰好與勵磁信號相同。方程式（6）和（7） 在波特圖（Bode plot）中表示環路增益曲線，此曲線穿過0 dB軸，且恰好在此點受180°相位滯后影響。在奈奎斯特分析中，環路增益的虛數及實數部份相對頻率的變化關系被繪制成圖，此點對應于-1， j0。圖2顯示了滿足振蕩條件的兩個曲線。如果系統略微偏離這些值（如溫度漂移、增益變化），輸出振蕩要么會以指數形式下降至0，要么振幅發散，直到達到較高或較低的電源軌。在振蕩器中，設計人員竭力盡可能多地降低增益余量，使振蕩條件在多種工作條件下都能滿足。

　　穩定條件

　　如您所知，控制系統的目標不是構建振蕩器。我們希望控制系統提供高速、精確及無振蕩的響應。因此，我們必須避開滿足振蕩或發散條件的配置。一種方式是限制系統會作出反應的頻率范圍。就定義而言，頻率范圍或帶寬，對應于從輸入到輸出之閉合環路傳輸通道下降3 dB的頻率。閉合環路系統的帶寬能被視作頻率范圍，在此范圍內系統被認為會極佳地響應其輸入（即遵循設定點或有效地抑制擾動）。我們在后文會看到，在設計階段，我們并不直接控制閉合環路帶寬，但會控制交越頻率（crossover frequency） fc——這是一項跟開環路分析有關的參數。這兩個變量通常被概略認為相等，但我們會看到這僅在一種條件下成立。然而，它們相差得也不太遠，在討論中這兩項能互換。

　　我們已經看到，開環路增益是我們系統中的一項重要參數。當增益存在時（即|T（s）|》1），系統以動態閉合環路工作，能補償輸入的擾動或對設定點變化作出反應。然而，系統反應也存在限制：系統必須在擾動信號所涉及的頻率提供增益。如果設定點變化的擾動太快，勵磁信號的頻率成分就低于系統帶寬，表示這些頻率缺少增益：系統變慢且不會作出反應，工作狀態就像環路對波形變化沒有響應。那么，是否就要求無限大的帶寬呢？不是的，因為增加帶寬就象是拓寬漏斗的直徑：您當然可以收集到更多信息，并對輸入振動更快地作出反應，但系統也將接收到偽信號（spurious signal），如轉換器在某些情況下自己產生的噪聲及寄生參數（如開關電源中的輸出漣波）。因此，強制要求將帶寬限制在您應用真正要求的范圍。采用的帶寬太寬將削弱系統的抗噪聲性能（如其抑制外部寄生信號的強固性）。

　　限制帶寬

　　我們怎樣限制控制系統的帶寬？方法就是通過補償器區塊G改變環路增益曲線。此區塊將確保在一定量的頻率fc后，環路增益的大小|T（fc）|下降至低于1或0 dB。如同我們所闡述的，一旦環路閉合，它大致就是您的控制系統的帶寬。發生此現象時的頻率稱作交越頻率，標作fc。這就是否足夠獲得強健的系統？不是的，我們需要確保另一個重要參數：幅值為1的點的相位T（s）必須低于-180°。從我們的實驗來看，我們已經看到當環路增益在交越頻率處低于-180°時，我們獲得了朝穩態收斂的響應。這很明顯是我們控制系統極想要的一種特征。為了確保我們在交越時避開-180°，補償器G（s）必須在選定的交越頻率處訂制環路幅角（argument）以構建相位余量（phase margin， PM或φm）。相位余量可以被視作一項設計或安全限制，確保在即使存在外部擾動或不可避免的生產差異范圍（production spread）的情況下，環路增益的變化不會破壞穩定性。我們在后文會看到，相位余量還會影響系統的瞬時響應。因此，相位余量的選擇并不只是取決于穩定性考慮因素，還取決于您期望的瞬時響應類型。相位余量的數學定義如下所示：

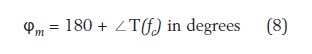
　　其中T代表開環路增益，其中包括分級的控體H和補償器G增益。

　　圖3中顯示了經典補償的典型環路增益曲線，其中顯示交越頻率為6.5 kHz。在此點，T（s）相位為-90°。如果您想在6.5 kHz時從-180°起步，并正向清點相位度數直至穿越幅角波形，您在此例中就得到90°的相位余量。這就是一個極為強健的系統，被認為在各種條件下都穩定：即使在交越點附近環路增益有一定程度的變化，也沒有可能在相位余量太小的頻率交越。所謂的“太小”，我們指的是相位余量接近30°極限，低于此值時系統就提供不可接受的振鈴（ringing）響應。這就是為什么您在上學時學習到45°是極限，此值相較于30°而言提供了額外的余量。我們稍后會看到這些數字的來源分析。

　　圖3. 在此示例中，0 dB交越點位于6.5 kHz，此頻率時總相位滯后提供了90°的相位余量

　　增益余量及穩定條件

　　圖4顯示了被補償轉換器的另一個典型頻率響應，重點顯示了0 dB交越點及相位余量。我們根據經驗可知，構成轉換器的元件在產生生命周期內會再現性能變化。這些變化可能是因正常的生產差異范圍引起的（如電阻或電容遭受逐批次公差不同的影響）。轉換器的環境工作條件也對元件有影響。在這些變量中，溫度充當關鍵角色，影響被動或主動元件參數，如電容或電感等效串列電阻（ESR）、光耦電流傳遞比（CTR）或是雙極晶體管的beta值。這些變量影響環路增益，使其上升或下降，具體則取決于受影響的參數。

　　圖4. 環路增益會顯示出對溫度等外部參數的敏感性。出現變化時，相位余量必須始終保持在安全限制范圍內。

　　如果增益曲線出現變化，0 dB交越頻率將過渡至新的值，為轉換器施加不同的帶寬。在這些變化條件下轉換器的穩定性會受到怎樣的影響？如果新的交越頻率出現在相位余量較少的點，瞬時響應性能可能下降，使過沖不再能被接受。因此，身為設計人員，你的責任就是確保這些差量（dispersion）在你接近-180°極限時不會突然增大增益。您需要充足的增益余量，其定義如下所示：

　　它對應于恰好為-180°或弧度的頻率點（圖3中為1 MHz）。

　　圖4描繪了由于所選擇元件生產差異范圍導致的±10 dB典型增益變化。它帶來了1.5 kHz至30 kHz的交越頻率。在此區域，相位余量從70°變為45°，這些都是理論上的安全數字。最壞情況是什么？就是新的交越頻率在總相位滯后180°處出現。這條件在1 MHz時出來，表示有35 dB的正增益變化。

　　不太可能有大增益

　　有利的是，當今電子電路中不太可能出現35 dB的增益變化。以前，在變壓器或伺服系統（servomechanism）采用真空管電路驅動的時候，上電序列期間的準備（warm-up）時間可能引起大的環路增益變化。因此，增益規定有必要排斥可能存在穩定性風險的第二個點。此總相位滯后達-180°的頻率處的環路增益曲線上可見這增益余量，在圖3中被標記為GM。在當今電子電路中，高于10 dB的增益余量通常就足夠了，除非您的環路增益對外部參數極為敏感。

　　增益漂移的另一個示例如圖5所示。圖中顯示另一個被補償的轉換器在10 kHz時出現80°的相位余量。根據前文的討論，我們知道可能會出現增益變化，致使增益曲線上揚或下走。在我們的示例中，我們可以發現2 kHz附近一個區域的相位余量小到只有18°。如果出現20至25 dB的增益下降，你最后得到的控制系統就會出現相當危險的約2 kHz的低相位余量。這就會導致振蕩響應，很可能超出過沖規范。此類系統被認為是有條件穩定。有利的是，如前所述，25 dB的增益變化并不常見，有這等增益余量的系統可被視為強健。然而，我看見過在一些設計案例中，最終使用者（您的客戶）在規范中清晰標明不接受有條件的設計，要求在低于交越頻率的所有點提供大于60°的相位余量。在這種情況下，就強制要求補償轉換器，使得無論什么工作條件下，低于交越頻率時都不存在相位余量降低的區域。

　　圖5. 在此示例中，如果增益漂移至低于25 dB，曲線就在相位余量僅為18°的頻率點過0 dB軸。如此的相位余量將受大的過問影響，提供振蕩極大的響應。這就是有條件穩定的案例。

　　穩定，或是不穩定？

　　通常認為，在交越前相位下降至低于-180°的系統是不穩定的系統。這樣的響應如圖6所示。在1 kHz后相位曲線快速下降，并在1.5 kHz之后的數kHz范圍內越過-180°的極限。然后相位曲線又上揚，在10 kHz時提供50°的相位余量。是的，此系統很穩定，只不過是因為在0 dB時我們不滿足方程式（7）。要記住的是，要消除方程式（3）的分母，您必須使增益大小恰好等于1且相位滯后180°或更多。在圖中，我們可以看到任何點都不滿足此條件。然而，值得一提的是，此環路極具條件相關性。如果增益減少數dB，您的相位余量將變得低于45°。增益再下降10 dB，您將進入相位余量為0的危險區，這時會達到振蕩條件。

　　圖6. 相位滯後180°，但處於增益大於的區域。這並不構成問題，其回應可以接受。

　　注：本文經出版商Artech House， Inc.， Boston批準，節選自《線性及開關電源控制環路設計教程》（c） 2012一書。此書的主題包括：環路控制基礎、傳遞函數、控制系統的穩定條件、補償、以運算放大器為基礎的補償、以運算跨導放大器為基礎的補償、以TL431為基礎的補償、以為流穩壓器為基礎的補償 、測量及設計實例。此書可以ArtechHouse.com、Amazon.com或BN.com上購買。