工程問題本質上是解決兩個“流”的問題，一個是“信息流”，另一個是“動力流”。我們前面說到的自動控制，信號處理其實都屬于“信息流”的范疇，解決的是大腦和神經(jīng)的問題，而“動力流”，則是要解決肌肉問題。只有兩個“流”處理好了，才能做出一個成功的工程。今天，我們就來說一說“動力流”的核心部件之一——電機。

電機（Electrical Machine）本質是一個能量轉換裝置（電能和機械能互換），包括電動機和發(fā)電機。工業(yè)中電動機更常見一些，因此狹義的電機通常是指電動機。

那磁鐵和永磁電機有什么關系呢？——永磁電機就是利用磁鐵制作的電機，只不過磁鐵這個名字不夠高大上，專業(yè)術語一般叫“永磁體”。電現(xiàn)象和磁現(xiàn)象人類早就已經(jīng)了解，但是直到19世紀，電學和磁學的研究仍處于很基礎的階段，而且絕大多數(shù)物理學家都認為電和磁是兩種完全不同的現(xiàn)象。第一次工業(yè)革命后期，電磁學才逐漸合體并開始蓬勃發(fā)展起來，并催生了第二次工業(yè)革命——電力革命，這其中貢獻最大的有這么幾個人：奧斯特、安培以、法拉第以及高斯等，他們最重要的的工作都完成于1820年至1831年，最后由開了掛的麥克斯韋進行了總結并提出了完整的電磁理論。電機的基本理論和工程實現(xiàn)基本都是在這一時期成型的，因此要想學習電機，了解基本的電磁理論發(fā)展過程是非常有必要的。

一、電和磁到底有沒有關系？——奧斯特：電流的磁效應

19世紀以前，人們一直以為電與磁勢完全不同的現(xiàn)象，沒有什么聯(lián)系，雖然有一些零星的物理現(xiàn)象暗示它們之間似乎有一些說不清道不明的關系。直到1820年7月，丹麥的物理學家奧斯特（H.C.Oersted，1777-1851）發(fā)表了一篇文章《關于磁針上電流碰撞的實驗》，向科學界宣布了電流的磁效應——電和磁其實是一對CP。

奧斯特的論文起源于一個很偶然的實驗——在電池的兩極之間接上一根很細的鉑絲，在鉑絲的下方放置一枚磁針，然后接通電源，很正常的操作，貌似沒什么，但是現(xiàn)象卻很令人吃驚——小磁針轉動了，一直轉到鉑絲垂直的方向，改變電流方向，又發(fā)現(xiàn)小磁針向相反方向偏轉。

奧斯特的發(fā)現(xiàn)揭示了長期以來認為性質不同的電現(xiàn)象與磁現(xiàn)象之間的聯(lián)系，電磁學立即進入了一個嶄新的發(fā)展時期，法拉第后來評價這一發(fā)現(xiàn)時說：“它猛然打開了一個科學領域的大門，那里過去是一片漆黑，如今充滿光明。”人們?yōu)榱思o念這位博學多才的科學家，從1934年起用“奧斯特”的名字命名磁場強度的單位。

奧斯特可能怎么也沒有料到，從1820年7月發(fā)表電流的磁效應的文章后，僅僅經(jīng)歷了四個多月時間，電磁學就經(jīng)歷了從現(xiàn)象的總結到理論的歸納一次大飛躍，從而開創(chuàng)了電動力學的理論。而推動這一發(fā)展的，是一個我們非常熟悉的人——安培。

二、電如何產(chǎn)生磁？——安培定律

前面我們說到，能斯特發(fā)現(xiàn)了電流的磁效應，這個實驗結果強烈震撼到了安培——一個被稱之為“電學中牛頓”的大神。安德烈·瑪麗·安培（André-Marie Ampère，1775 — 1836）出生于法國里昂，是我們學物理學的最早認識的科學家之一，因為電流的單位就是“安培”。

200年前的科學界和現(xiàn)在也差不多，那就是一個熱點文章發(fā)表后，總有一大群人蜂擁上來，發(fā)表灌水文章。安培在看到奧斯特的電流的磁效應的文章后，也立馬開始了這一熱點領域的研究。顯然安培不屬于灌水的這一類人，因為他不差名氣和聲望，驅使他前進的，是他對自然規(guī)律的好奇心。

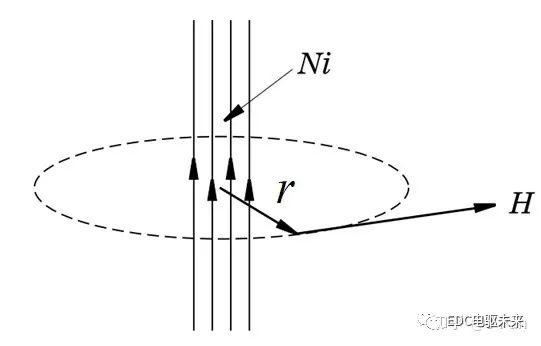
安培通做電流做實驗，發(fā)現(xiàn)長直導線外，到導線距離相等的點，“磁場”大小相同；距離不同的點，“磁場”大小隨著距離成反比；“磁場”和電流大小以及導線的根數(shù)也成正比。我們不妨用 字母??來表示“磁場”的大小，則很容易得到：

或者更任性一點，我們可以定義沿半徑為??的圓上，其“磁場”大小為：

當然，安培是不會滿足于到此為止的，因為這實在算不上的什么重大發(fā)現(xiàn)——那不是圓怎么辦，如果是任意曲線呢？——安培偉大的地方在于，他還真的將“圓”擴展到了任意曲線上。

安培定律完整的表述為：在恒定電流的磁場中，磁場強度??沿任何閉合路徑??（即環(huán)路積分）的線積分等于其所包圍的電流強度的代數(shù)和，寫成數(shù)學的樣子就是：

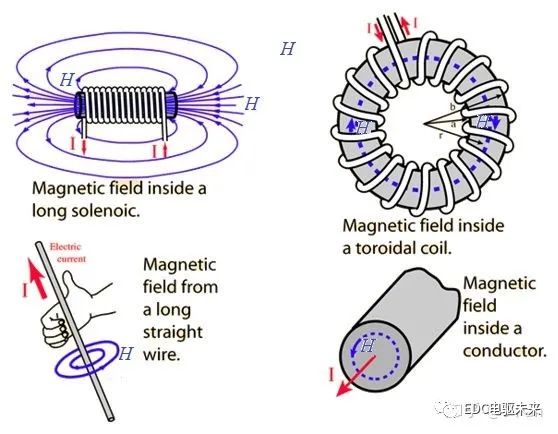
這個公式暗含一個結論，那就是磁場是由運動的電荷（即電流）產(chǎn)生的，安培認識到磁現(xiàn)象的本質是電流 ，把涉及電流、磁體的各種相互作用歸結為電流之間的相互作用，提出了尋找電流元相互作用規(guī)律的基本問題。因此在電磁學中，把產(chǎn)生磁場的電流也叫磁動勢或磁勢（Magnetomotive Force），簡寫為MMF，注意這是一個非常重要的概念，很多我們熟悉的磁場，都可以應用安培環(huán)路定理來計算。

三、磁如何產(chǎn)生電？——法拉第電磁感應定律

法拉第（Michael Faraday，1791-1867），英國的物理學家。法拉第可以說是實驗物理學家的代表，一生做了無數(shù)次的實驗，遍布整個電磁學領域，其中最具代表性的，就是電磁感應定律了：磁通量變化產(chǎn)生感應電動勢。

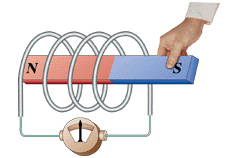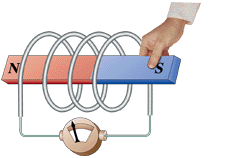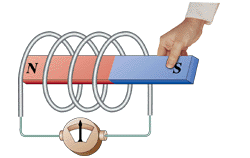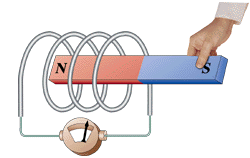
電磁感應定律的定量描述為：線圈中感應的電動勢（Electromotive Force），簡稱EMF，與每匝線圈中磁通量的變化率以及匝數(shù)成正比，寫成公式就是：

那么，問題就來了——什么是磁通量？其基本定義是：

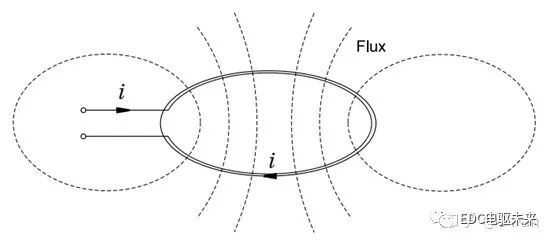
簡單來說就是磁通密度乘以面積，面積好理解，那磁通密度是什么？——與電場強度??是由單位點電荷受電場力類似，磁通密度可以根據(jù)運動電荷在磁場中所受到的磁場力來定義。實驗發(fā)現(xiàn)：一個電荷??以速度??在均勻磁場中運動，會受到電磁力??，這個力和磁場的強弱是成正比的，即：

這個公式是洛倫茲公式的簡化版，也就說，我們可以通過電荷大小、運動速度以及所受到的力來反推周圍磁場的大小，這個磁場的大小就是磁通密度，也叫磁感應強度，單位是特斯拉（Tesla）。注意，磁通密度是電機中最重要的概念之一。

四、什么是B-H曲線

細心的童鞋會發(fā)現(xiàn)一些端倪：

在介紹安培環(huán)路定理的時候，我們說電流可以產(chǎn)生磁場，磁場的大小可以用??來表示：

在介紹法拉第電磁感應定律的時候，我們又說可以通過受力，來計算電荷感受到的磁場??。

都是磁場，為啥用兩個量表示？他們是一回事嗎？——首先，可以明確一點，這倆貨量綱都不一致，肯定不是一回事。

我們一般把磁場密度??與磁場強度??之間的比值稱之為磁導率：

磁導率描述的是電荷感受的磁場（輸出）與電流產(chǎn)生的磁場（輸入）的比值，描述前者隨著后者的響應。既然是響應，就會有幅值響應和相位響應，所以本質上，磁導率是一個復數(shù)，只不過呢，在電機里面都是工作在低頻段，相位滯后很小，可以忽略，一般只看幅值關系。

為什么介質中磁場輸入和輸出不一樣呢？——因為介質有了響應。我們現(xiàn)在設想通過電流??，把磁場??加到某種材料當中，材料中的帶電粒子受到磁場的響應，進而產(chǎn)生了一些附加磁場，在該點處的總磁場不再是??了。受外界磁場影響使得材料里也有內(nèi)部額外磁場的過程，叫做“磁化”。

Source: Dr. Cox

簡而言之，??是外部的激發(fā)場，??是總的響應場，在電機里面，這兩個量都非常重要，因為電機就是要考察電壓、電流以及力矩之間的關系，而：

電流和??相關；

力矩和??相關；

因此，理解??和??的關系，是學習電機的一個非常必要的知識點。

現(xiàn)在假設我們用一個正弦的電流對介質進行磁化，電流（代表??）變化如左下圖，得到介質中總的磁場（??）為右下圖：

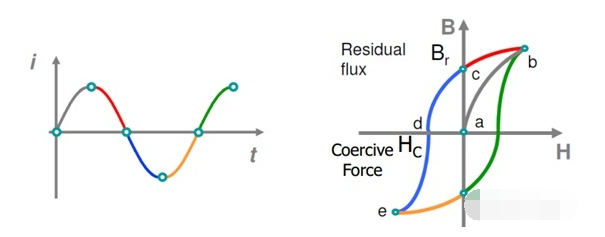
Source:Dr. Cox

其中，??表示剩余磁通密度（Remanent Flux Density），簡稱剩磁；??表示矯頑力（Coercive Force），可見??和??并不是一個簡單的線性關系，呈現(xiàn)出一個滯環(huán)，一般稱之為磁滯曲線。

不同的材料代表不同的介質，其磁滯回線也不一樣，如下圖所示：

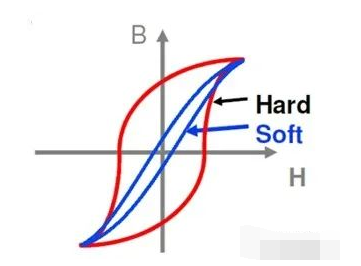
Source: Dr. Cox

有的材料滯環(huán)較寬，也就是當勵磁電流減為零后，總的磁場??仍保持在一個較大的值，我們稱之為硬磁材料或永磁體。

有的材料滯環(huán)較窄，也就是當勵磁電流減為零后，總的磁場??也基本減小到零，我們稱之為軟磁材料或導磁體。

五、什么是永磁同步電機

1821年，法拉第制作了一個裝置，這個裝置能將電能轉化成機械能，被認為是世界上第一臺電動機。

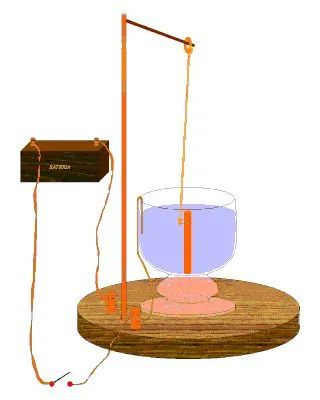
法拉第的裝置的組成非常簡單：將水銀注入一個圓形容器里面，中間放置一塊永磁體，一根長的導線一端懸掛，另一端浸入容器里的水銀里面，最后再外接一個直流電源。原理也很簡單，永磁體產(chǎn)生的磁場與導線產(chǎn)生的磁場相互作用，產(chǎn)生一個使導線繞軸旋轉的力。法拉第的天才之處在于想到了用水銀（常溫液體，有良好的導電性）解決了電機連續(xù)旋轉的所需要的換向問題。

法拉第的電機驗證了機電能量轉換可以連續(xù)進行的，為電機的發(fā)展奠定了堅實的基礎。當然現(xiàn)代電機和法拉第的電機模型有了較大的區(qū)別，但原理都是完全一致的：都是兩個磁場相互作用。

5.1 電機原理的通俗理解

我們從小學就知道，磁鐵分N極和S極，磁力線從N極出發(fā)，最后回到S極；磁鐵同極相斥，異極相吸。磁鐵磁極之間的相互作用示意圖如下：

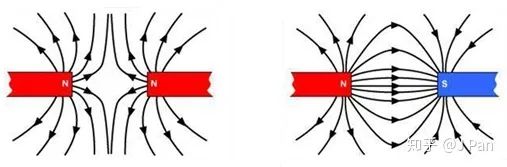
利用磁極之間的相互作用力，理論上我們可以移動一個磁極，讓另外一個磁極跟著運動，如果第一個磁極旋轉的話，另一個磁極也會跟著旋轉。但是這樣無法稱之為電機，因為旋轉一個磁極需要的是機械能，這樣本質上是機械能之間的轉換，不是電能和機械能之間的轉換。那怎么辦呢？

安培定律告訴我們，磁場本質是由電流產(chǎn)生的，我們想要的是磁場之間的相互作用，因此主要有電流即可，一個很自然的想法就是：能不能將兩個磁場中的一個用線圈來產(chǎn)生呢？——當然可以，永磁同步電機就是這么干的，具體見下圖：

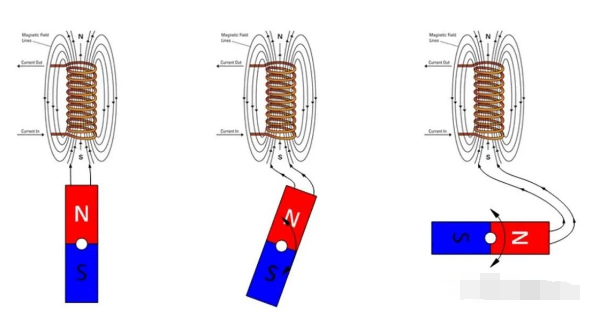
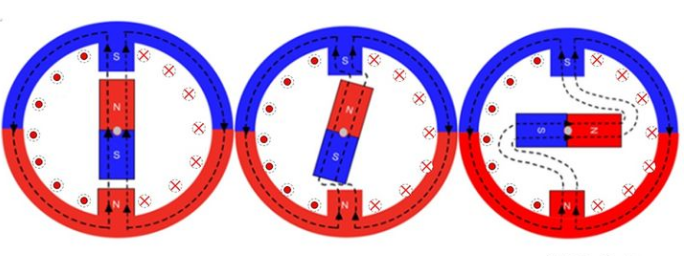
我們一般將永磁體放在轉子上，定子是一個線圈，線圈通電后，也會產(chǎn)生一個磁場。根據(jù)我們的直觀感覺，很容易得出如下結論：

當兩個磁場軸線正對著的時候（上圖左），磁場之間有相互吸引力，這個力是徑向的，不會產(chǎn)生轉矩。

當兩個磁場軸線有一定夾角的時候（上圖中），磁場之間有相互吸引力，但是這個力既有徑向分量，也有切向分量，因此會產(chǎn)生一定的轉矩。

當兩個磁場軸線垂直的時候（上圖右），磁場之間有相互吸引力，但是這個力主要是切向分量，因此產(chǎn)生轉矩最大。

可以做出如下猜想：對于旋轉電機而言，由于其轉矩是由兩個磁場相互作用產(chǎn)生的，因此：

轉矩的大小應該和兩個磁場的大小是正相關的，磁場越強，轉矩應該越大；

轉矩的大小和兩個磁場之間的夾角是正相關的，夾角為零時轉矩為零，夾角90°時轉矩最大。

這些都是定性分析，對于工程師而言，我們需要的是定量的計算，那怎么算呢？

我們知道，數(shù)學中的叉乘運算??描述的是什么東西呢？——叉乘的結果和兩個量的幅值成正比，和夾角正相關，這怎么和磁場產(chǎn)生轉矩的那么相像，那是不是可以可以用叉乘來計算兩個磁場相互作用產(chǎn)生的轉矩呢？

磁場的本質是電流產(chǎn)生的，產(chǎn)生磁場的電流又叫磁動勢，假如我們膽子更大一點，是不是可以進一步猜想：

其中??表示線圈磁動勢，??表示永磁體磁動勢。

也就是說電機轉矩和線圈磁動勢與永磁體磁動勢的叉乘成正比。這么想是合理的，后面我們會有證明。

當然，真正的電機是不會直接拿線圈和永磁體直接相吸的，這樣效率太低，一般是將線圈繞在磁軛上，磁軛是軟磁體，起著導磁的作用，如下圖所示。

5.2 電機的數(shù)學模型

電機就是一個能量轉換裝置，將電能轉化成機械能，轉換路徑是電能??電磁能??機械能，要分析這個過程，其實就是解決三個方程的問題：

磁路分析——磁鏈方程

電路分析——電壓方程

機械分析——轉矩方程

下面我們就按照這個思路，看看如何分析一個永磁同步電機。

我們前面說了，電機產(chǎn)生轉矩就是兩個磁場相互作用，當個磁場都在連續(xù)旋轉時，就產(chǎn)生了一個固定的旋轉力矩。要產(chǎn)生旋轉的磁場，就要有“旋轉”的電流；要產(chǎn)生“旋轉”的電流，就要有“旋轉”的電壓；同時旋轉的磁場還會產(chǎn)生“旋轉”的磁鏈，其示意圖如下：

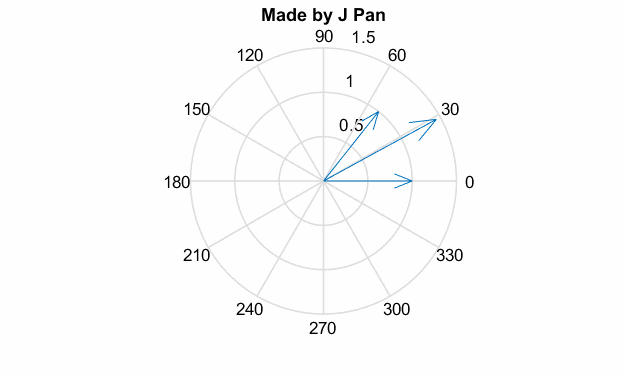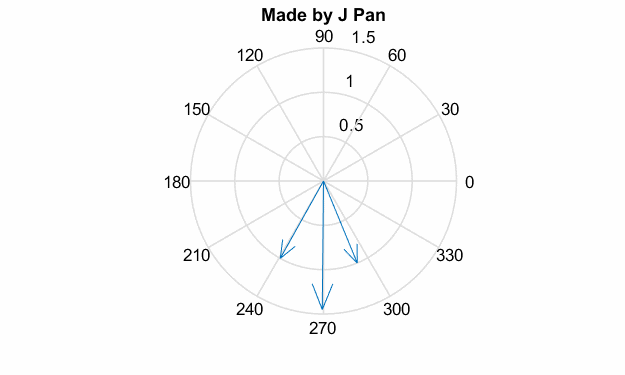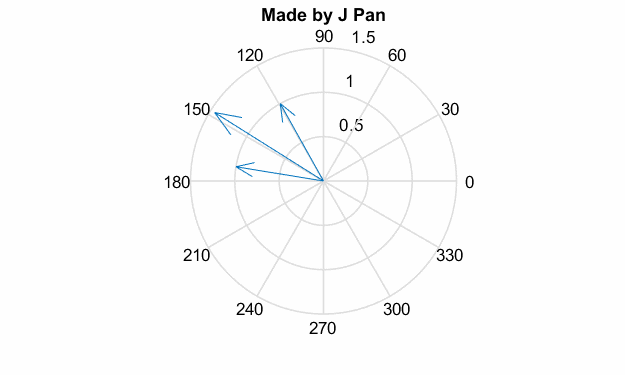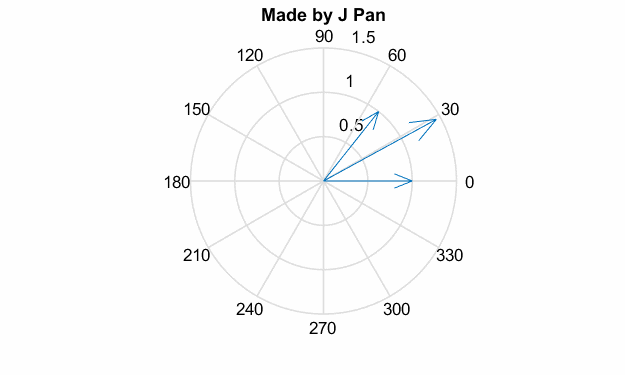
可以把電壓、電流以及磁鏈都看成是旋轉的矢量，其轉速完全一致，相位不同。數(shù)學表達如下：

電壓矢量：?

電流矢量：?

磁鏈矢量：?

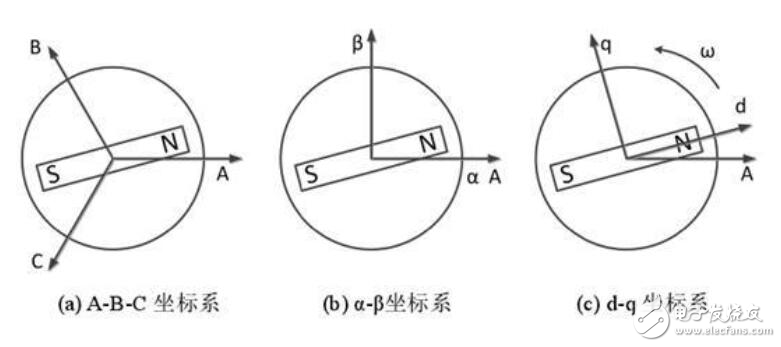
文章中，我們把旋轉的矢量用加粗帶箭頭的符號表示，把矢量用只帶箭頭的符號表示。電壓、電流以及磁鏈雖然以相同的速度在旋轉，但是其相位還是有差別的，因此，我們有必要定義一個基準，把這個相位信息表達出來。在電機里面，為體現(xiàn)逼格，我們一般不叫xy軸，而是把永磁體所在的軸線稱之為d軸（Direct Axis），也叫直軸，垂直于永磁體的軸線稱之為q軸（Quadrature Axis），也叫交軸。d軸和q軸相差90°電角度，示意圖如下：

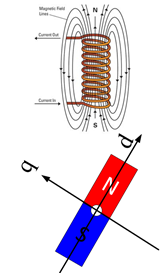
至于什么是電角度，我們后面會說。

5.2.1 磁鏈方程

磁鏈表征著磁場的信息，對于永磁電機而言，轉子一般是永磁體，所以只對定子線圈進行磁鏈計算即可。我們知道線圈磁鏈計算公式為：

?是通過單個線圈的磁通，??是線圈的總匝數(shù)。

電機中的磁場來源可以分成兩部分，一部分是線圈是產(chǎn)生的，另一部分是永磁體產(chǎn)生的。即：

其中??為線圈自身產(chǎn)生的磁鏈，??為永磁體產(chǎn)生的磁鏈。其向量圖如下圖所示。

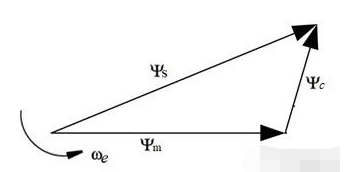
對于線圈而言，專門有一個量來表征線圈自身產(chǎn)生磁鏈的能力——電感，單位為亨利（H），

電感定義為：

即單位電流產(chǎn)生的磁鏈，電感和電阻類似，雖然是通過磁鏈和電流來定義和計算的，但是其本質是由磁路的物理結構決定的，與電流沒有關系（除非電流引起磁路飽和，相當于改變了磁路的物理結構）。

因此線圈產(chǎn)生的磁鏈可以表示為：

永磁體在線圈產(chǎn)生的磁鏈為：

5.2.2 電壓方程

電機中磁路主要研究磁鏈方程，而電路主要研究電壓平衡方程。忽略電機中的鐵損及漏磁等，對于定子線圈，模型可簡化成下圖所示：

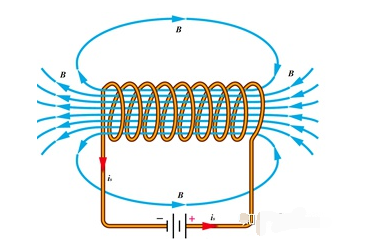
很容易得出：電路的外電壓等于電阻損失電壓與線圈感應電壓之和，寫成數(shù)學形式為：

將線圈的磁鏈分解成線圈電流產(chǎn)生磁鏈以及永磁體產(chǎn)生磁鏈：

其中：

假設磁路均勻，即電感是常值，令??，稱之為同步電抗，則：

永磁體產(chǎn)產(chǎn)生的感應電勢為：

此處也假設磁路均勻，則定子線圈總的感應電勢為：

不難發(fā)現(xiàn)：??存在是因為線圈中電流變化，導致了??變換而其引起的，其大小可用電感來表征，因此稱之為感生電勢或者是變壓器電勢；??存在是因為永磁體產(chǎn)生的旋轉磁場導致了線圈有效面積??發(fā)生改變而引起的，因此稱之為動生電勢或反電動勢。線圈中總的感應電勢即是感生電勢和動生電勢之和。

電壓平衡方程的矢量形式為：

畫成相量圖的形式為：

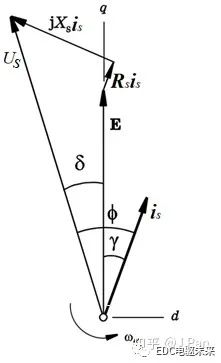
圖中??為動生電勢（反電動勢），??為感生電勢（電感電勢）。

注意：所有的相量都在旋轉。

我們前面定義了：

電壓矢量：?

電流矢量：?

磁鏈矢量：?

將上式代入電壓平衡方程可得：

對應的等效電路圖為：

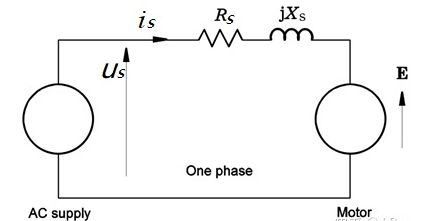
5.2.3 力矩方程

力矩是電機設計及控制中非常核心的一個量，一把書上要么是直接給出方程，要么是從能量轉換的角度推導出，要么太粗暴，要么太復雜，都不太容易理解，今天，我們從能量守恒的角度來看一下，希望能減輕一下各位童鞋的負擔。

電機，本質是一個能量轉換裝置，對于電動機來說，就是將電能轉換成機械能。在復平面域，計算出的功率稱之為復功率，與實數(shù)領域直接相乘略有不同，復平面對應的是電壓相量與電流相量的內(nèi)積：

代入電壓平衡方程可得：

根據(jù)內(nèi)積的定義??,這樣就可以得到電機進行能量轉換時的復功率：

方程的左邊就是流入電機的瞬時功率，這個比較好理解，我們著重分析一下方程右邊的兩項分別代表什么意思。

第一項：?

代表著電阻??在電流??下產(chǎn)生的功率，這個比較好理解，可以看成是熱損耗，電機中繞組由于大都是銅線繞指的，一般也叫銅損，最終損耗掉了。

第二項：?

，

由復數(shù)的計算規(guī)則：?

進一步化簡可得：?

我們知道，對于復功率而言，實部是有功功率，虛部是無功功率。取這一項的實部即為有功功率，所以：

這個式子看著有點嚇人，但是化簡一下就簡單明了了：

上式的右邊看著是不是有什么規(guī)律呢？——?

所以最終的有功功率非常簡單：?

式中??表示叉乘后的方向（含全面的符號），加上它是為了形式上一致，因為點乘后標量，叉乘后是矢量。

知道了有功功率，這個時候我們就很容易計算轉矩了，假定轉子的轉速是??,則轉子上的力矩為：

其中?為極對數(shù)，這一塊很多童鞋是由迷惑的，我們說?為電角度，??為機械角度，它倆到底有什么關系？什么時候用電角度？什么時候用機械角度？

我們前面舉例子時一般都是一對極，這樣沿機械一周，電信號也變化一個周期，此時機械角度與電角度相同，即??；當極對數(shù)??大于1時，這樣沿機械一周，電信號就會變化??個周期。下圖給出了3對極和6對極時每個機械周期內(nèi)（360°）電信號變化的情況。

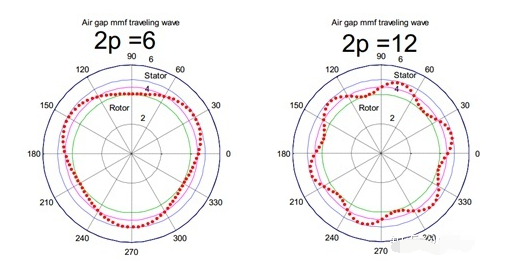
可見，??。

由于

所以力矩還可以寫成：

由于??，所以轉矩還可以寫成：

前面我們猜測：

在這里也可以得到證明，因為??，??。

5.3 DQ坐標系下三大方程

前面我們所有的三大方程（磁鏈、電壓、轉矩）都是用矢量來表示的，形式是相當簡潔的，但是考慮到大多人還是習慣標量的表示方法，而且矢量運算在計算機中也不容易實現(xiàn)，所以大多數(shù)教材上一般都是給出標量形式下的電機三大方程。

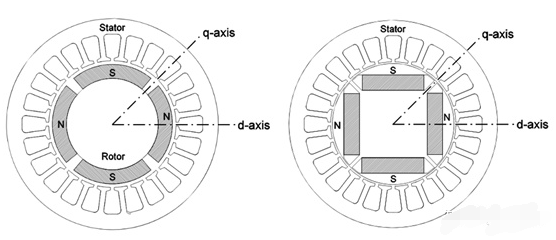
我們首先將電壓、電流及磁鏈矢量投影到dq坐標系上：

帶入到原始旋轉矢量方程：

代入電壓平衡方程可得：

化簡可得：

則通過簡單的數(shù)學運算，很容易得到??坐標下標量形式的磁鏈方程：

?坐標下標量形式的電壓方程：

畫成相量圖的形式如下：

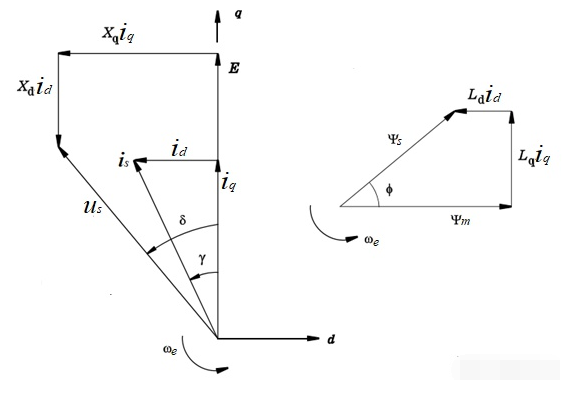
?坐標下矢量的力矩方程：

標量形式 力矩方程為：

進一步變形：

這就是教科書上最常見的形式了，這表明：永磁同步電機的力矩包含兩個部分，一是??，這是由永磁體產(chǎn)生的力矩，一般稱之為勵磁力矩或對齊力矩（Alignment Torque）；另一部分??是由于磁路上磁阻不均勻（??）引起的，所以稱之為磁阻力矩，如果磁路交直軸磁阻相等，則這部分力矩消失。

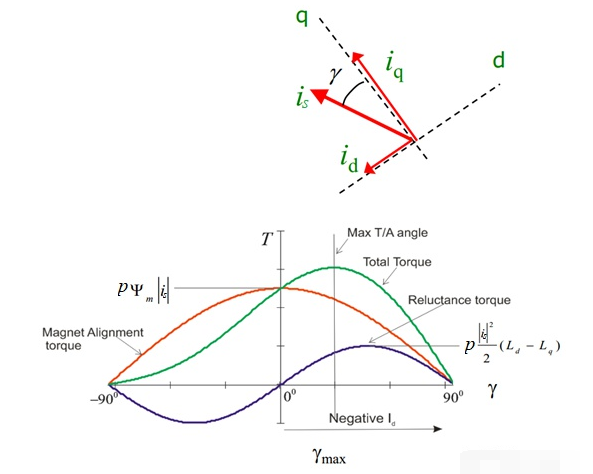
Source: Dr. Galea?

將??、??用電流幅值及角度進行表示，輸出轉矩為：

上式對??求導，并取導數(shù)為零，即可以得到轉矩取極值時對應的??值：

，其中?

上式中，位移的未知量是??，也就說有了測量到了電流值，就可以計算出??，從而獲得最大的轉矩——這就是最大轉矩比電流控制（Maximum Torque per Ampere），簡稱MTPA。

六、什么是電壓極限圓和電流極限(橢)圓

我們令：

前面我們介紹了??坐標下電壓方程為：

現(xiàn)在我們考慮穩(wěn)態(tài)時情況，先忽略電阻??（通常比較小），穩(wěn)態(tài)時??、??不再變化，因此電壓平衡方程可以簡化為：

為簡單起見，先假定??則：

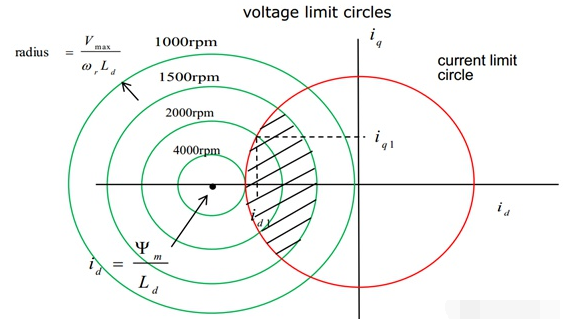
Source: Dr. Galea

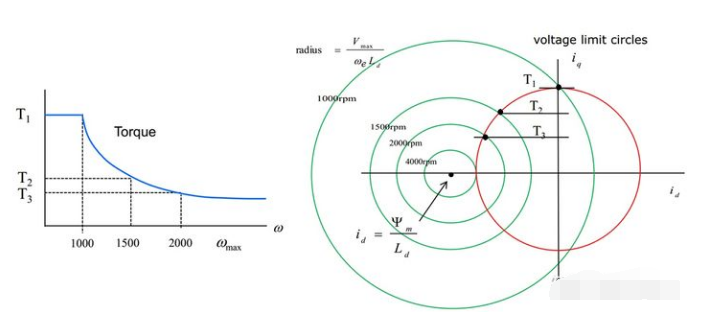
其中綠色為電壓極限圓，紅色為電流極限圓。電機的電壓是由逆變器提供的，是有限制的，也就是說??，很顯然能得出以下幾個結論：

電壓極限圓不是正好在電流坐標系的中心，偏置為??;

轉速越高，電壓圓的半徑越小；

電機必須工作在電壓圓與電流圓同時覆蓋的區(qū)域（截面線示意的部位）

當電機轉速很低時，電壓極限圓很大，電流極限是其主要約束，因此低速下電流可以一直保持在??為最大值狀態(tài)，此時稱之為恒轉矩區(qū)，如下圖所示的T1區(qū)。當轉速繼續(xù)上升時，電壓和電流極限圓都成為約束，兩者的交點處為工作點，如下圖的T2和T3區(qū)，??開始出現(xiàn)分量，此時成為弱磁狀態(tài)，即永磁體產(chǎn)生的磁場被??產(chǎn)生的磁場削弱了，進而在同樣的電壓下能夠產(chǎn)生更高的轉速。

Source: Dr. Galea

上面討論的是??（即隱極）的情況，當??時，電壓方程變?yōu)椋?/p>

電壓極限圓變成了電壓極限橢圓，如下圖所示：

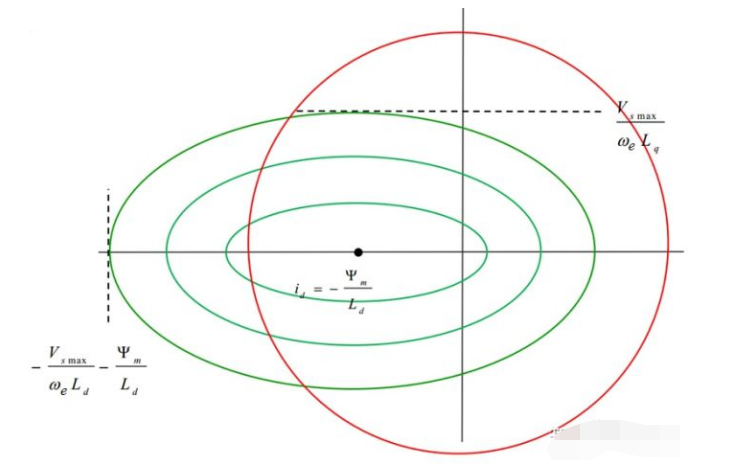
Source: Dr. Galea

當電機做好之后，?，因此任意的??、??都會對應一個力矩值，我們把力矩相同的之用線連起來就得到一族等力矩曲線，如下圖的三條黑色的等力矩線。

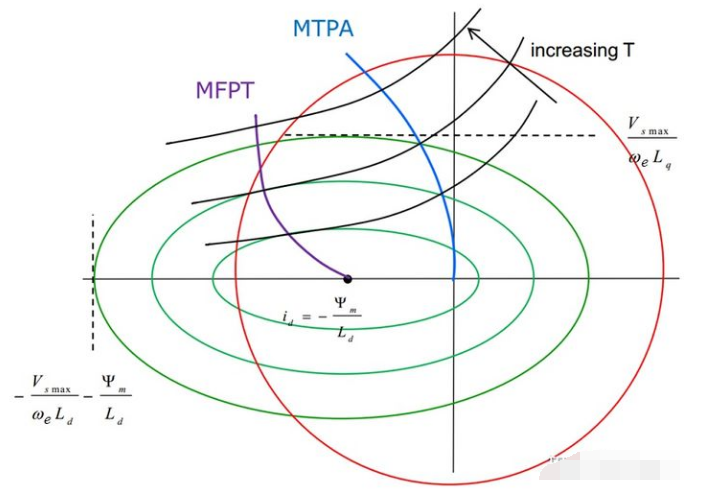
Source: Dr.Galea

同一個等力矩的曲線會和不同的電流圓相切，產(chǎn)生一系列的切點，這些切點的軌跡就是MTPA（最大力矩比電流）控制點，因為在一定的電流極限下，該切點是力矩最大的點。

同一個等力矩的曲線會和不同的電壓橢圓相切，產(chǎn)生一系列的切點，這些切點的軌跡就是MFPT（最大轉速比力矩）控制點，因為在一定電壓極限（電壓代表著速度）下，該切點是速度最大的點。

七、旋轉磁場是如何產(chǎn)生的

前面我們說了這么多，都有一個大前提：電機要連續(xù)旋轉 ，一定要有一個旋轉的磁場。那旋轉磁場從何而來？

說到這我們不得不提一個人——尼古拉·特斯拉，關于特斯拉，有很多傳說：

有人說，他預測出第一次、第二次世界大戰(zhàn)；

有人說，他預見了泰坦尼克號的沉沒；

有人說，他制造了通古斯大爆炸，威力是廣島核彈的1000倍；

有人說，他可以利用電磁，穿越時空；

有人說，F(xiàn)BI將他的照片掛在機密大樓的頭號位置。

2003年，一個叫馬斯克的科技狂人，創(chuàng)辦了一家很酷的電動汽車企業(yè)，取名特斯拉。正是為了致敬他的偶像：尼古拉·特斯拉。今天我們就從一個小角度，來窺探一下特斯拉的偉大之處——交流電。

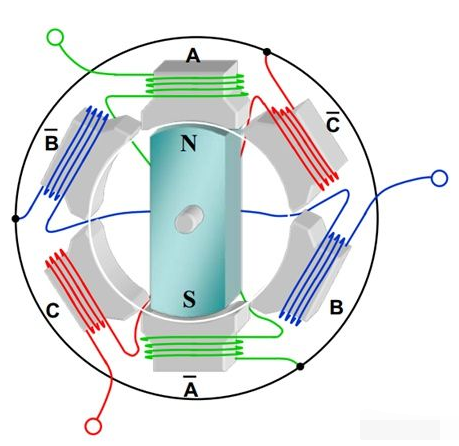
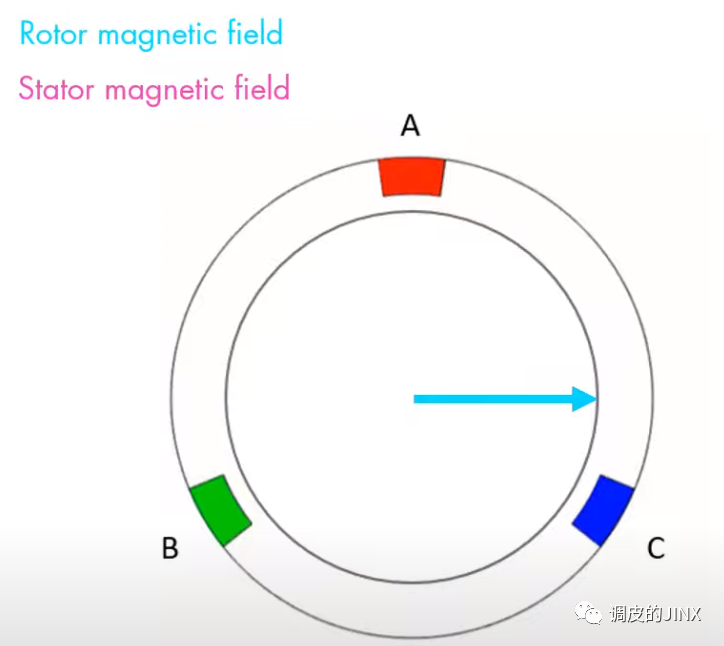
一個典型的永磁同步電機的繞組如上圖所示，3相繞組在空間120°電角度布置，繞組里面分別通相位相差120°的三相交流電：

那繞組中產(chǎn)生的磁動勢是什么樣子呢？

化簡一下：

如果你還沒看出來，我們用圖像來演示一下前面的推理過程，可能會更形象一些：

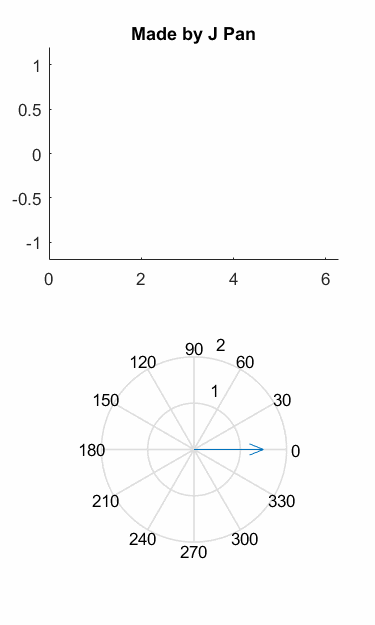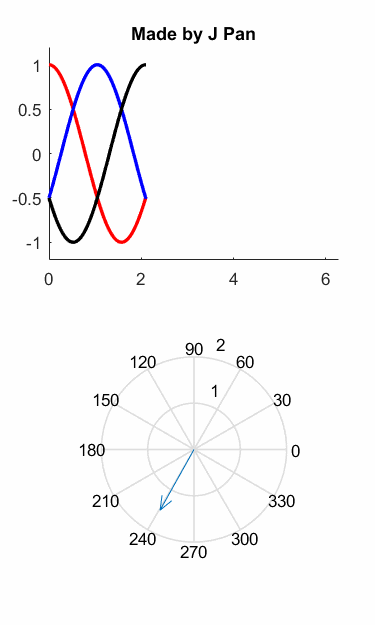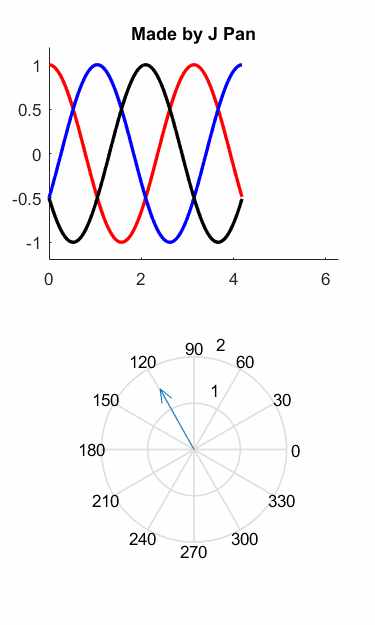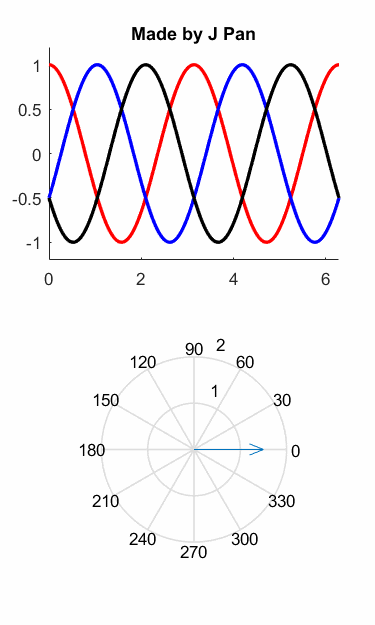
也就是說，磁動勢變成了一個旋轉的矢量！

如果把坐標系放在電機里面，大概是這個樣子：

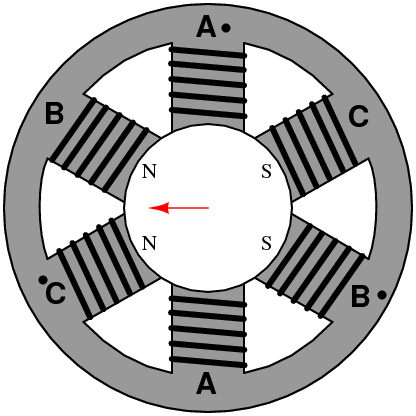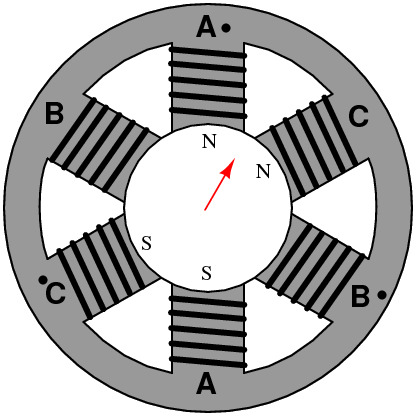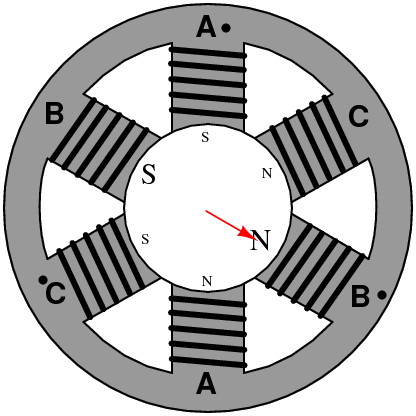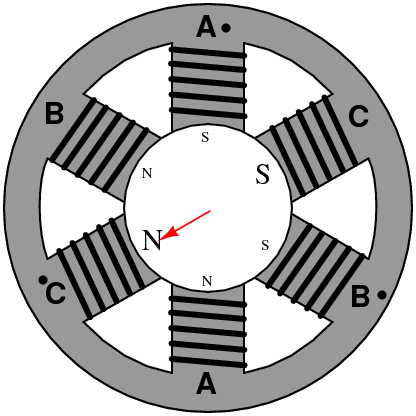
好了，現(xiàn)在旋轉的磁場已經(jīng)產(chǎn)生了，它的表達式是這樣：

那么新的問題來了，大多數(shù)人數(shù)學不好啊，不會復數(shù)計算啊，怎么辦？這時候大神歐拉來了，用我的公式啊——好用，最主要還是免費的：

合成磁動勢是一個復數(shù)，我們可以用歐拉公式轉換一下：

也就說合成磁動勢可以由兩個空間和相位都差90°的諧波組成。

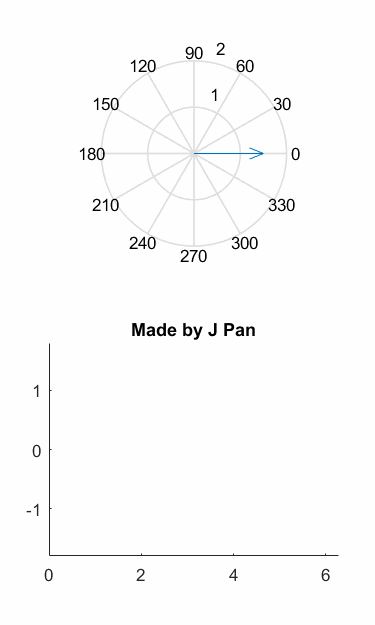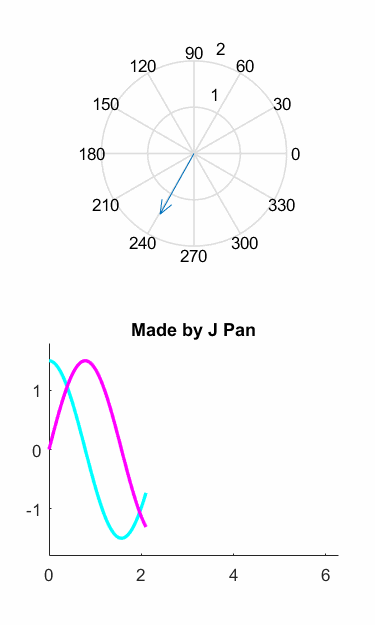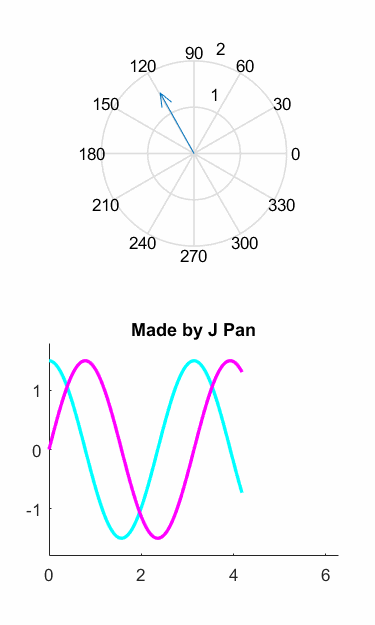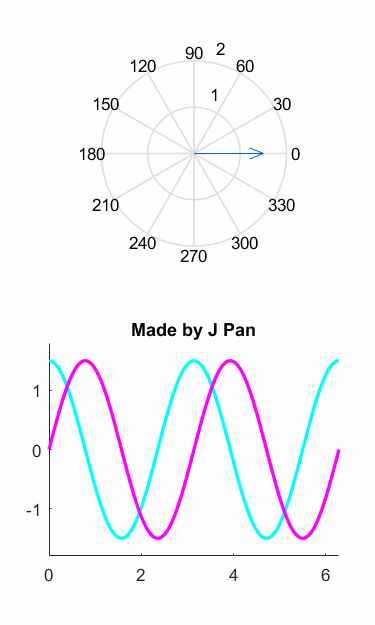
整理一下思路：我們有一個三相繞組，空間和相位都差120°，合成起來是一個旋轉的磁動勢，公式簡潔漂亮，可是不好計算。我們用歐拉公式轉換一下，發(fā)現(xiàn)用一個空間和相位都差90°的亮相繞組可以完美等效,這就是Clark變換。

好了，現(xiàn)在我們有一個旋轉的磁場了，也知道怎么等效計算了，但是感覺還是太復雜，我們能不能再偷點懶了？——如果我們站在一個坐標系里面，這個坐標系也在旋轉，而且旋轉的速度和合成磁動勢一樣，這時候再去觀察磁動勢，會是什么樣？——一個常量，這就是Park變換。

編輯：黃飛