1?背景描述
Ansys Maxwell高性能計算技術可幫助用戶提高仿真效率,求解更多設計方案、洞察更多設計空間,同時幫助用戶創建更準確的ROM。高性能計算包含DSO/LS-DSO、HPC、TDM、DDM等。
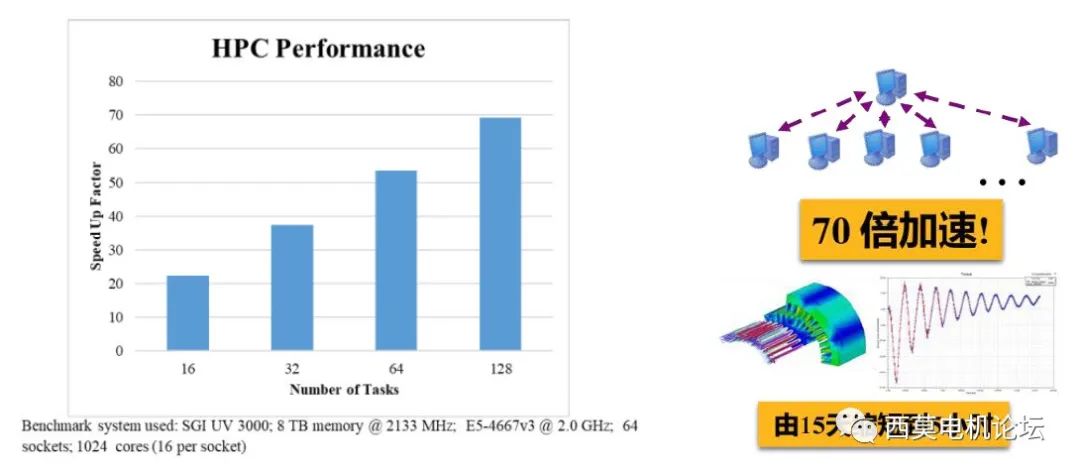
高性能計算
其中DSO/LS-DSO是高效、可擴展、分布式的并行計算解決方案,HPC可以多線程處理大型3D問題,DDM是3D渦流場求解器基于MPI的域分解法,可以對3D渦流場求解器GPU進行加速,而TDM支持如下幾種情況:
(1)同時求解多個時間步
(2)普通瞬態
(3)周期性&半周期性
(4)使用TDM求解3D瞬態場源-目標鏈接。
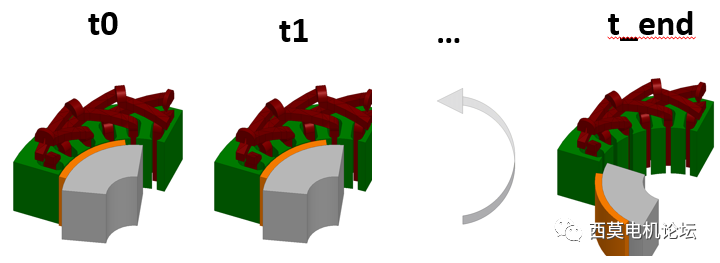
TDM求解
2 TDM功能介紹
TDM(Time Decomposition Method)時間分解法是一種高性能分布式計算的方法,它基于沿時間軸的時域分割來并行計算瞬態場問題,而不是幾何分割。
TDM不同于Maxwell常規瞬態算法,它不是順序求解各個時間步,而是多個時間步同時求解。
TDM可以使用在基于MPI的分布式內存并行平臺上。
TDM具有非常好的可擴展性,可以明顯加速2D和3D瞬態場問題的求解。
常規瞬態求解算法是按序求解所有的時間步,如下圖所示。
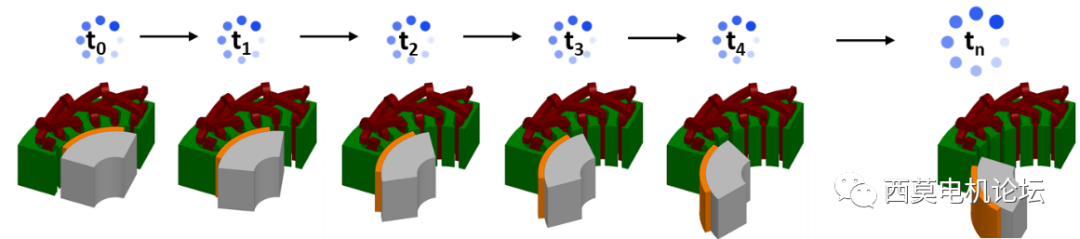
常規瞬態求解算法
而TDM 瞬態求解算法是同時求解所有的時間步,如下圖所示。
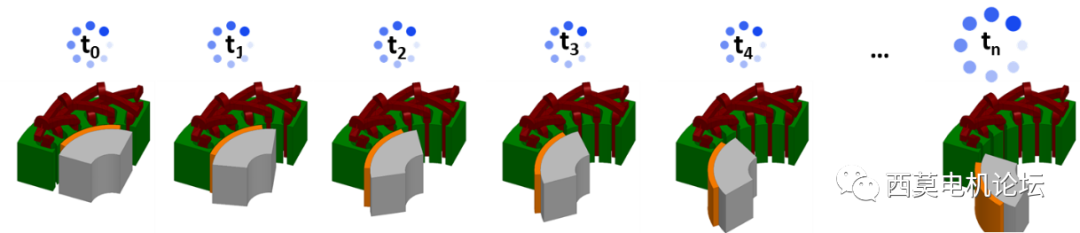
TDM 瞬態求解算法
TDM求解算法中關于Sub-division子時間段的原理圖如下圖所示。
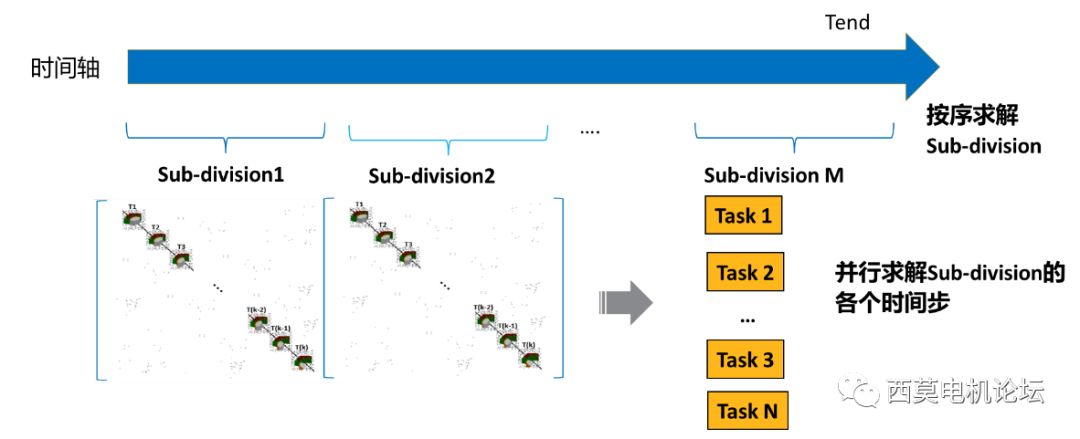
Sub-division子時間段
使用TDM需要進行兩處設置,分別是HPC設置及TDM設置。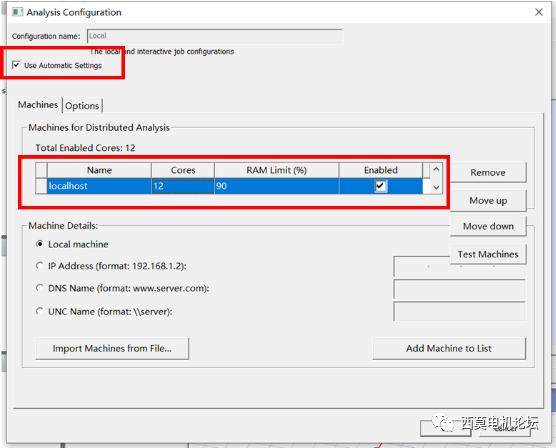
HPC設置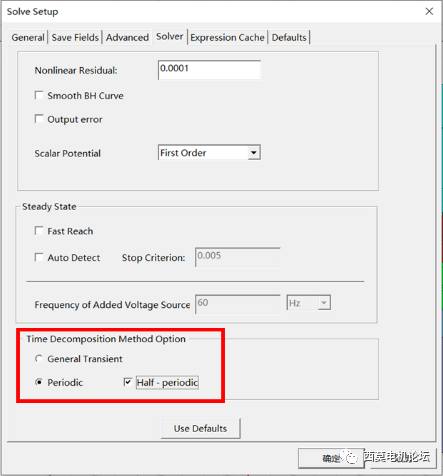
TDM設置
HPC設置方法:首先勾選Use Automatic Settings,通過Num variations distribute設置TDM并行掃參數,Cores用于設置調用的核心數,最大可設置為邏輯處理器核心數。
建議用戶按如下推薦進行設置:
協調Timesteps和Cores
使Timesteps/(Cores-1)=整數
由于PeriodicTDM同時對所有時間步進行求解,因此必須確保可用內存大于每個時間步消耗內存*時間步數,并留20%左右余量。

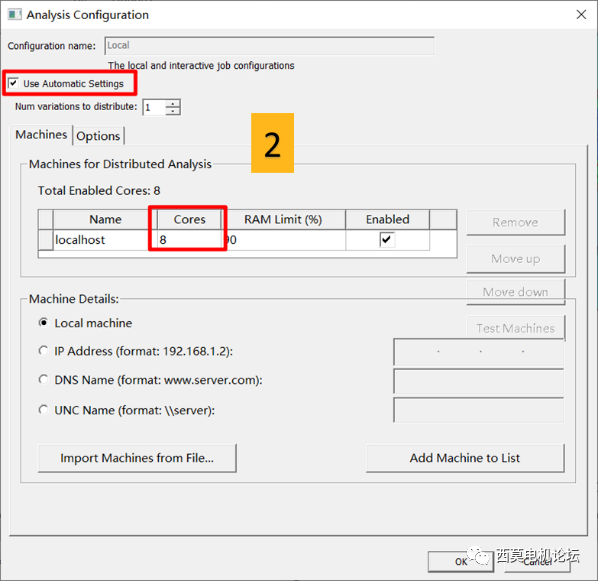
HPC參數設置
TDM有兩個選項,包含General Transient常規瞬態求解和Periodic周期性模型。General Transient 常規瞬態求解支持任意的瞬態模型,該方法是最靈活的方法,同時支持渦流效應,可以同時使用快速達到穩定設置“fast reach steady state”。
Periodic周期性模型可以直接達到瞬態穩定狀態,如果求解是周期性的,可以使用分布式任務求解一個完整的周期(而且只需要求解一個)。
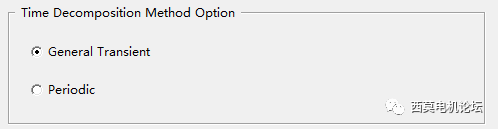
TDM選項
TDM包含周期/半周期TDM。周期TDM設置仿真時間為一個或多個周期,軟件只需計算一個周期,直接輸出所有周期結果,并直接達到瞬態穩態,典型應用是同步電機的短路分析,感應電機堵轉分析。
半周期TDM設置仿真時間為半個周期,軟件只需計算半個周期,直接輸出一個完整周期結果,典型應用是快速計算同步電機的穩態工況。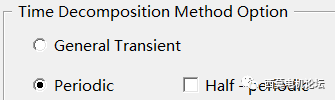
周期TDM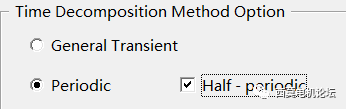
半周期TDM
周期性TDM的限制條件有如下幾點。
首先是關于外電路。
由于TDM算法需要同時求解子時間步集合,如果外電路中的PWM波的開關策略要基于歷史時間步下的電流結果的話,對于TDM求解器來說,激勵源在不同時間步時是未知的,所以這種情況不支持TDM功能,但是如果開關策略是基于時間或位置,則是可以應用TDM功能。
其次是關于機械瞬態。
TDM 不支持機械瞬態,因為TDM必須事先知道每個時間步的移動位置,以便FEA求解器在該預定位置執行計算,機械瞬態顯然無法滿足這一點。
再次是關于鐵損計算。
一個時間步的解不能依賴于幾個時間步以前的歷史時間步的解(由于時間積分算法自身需要,允許前兩個時間步解)。常規的鐵損計算是支持的,因為常規的鐵損計算是在后處理中完成的。嚴格來說是不支持磁滯模型,但是對于電機硅鋼片這類軟磁材料,由于磁滯效應較弱,求解器采用了解耦算法,使TDM支持這種應用,但計算結果與常規算法有一定誤差。
最后是關于退磁。
永磁體退磁分析的目的是在瞬態場分析中找到整個瞬態過程中最惡劣的工作點,每當發現新的最惡劣工作點后,軟件將使用線性表示的永磁特性來構建新的回復線,該回復線應用于后續時間步的仿真。
因此嚴格來說,TDM不支持退磁模型,因為TDM必須同時求解某個時間步子集。但是,作為一種合理的近似方案,我們可以基于分布式并行的TDM同時求解某個時間子集,然后在這些已求解的時間步中找到最惡劣的工作點,進一步,最惡劣工作點用于構建一條新的回復線,該回復線用于下一個時間子集的計算。
這意味著找尋最惡劣工作點這項工作是在逐個時間子集中進行的,而不是像在常規計算那樣在逐個時間步中進行的。因此通過這種方法找到的最惡劣工作點會與常規計算時有一些不同。但是,從實際應用的角度來看,該解決方案可以被認為是足夠準確的。為了盡可能減少誤差,可以減少一個時間子集中的時間步數。
3??TDM在永磁電機仿真中的應用
開路和穩態短路分析是永磁同步電機的重點仿真項目,利用Maxwell中的Periodic TDM和Half-Periodic TDM功能,可大幅降低計算量,縮短仿真時間。提高仿真效率。
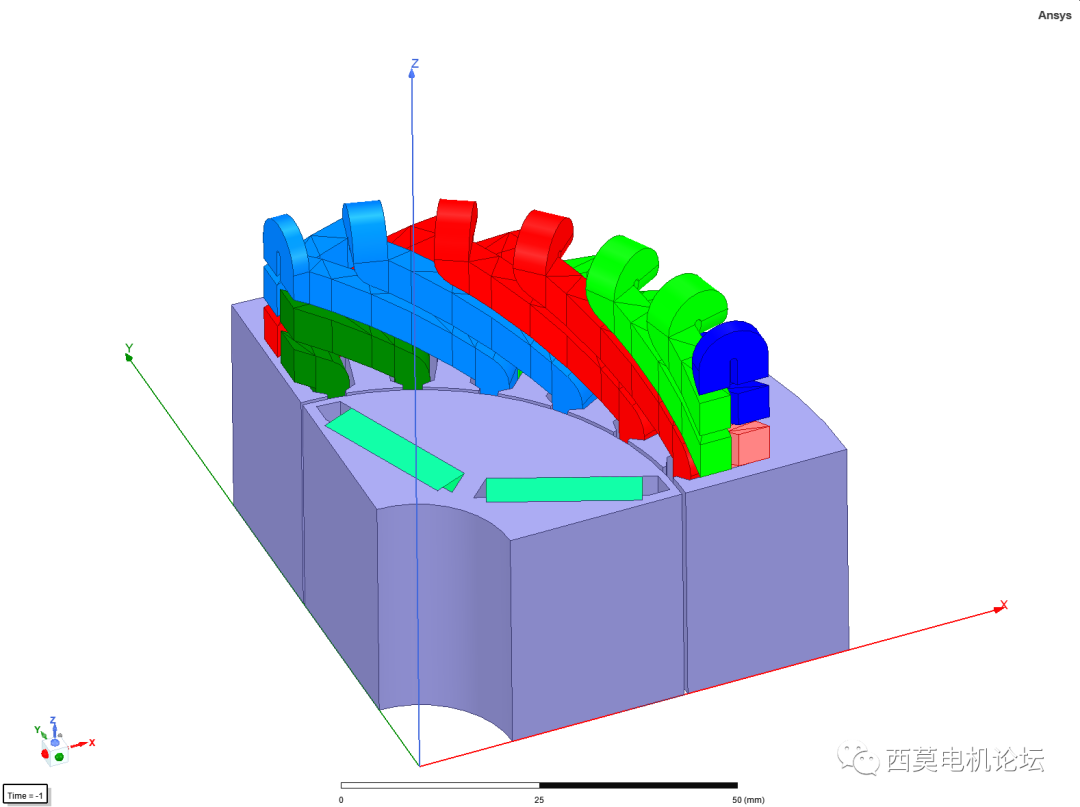
永磁同步電機
首先進行穩態短路分析,采用PeriodicTDM。在Setup>>Sovler處勾選Periodic,本例中電機極數為4極,Stop Time設置為1個電周期,每個電周期30個時間步,實際計算30個時間步。
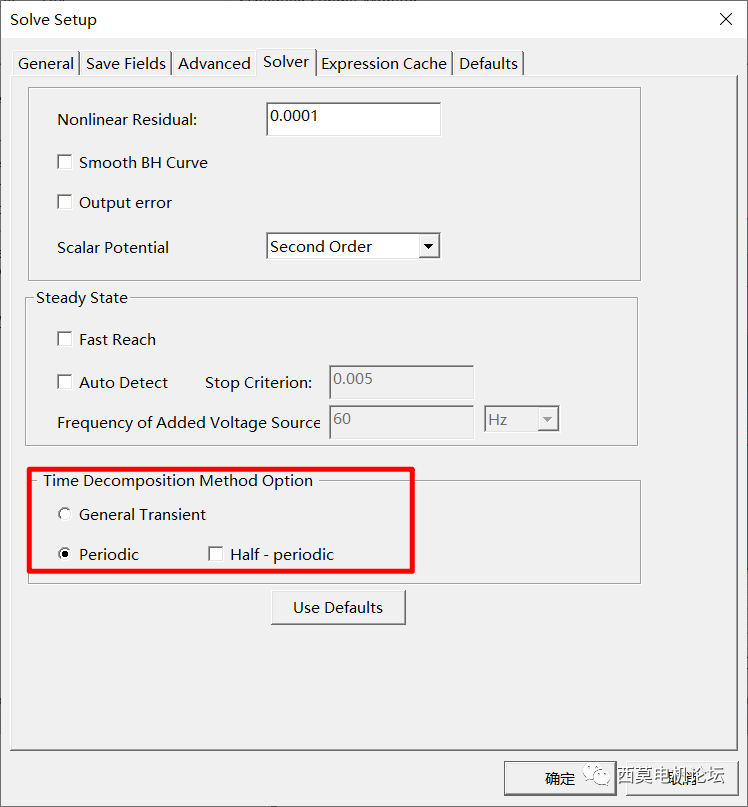
勾選Periodic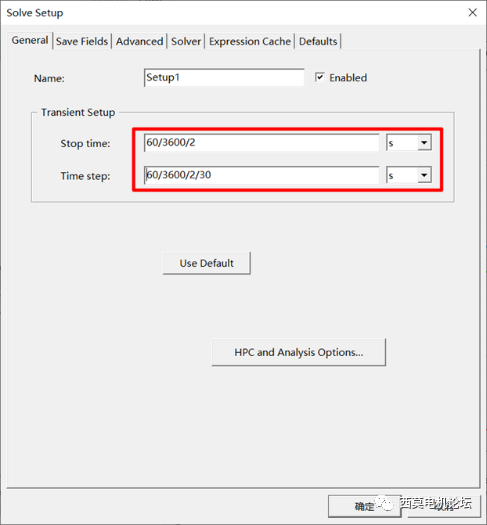 ?
?
設置計算時間及時間步長
若采用常規方法計算,需要200電周期以上才能穩定,而采用周期TDM,只需1個電周期達到穩定,求解器跳過瞬態迭代過程,直接輸出穩態短路電流,求解30個時間步總時間為17分鐘。

網格剖分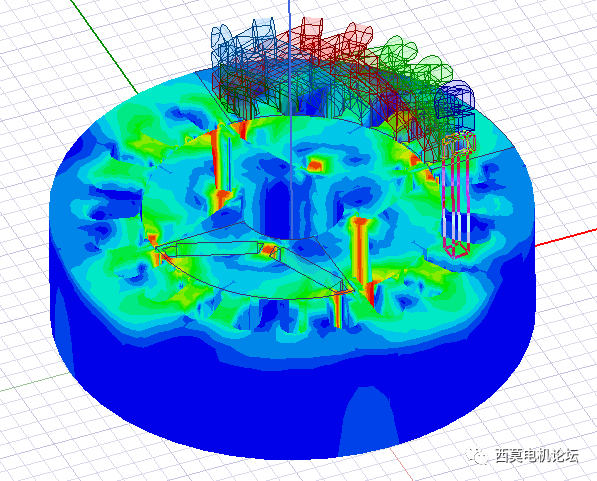
磁密云圖
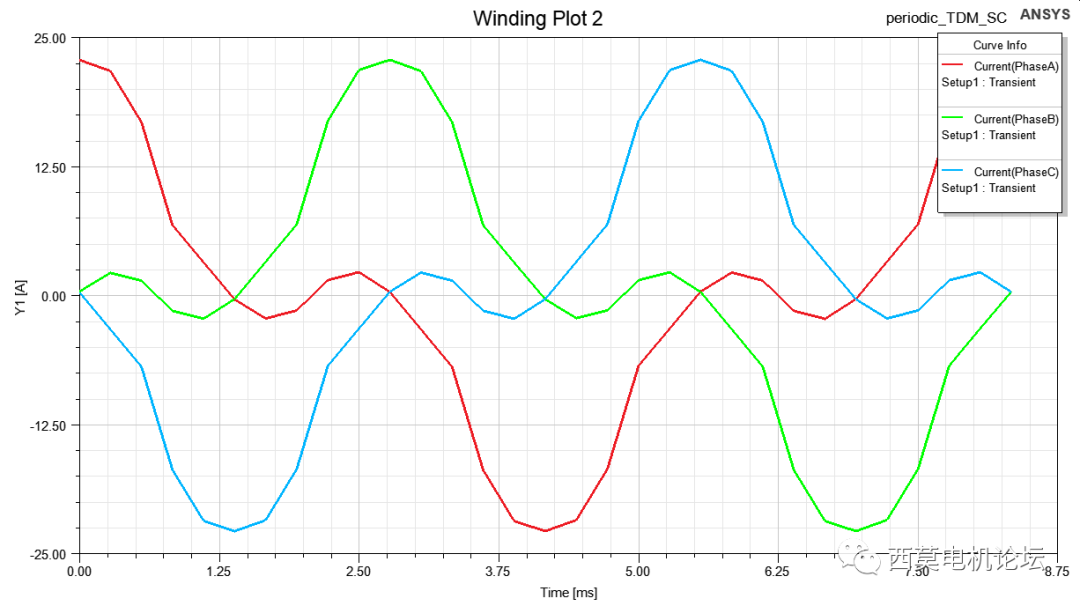
穩態短路電流
用戶需要注意的是本例同樣適用于Half-Periodic。
接著進行開路分析,采用Half-PeriodicTDM。在Setup>>Sovler處勾選Half-Periodic,采用Half-Periodic求解時,求解模型需符合反對稱周期特性,本例中電機極數為4極,Stop Time設置為半個電周期,每個電周期采用60個時間步,實際計算30個時間步。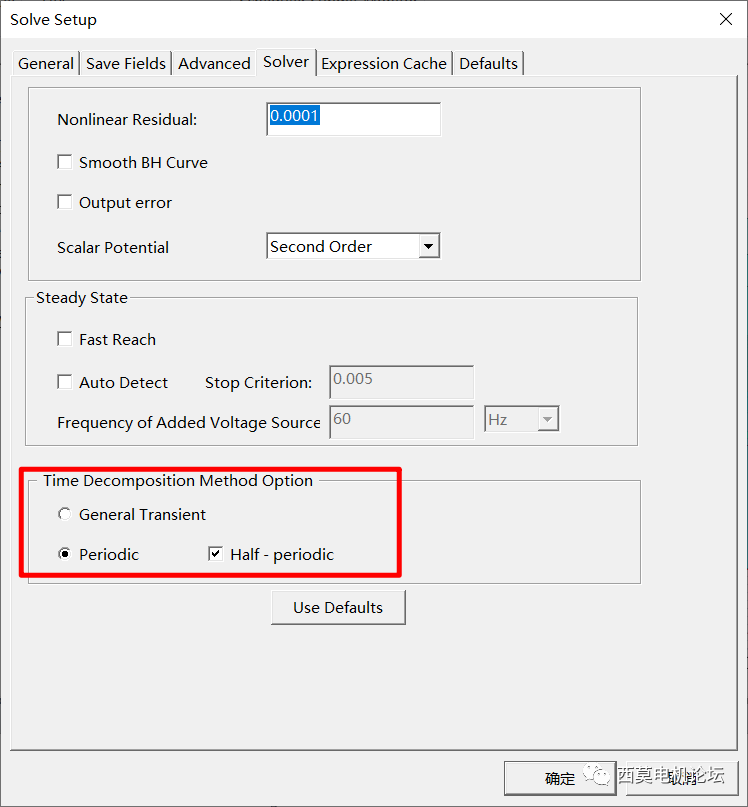 ?
?
勾選Half-Periodic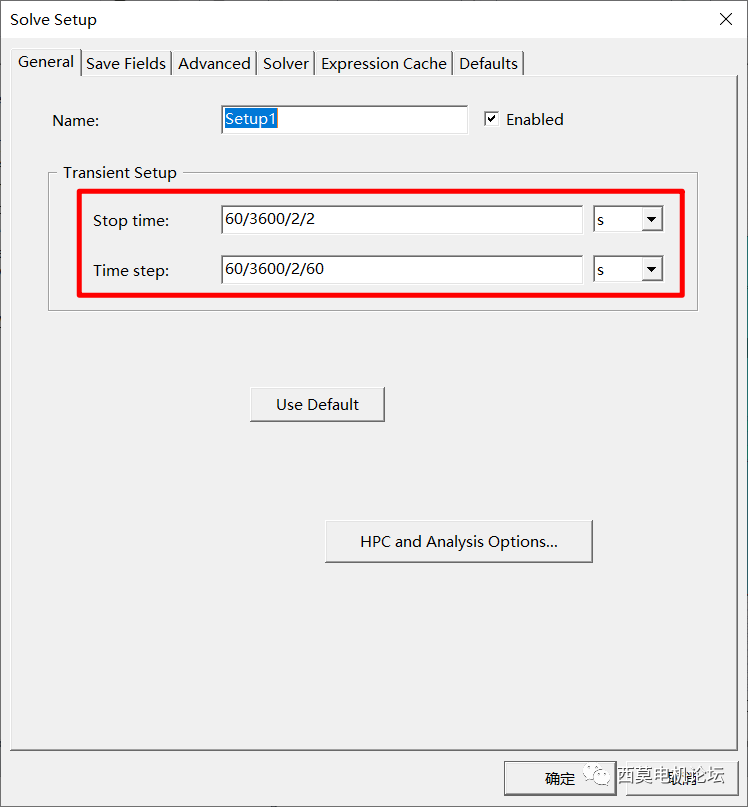 ?
?
設置計算時間及時間步長
常規計算鐵損至少需要一個半周期,采用半周期TDM,僅需計算半個周期,即可輸出完整周期鐵損、反電勢波形,本例求解30個時間步時間為7m30s。
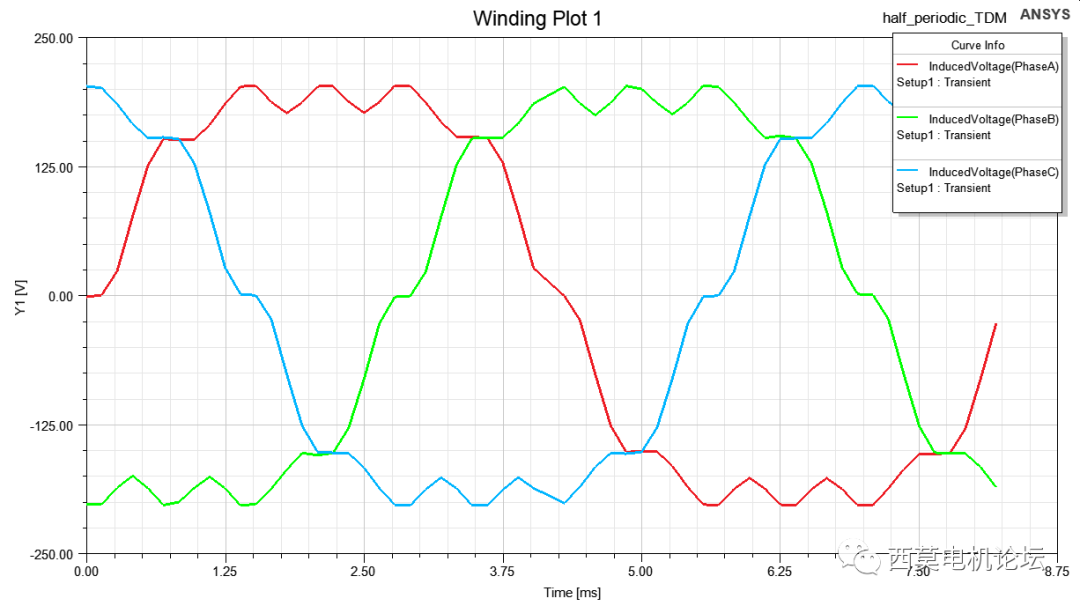
反電勢結果
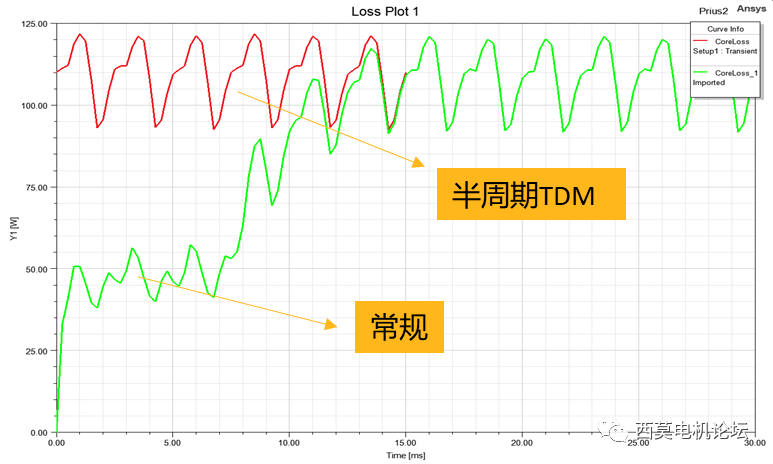
鐵損結果
各方案計算的總耗時及反電勢結果見下表所示。
| 方案 | 計算時間 | A相反電勢rms值/V |
| 無TDM | 36m50s | 159.98 |
| 常規TDM | 17m44s | |
| 周期TDM | 14m52s | 161.08 |
| 半周期TDM | 7m30s |
從上述結果可知,半周期TDM耗時最短,僅為7m30s,計算精度高。
4 TDM在感應電機仿真中的應用
堵轉仿真在感應電機分析中比較常見,通常用于計算其堵轉轉矩和堵轉電流,校核電機起動性能。若采用常規分析方法,即使開啟Fast Reach和Auto Detect功能,也需要幾十個周期才能收斂,這將花費很長的計算時間,若使用周期TDM可以一個周期直達穩態,可以大幅降低求解計算量,提高仿真效率。
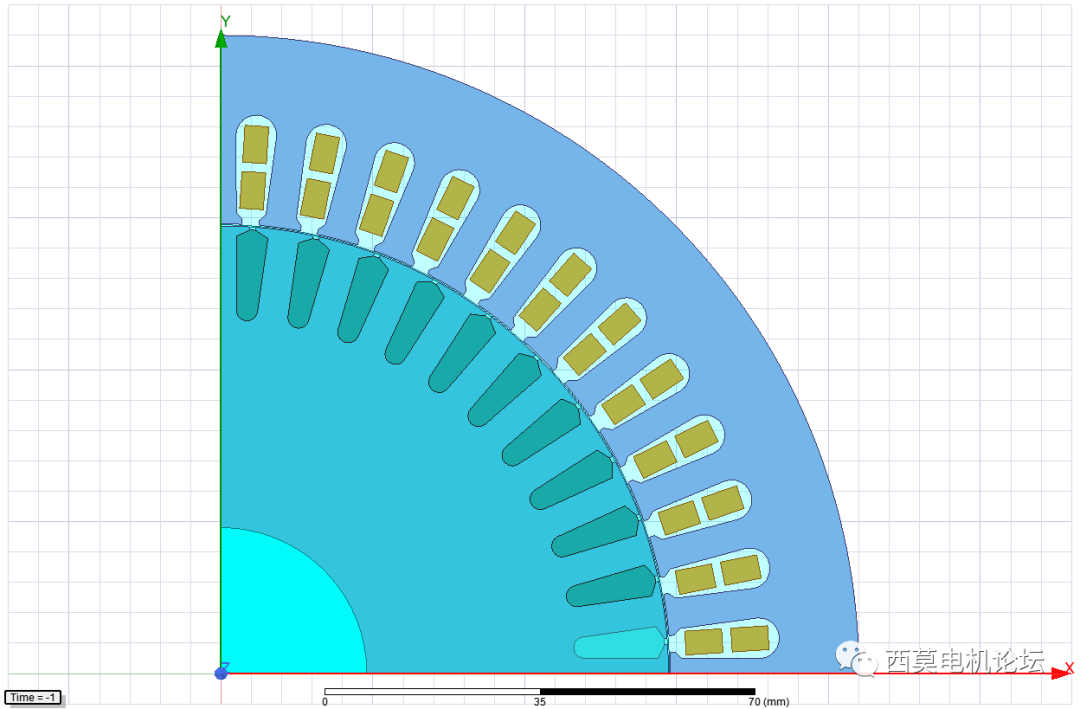
感應電機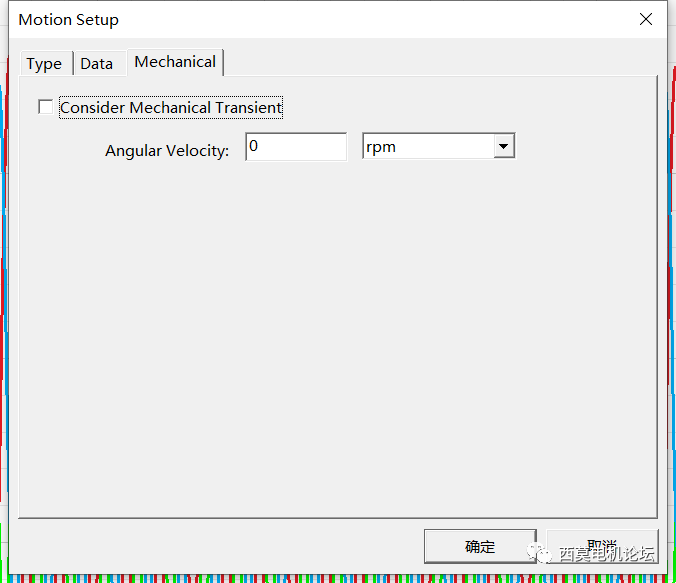
堵轉仿真
首先測試不使用TDM,單核計算單任務,設置如下。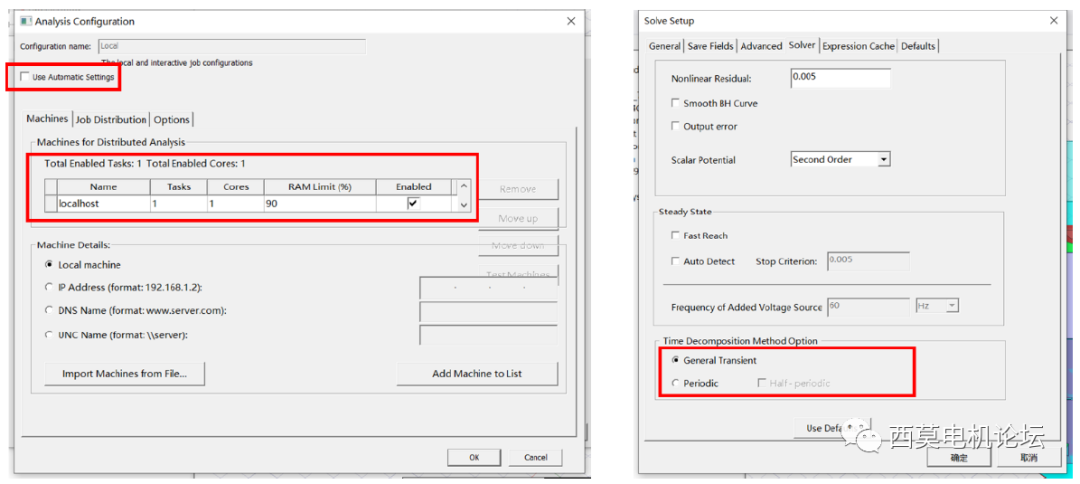
不使用TDM
仿真40個電周期后轉矩趨于穩定,計算時間耗時3min48sec。
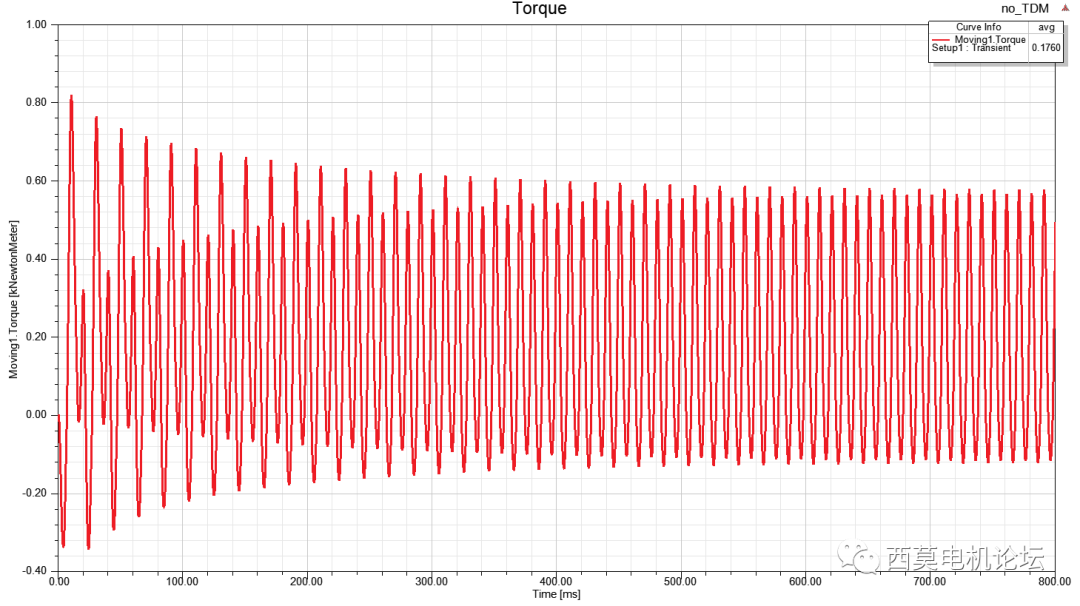
轉矩vs時間
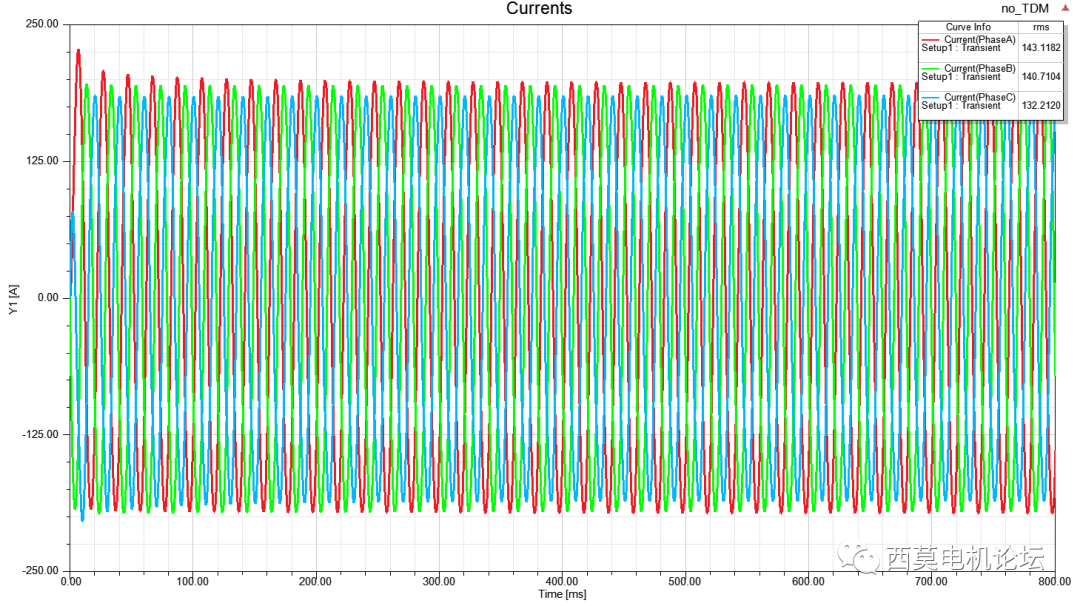
電流vs時間
接著測試使用周期TDM進行計算,設置如下。 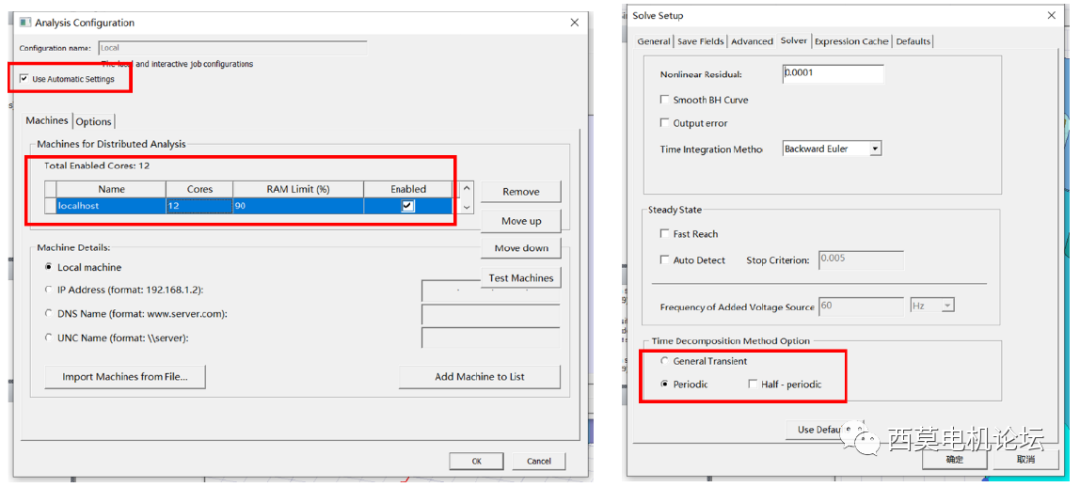
使用周期TDM
只需仿真一個電周期,即可直接達到穩態,計算耗時0min57sec。
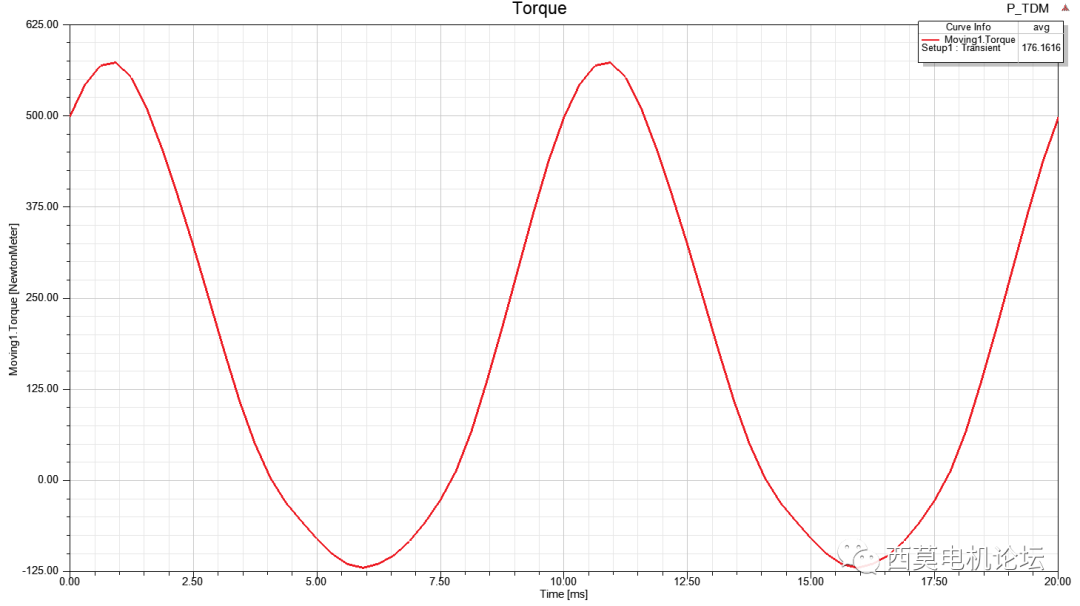
轉矩vs時間
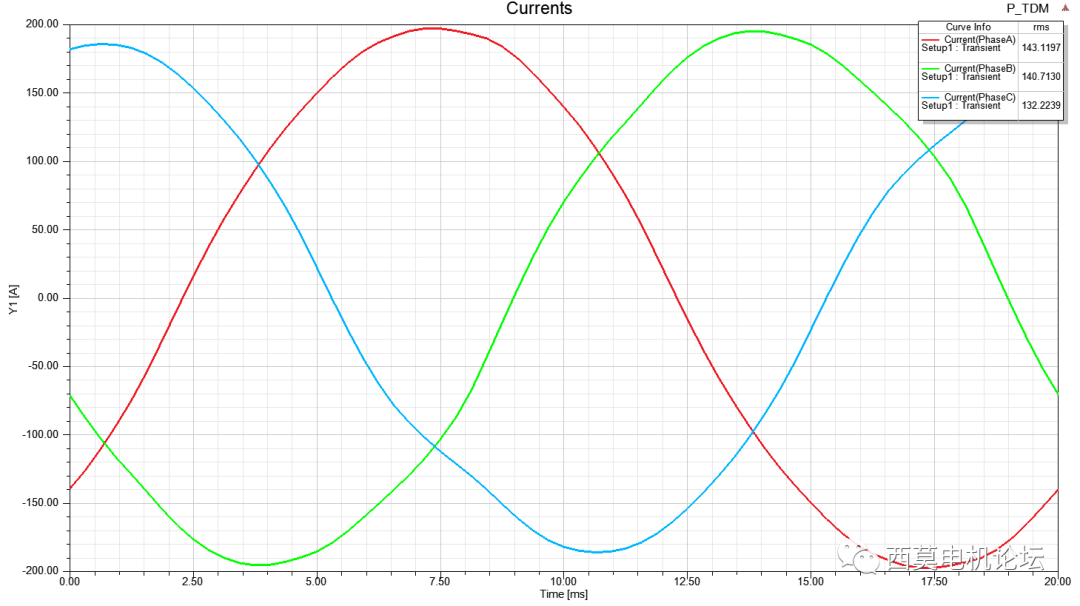
電流vs時間
最后測試使用半周期TDM進行計算,設置如下。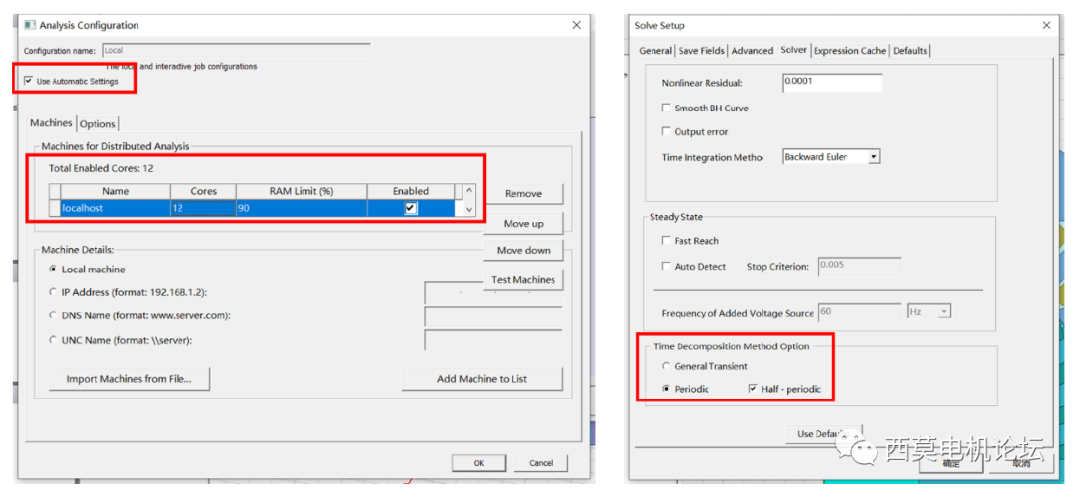
使用半周期TDM
只需仿真半個電周期,軟件自動給出穩定后一個完整電周期的結果,計算耗時0min21sec。
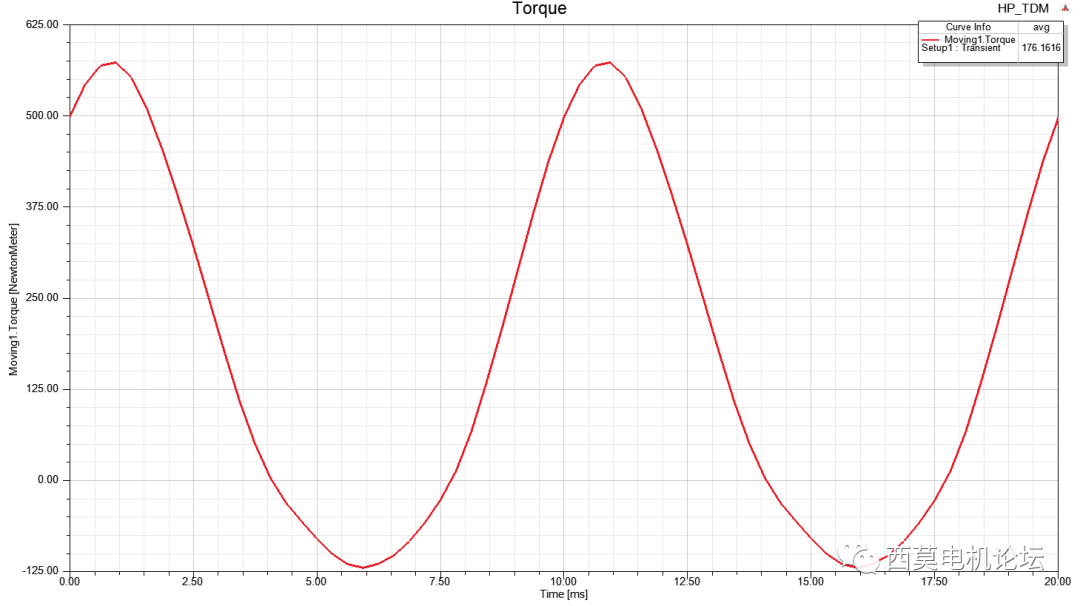
轉矩vs時間
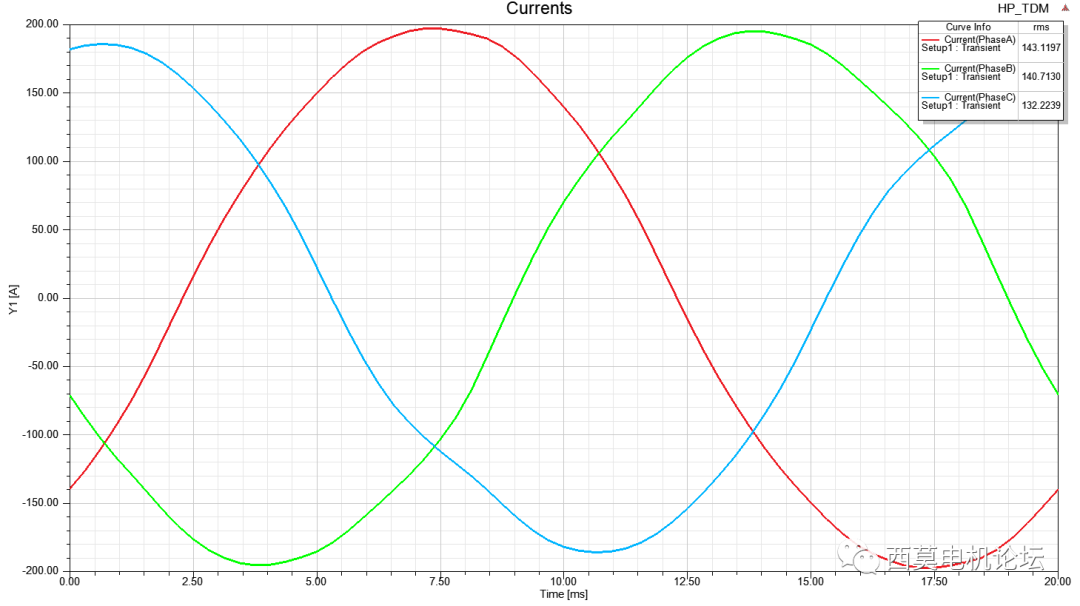
電流vs時間
四種計算方法所用計算時間及轉矩與電流值結果如下表所示。
| 計算方法 | 計算時間 | 轉矩平均值/Nm | A相電流rms值/A |
| 無TDM | 3m48s | 176.0478 | 143.1182 |
| 常規TDM | 4m36s | ||
| 周期TDM | 0m57s | 176.1616 | 143.1197 |
| 半周期TDM | 0m21s |
從結果可以看出,正常順序求解和常規TDM計算時間相近,而利用周期性TDM功能可大幅降低感應電機堵轉工況仿真時間,且精度可靠。
周期性TDM與無TDM計算的堵轉電流與堵轉轉矩結果對比見下圖所示。
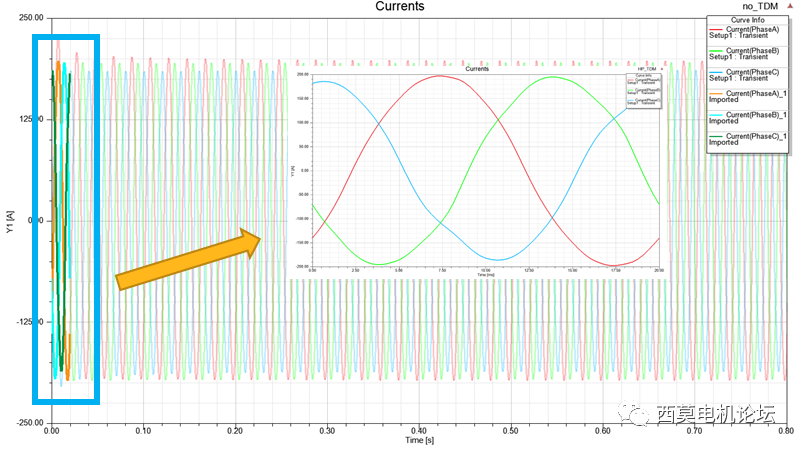
堵轉電流
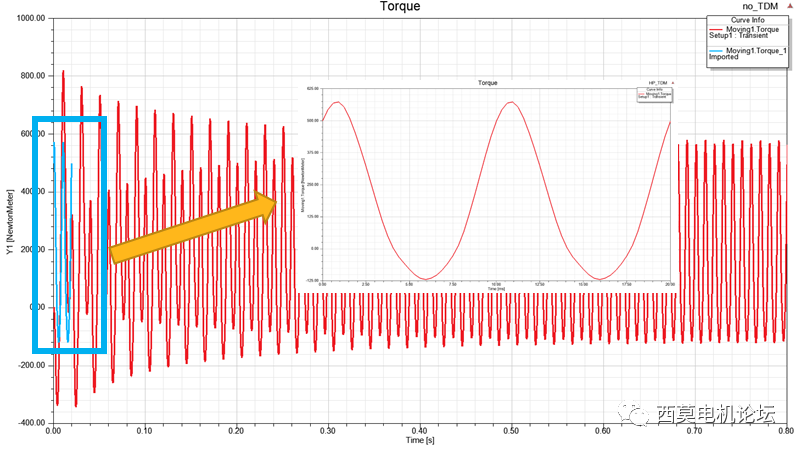
堵轉轉矩
當案例中有參數化掃描需求時,周期性TDM方式具有非常大的優勢。以一轉子初始位置角度進行掃描為例,對比不同TDM計算方式總時間。常規TDM與周期TDM計算的轉矩結果見下圖所示。
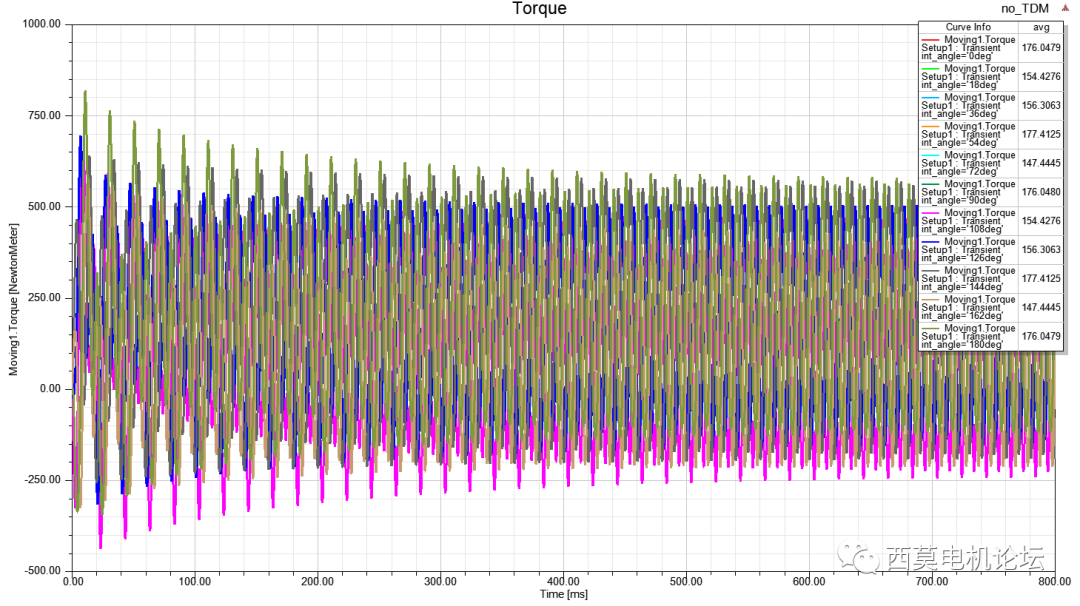
常規TDM
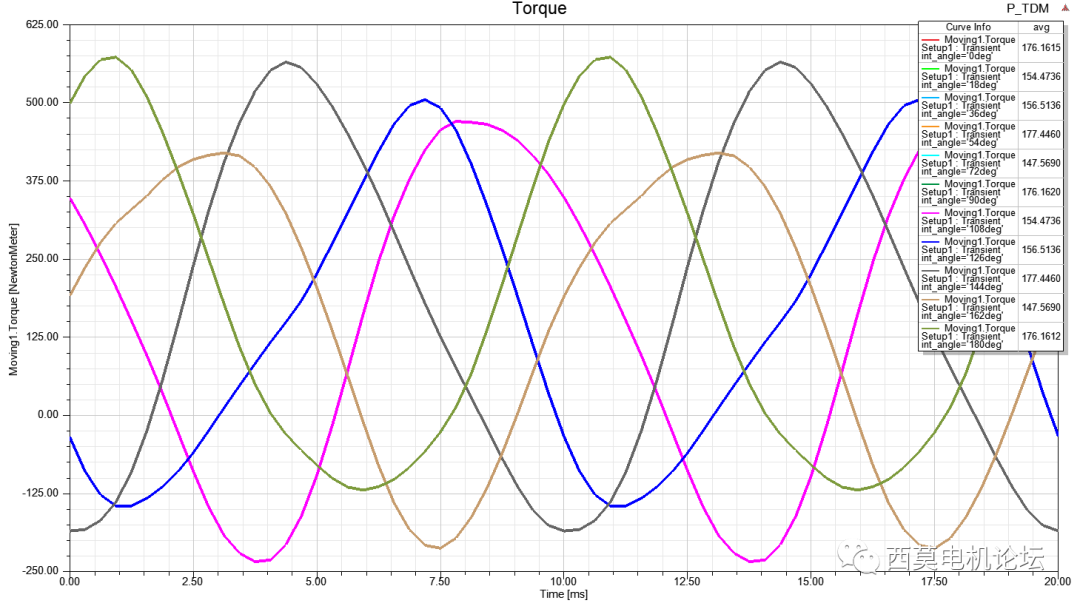
周期TDM
計算時間對比如下表所示。
| 計算方法 | 計算時間 |
| 常規TDM(40個電周期) | 1h16m49s |
| 周期TDM | 13m18s |
| 半周期TDM | 6m40s |
從結果可以看出,當采用常規TDM時,由于無法預測各初始位置角時達到穩態所需時間,本例中統一采用40個電周期進行計算,然而某些初始位置角達到穩態的時間可能小于或者大于40個電周期,在這種情況下,準確評估電機堵轉性能有較大困難。當采用周期性TDM時,程序直接給出穩定后的仿真結果,這極大縮短了總體仿真時間
因此,當案例中有參數化掃描需求時,周期性TDM求解方式具有非常大的優勢。
5 TDM在ECE提取中的應用
在Maxwell有限元場計算中,有限元模型對電流和轉子位置角掃描,掃描后得到的有限元結果通過降階模型保存在數據表中形成ECE模型,可將ECE模型直接在Simplorer(Twin Builder)進行分析計算,也可以將ECE模型送到控制當中進行高級控制系統仿真。
等效抽取的結果是基于有限元計算得到的數據表,在控制系統聯合仿真過程中只需通過查表的方法就能得到電機的性能,因此將抽取后的結果應用到系統仿真中,既保證了精度也提高了速度。
接下來分別測試兩個模型,分別是少單元數模型和中等單元數模型。
首先是少單元數模型,系統參數及模型參數信息如下:
操作系統:Windows7
軟件版本:MaxwellR19.0
可用核數:10個物理內核(若使用超線程,20個虛擬內核)
測試模型:Prius 2DMotor
單元總數:1634
總數據點數:13671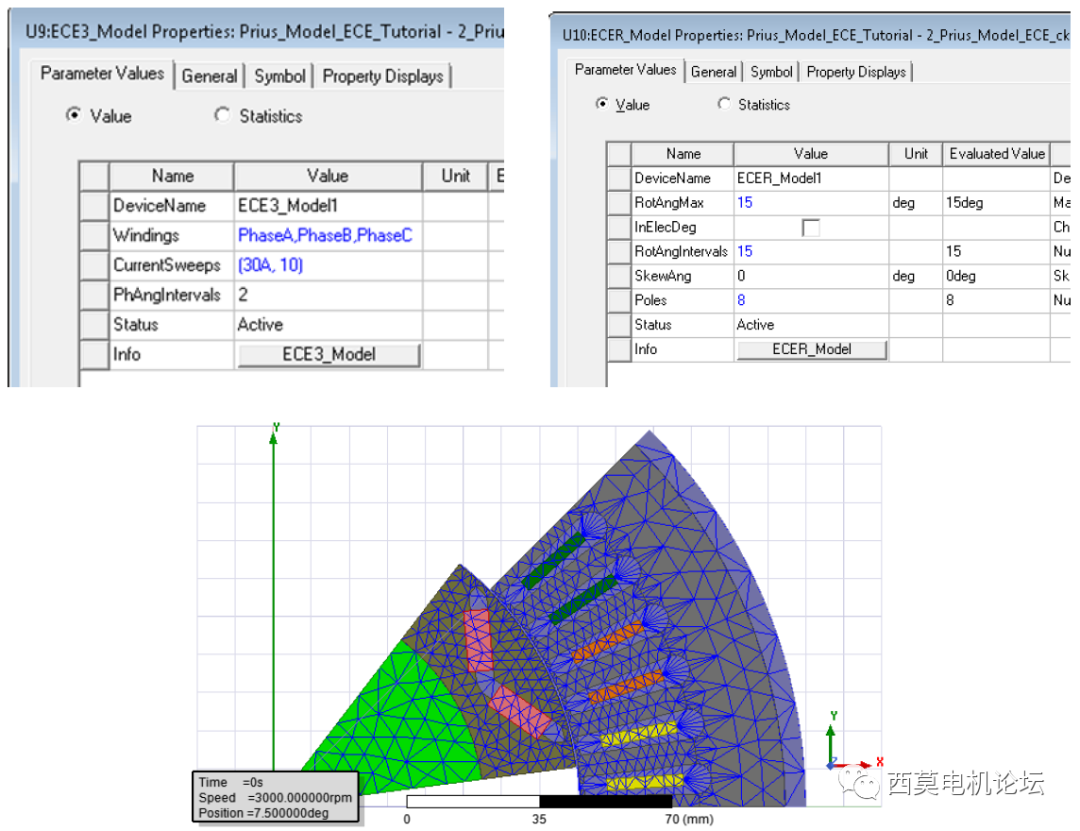
少單元數模型(1634單元數目)
計算耗時結果如下表所示。
| HPC Setting | Cores | Time/min | Time % |
| NON | 1 | 79 | 100 |
| TDM - Auto | 2 | 85 | 108 |
| TDM- Auto | 4 | 39 | 49 |
| TDM- Auto | 8 | 28 | 35 |
| TDM- Auto | 16 (hyperthreading) | 36 | 46 |
| Regular HPC | 16(hyperthreading) | 82 | 104 |
接下來是中等單元數模型,系統參數及模型參數信息如下:
操作系統:Windows7
軟件版本:MaxwellR19.0
可用核數:10個物理內核(若使用超線程,20個虛擬內核)
測試模型:Prius 2DMotor
單元總數:16286
總數據點數:13671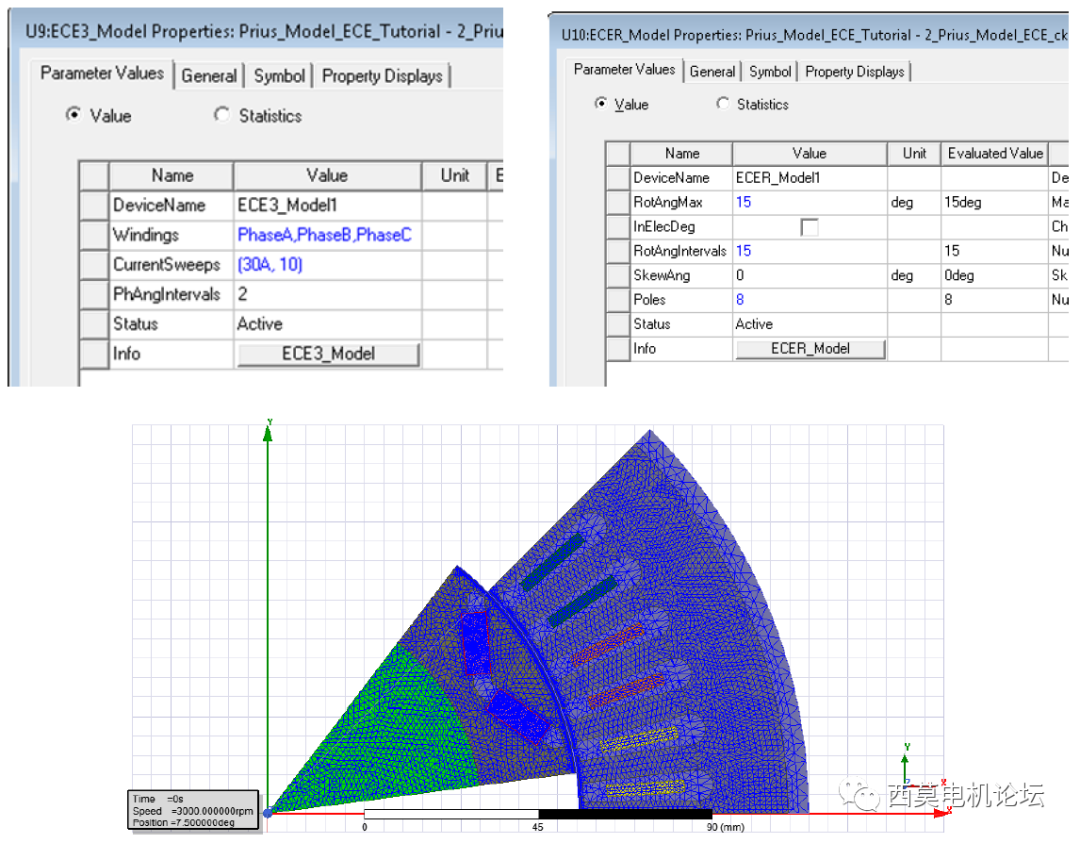
中等單元數模型(16286單元數目)
計算耗時結果如下表所示。
| HPC Setting | Cores | Time/min | Time % |
| NON | 1 | 347 | 100 |
| TDM - Auto | 2 | 361 | 104 |
| TDM- Auto | 4 | 312 | 90 |
| TDM- Auto | 8 | 149 | 43 |
| TDM- Auto | 16 (hyperthreading) | 110 | 32 |
| Regular HPC | 16(hyperthreading) | 360 | 104 |
6?總結
TDM時間分解法是一種高性能分布式計算的方法,它基于沿時間軸的時域分割來并行計算瞬態場問題。TDM主要優點總結如下:
(1) TDM可以實現多時間步的并行求解,充分利用計算機資源;
(2) 周期TDM對于同步電機穩態短路工況仿真只需一個周期即可收斂,大幅降低計算量;
(3) 周期TDM對于同步電機正常穩態工況也有價值,減少鐵損計算周期數;
(4) 周期TDM對于感應電機堵轉工況的快速收斂有極大的幫助;
(5) TDM可大幅提高電機ECE模型提取速度。
總之,TDM時間分解法可幫助用戶提高仿真效率,求解更多設計方案、洞察更多設計空間,同時幫助用戶創建更準確的ROM。
審核編輯:劉清
 電子發燒友App
電子發燒友App





















評論