在學習FOC控制前,我對于FOC控制完全不懂,只知道中文叫做磁場定向控制,因公司產品開發需要用到對永磁同步電機(PMSM)進行精確的位置控制,才開始從網上了解什么是FOC,有哪些數學公式,控制的過程是怎么樣的,但由于公司沒有人知道這一塊的知識,所以只能一個人慢慢找資料學習,網上有不少關于FOC的資料,不過講的都不全面,而且有的還會存在錯誤,但是不懂的時候也無法分辨對錯,所以走了不少彎路。所以將個人的學習心得記錄于此,與大家分享,由于需要對電機進行位置控制,所以使用了14位分辨率的磁編碼器。
FOC主要是通過對電機電流的控制實現對電機轉矩(電流)、速度、位置的控制。通常是電流作為最內環,速度是中間環,位置作為最外環。
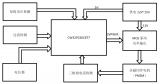
下圖是電流環(最內環)的控制框圖:
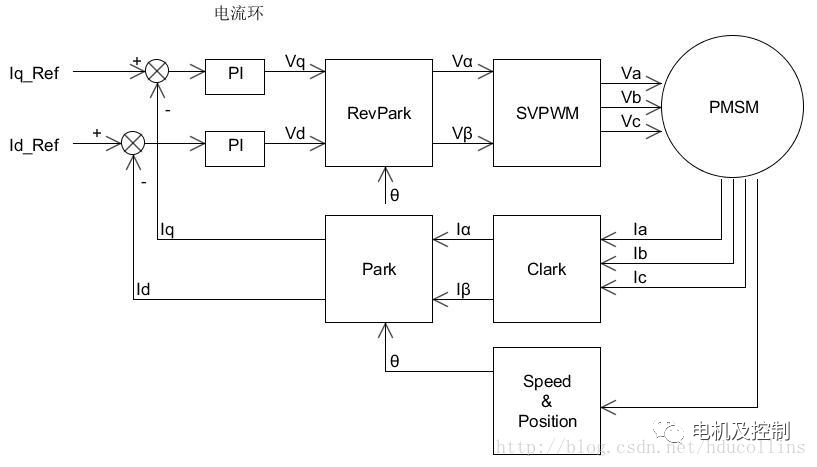
圖一:電流環
在圖一中,Iq_Ref是q軸(交軸)電流設定值,Id_Ref是d軸(直軸)電流設定值,關于交軸直軸不再介紹,大家自行百度。
Ia, Ib, Ic分別是A相、B相、C相的采樣電流,是可以直接通過AD采樣得到的,通常直接采樣其中兩相,利用公式Ia+Ib+Ic=0計算得到第三相,電角度θ可以通過實時讀取磁編碼器的值計算得到。
在得到三相電流和電角度后,即可以進行電流環的執行了:三相電流Ia, Ib, Ic經過Clark變換得到Iα, Iβ;然后經過Park變換得到Iq, Id;然后分別與他們的設定值Iq_Ref, Id_Ref計算誤差值;然后分別將q軸電流誤差值代入q軸電流PI環計算得到Vq,將d軸電流誤差值代入d軸電流PI環計算得到Vd;然后對Vq, Vd進行反Park變換得到Vα, Vβ;然后經過SVPWM算法得到Va, Vb, Vc,最后輸入到電機三相上。這樣就完成了一次電流環的控制。
當對PMSM進行速度控制時,需要在電流環外面加一個速度環,控制框圖如下:
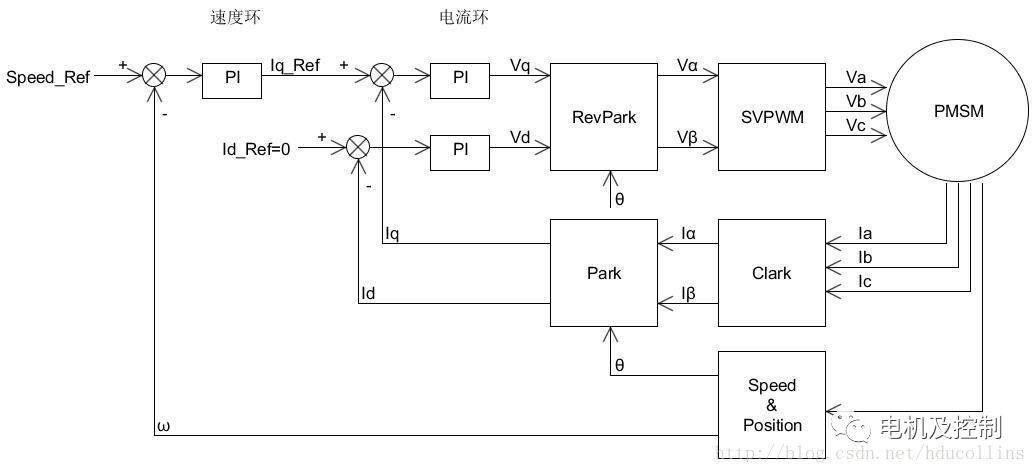
圖二:速度電流雙環
在圖二中,Speed_Ref是速度設定值,ω是電機的轉速反饋,可以通過電機編碼器計算得到。
將計算得到的電機速度ω與速度設定值Speed_Ref進行誤差值計算,代入速度PI環,計算的結果作為電流環的輸入;比較圖二和圖一的電流環部分可以發現,圖二中d軸電流被設定為零(Id_Ref=0),因為d軸電流對于驅動電機的轉動不會產生輸出力,所以通常情況下都會將d軸電流設定為零(但不是總是設定為0的);當Id_Ref=0時,Iq_Ref就等于了速度環的輸出;再結合上面的電流環,就實現了速度電流的雙閉環控制。
當對PMSM進行位置控制時,需要在速度電流環外面加一個位置環,控制框圖如下:
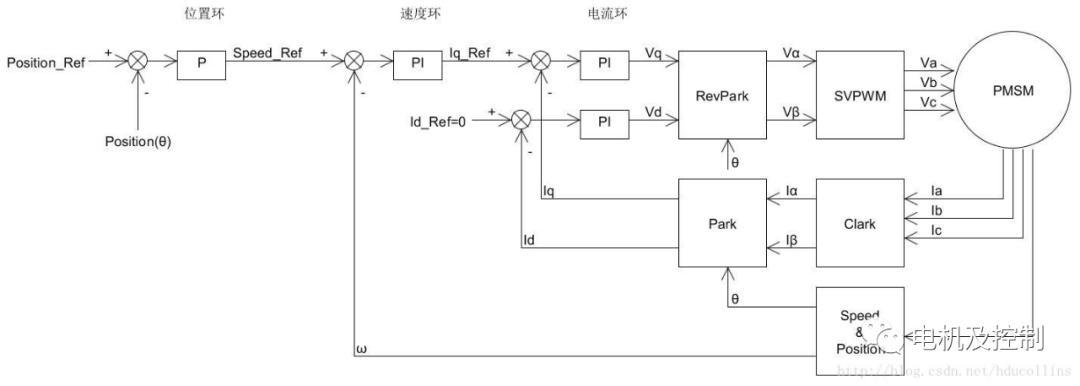
圖三:位置速度電流三環
在圖三中,Position_Ref是位置設定值,Position(θ)是電機的當前位置,可以通過電機編碼器得知,位置控制可以分為電角度位置控制和機械角度位置控制。
將得到的當前位置Position(θ)和位置設定值Position_Ref計算誤差值代入P環,輸出作為速度環的輸入Speed_Ref,在結合上面的速度電流環實現位置速度電流三閉環控制。
在實際使用中,由于磁編碼器無法直接返回電機轉速ω,需要計算一定時間內的磁編碼值變化量來表示電機的轉速ω(M法測速),假設1ms的角度變化量為δ個,則ω=δ/1ms=δ,(單位:個/ms),當電機轉速比較快的時候,這樣的方式是可以的;但是在位置控制的時候,電機的速度會很慢,1分鐘的轉速可能只有1、2轉,用M法測速會存在非常大的誤差,增大單位時間可以適當降低誤差,但隨之而來整個系統的延遲也會增大。
所以為了避免速度環節帶來的誤差以及系統延遲帶來的影響,只使用位置和電流組成的雙環進行控制,不過此時需要對位置環做一定的變化,控制框圖如下:
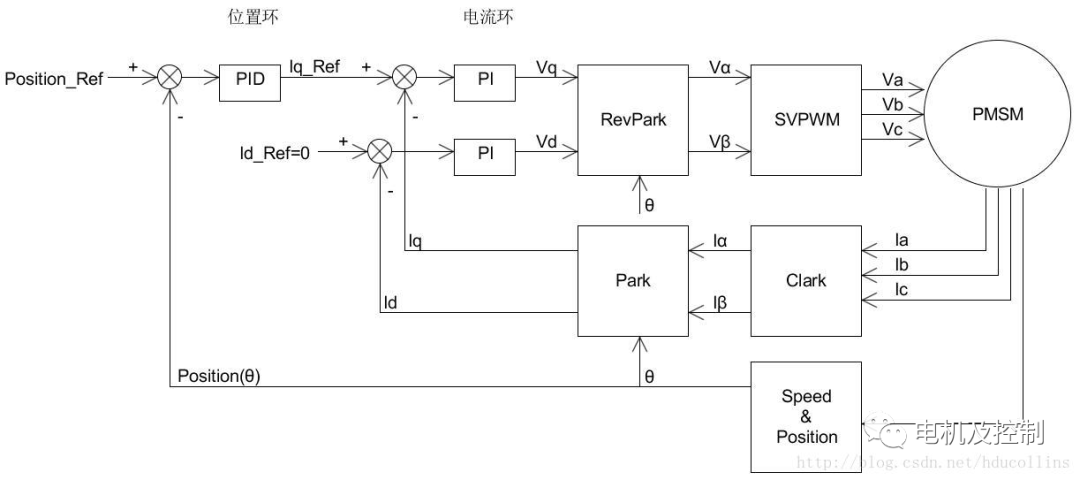
圖四:位置電流雙環
在圖四中,只使用了位置電流雙環實現位置控制。
在位置控制中,會涉及到電機的啟動加速和剎車減速,所以只有P環肯定是不夠的,還需要加入I和D實現PID環進行控制;如果對于位置控制的精度要求不高,允許存在1、2度的誤差的話,可以只使用P和D實現PD環控制即可。
以上簡單介紹了電機控制中的過程,不難發現,主要包括了PID控制器和FOC控制算法。PID控制器是自動控制中最常用的一種控制算法,應用非常廣泛,網上關于PID的資料也非常多,下面詳細講解FOC控制算法。
從上面的控制框圖中可以看出,FOC主要包含了電流采樣、坐標變換(Clark, Park, 反Park)、SVPWM。
前面講過,三相電流Ia, Ib, Ic是可以通過采樣和公式Ia+Ib+Ic=0得到的,并三相電流的相位差是120°,如下圖:
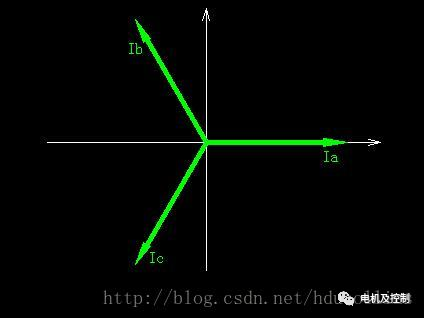
圖五:三相電流
圖五中Ia, Ib, Ic分別是三相電流。
然后經過Clark變換得到Iα, Iβ,如下圖:
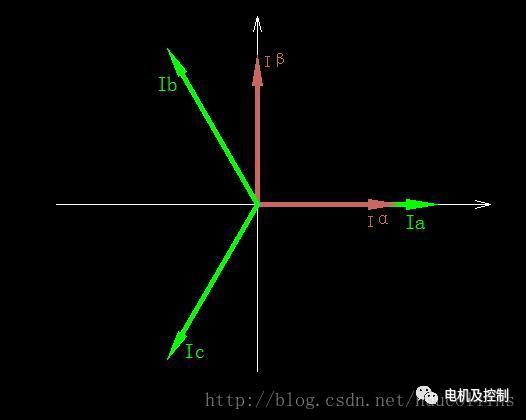
圖六:Clark變換
Clark變換是將靜止的三相a, b, c變換成靜止的兩相α, β,由于不知道如何在編輯器中輸入矩陣,所以選擇在word中寫好截圖過來,公式如下:
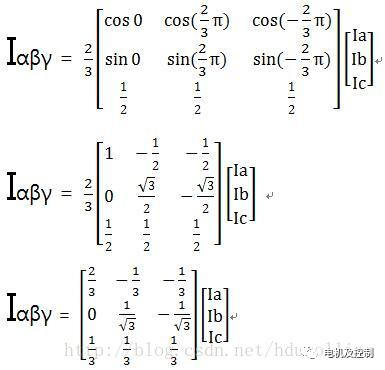
圖六 1
于是可以推導出:
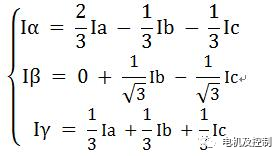
圖六 2
將Ia+Ib+Ic=0代入上面的公式,可以得到:
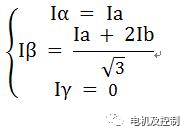
圖六 3
我們需要關心的是Iα和Iβ,所以Clark變化最后的公式就是:
Iα = Ia ;
Iβ = (Ia + 2*Ib) /√3 ;
然后經過Park變換得到Iq, Id,他們是相互垂直的并且同時跟隨著磁場方向在旋轉,如下圖:
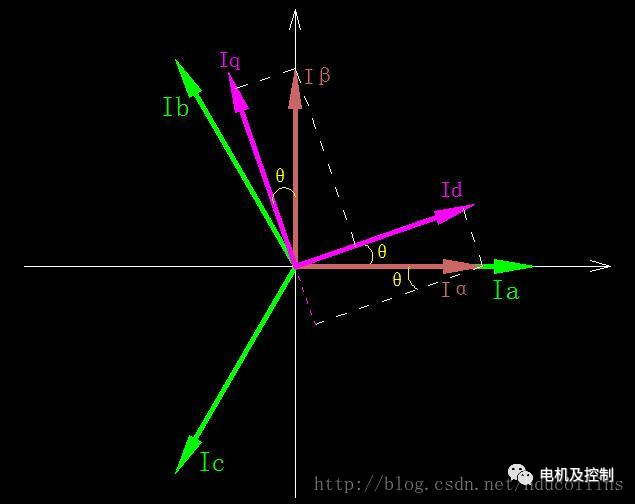
圖七:Park變換
如圖七所示,Park變換是將靜止的α,β電流變換成旋轉的q軸和d軸電流,θ是旋轉的角度,也稱為電角度。
以電角度θ為夾角,分別對Iα,Iβ進行矢量分解,計算投影到q軸和d軸上的電流分量,可以得到以下公式:
Iq = Iβcosθ - Iαsinθ
Id = Iαcosθ + Iβsinθ
在計算得到Iq,Id之后,需要分別跟他們的設定值計算誤差,然后分別做PI控制,得到Vq,Vd。
然后對Vq,Vd進行反Park變換,如下圖:
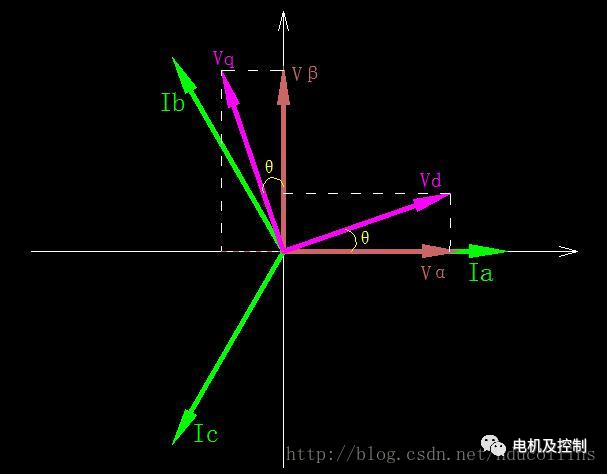
圖八:反Park變換
在圖八中,將Vq,Vd反向變換成Vα,Vβ,變換方式與Park變換類似,以電角度θ為夾角,分別對Vq,Vd進行矢量分解,計算投影到α軸和β軸上的電壓分量,可以得到如下公式:
Vα = Vdcosθ - Vqsinθ;
Vβ = Vqcosθ + Vdsinθ;
在得到Vα和Vβ之后,需要通過SVPWM算法計算Va,Vb,Vc,關于SVPWM算法,網上有篇文章講解的非常好,叫做《SVPWM的原理及法則推導和控制算法詳解》,詳細的內容可以去看這篇文章,下面就根據這篇文章做一些總結性的講解。
SVPWM的全稱是空間矢量脈寬調制(Space Vector Pulse Width Modulation),是由三相功率逆變器的六個功率開關元件組成的特定開關模式產生的脈寬調制波,能夠使輸出電流波形盡可能接近于理想的正弦波形。理論基礎是平均值等效原理,即在一個開關周期內通過對基本電壓矢量加 以組合,使其平均值與給定電壓矢量相等。
假設直流母線電壓為Udc,三相相電壓分別為UA,UB,UC,且相互之間的相位差為120°;假設Um為相電壓有效值,f為電源頻率,則有:
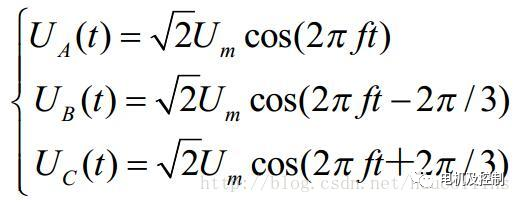
圖八 1
則三相電壓空間矢量相加的合成空間矢量U(t)就可以表示為:
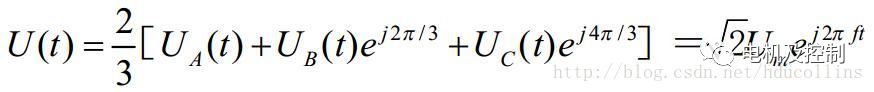
圖八 2
U(t)是一個旋轉的空間矢量,幅值不變,為相電壓峰值,且以角頻率ω=2πf按逆時針方向均勻旋轉,而空間矢量U(t)在三相坐標軸(a,b,c)上的投影就是對稱的三相正弦量。
下面討論一下電壓空間矢量:
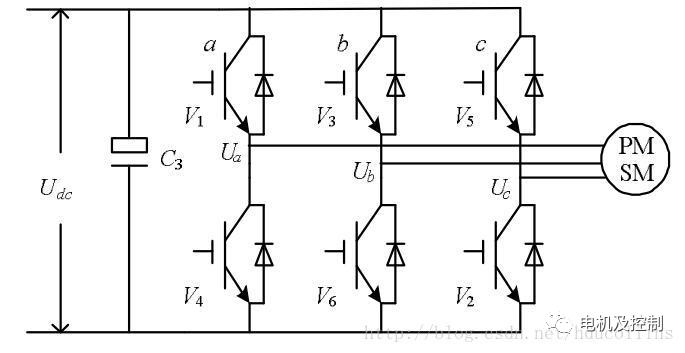
圖九:三相逆變電路
圖九是一個三相逆變電路,每一相在同一時刻只有一個橋會導通,定義這樣一個開關函數Sx(x=a、b、c):
上橋臂導通時,Sx=1;下橋臂導通時,Sx=0。舉個例子:假設a相上橋導通,b和c相下橋導通,那么三相的結果就是a=1,b=0,c=0,組合的結果就是U4(100)。
在同一時刻,如果不同相的上下橋同時存在導通的橋,那么就會有相電流產生,屬于非零矢量;如果同一時刻,三相的上橋同時導通或者三相的下橋同時導通,此時并不會有相電流產生,屬于零矢量。所以總共存在6個非零矢量:U1(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110);以及兩個零矢量:U0(000)、U7(111)。電壓矢量的坐標如下圖所示:
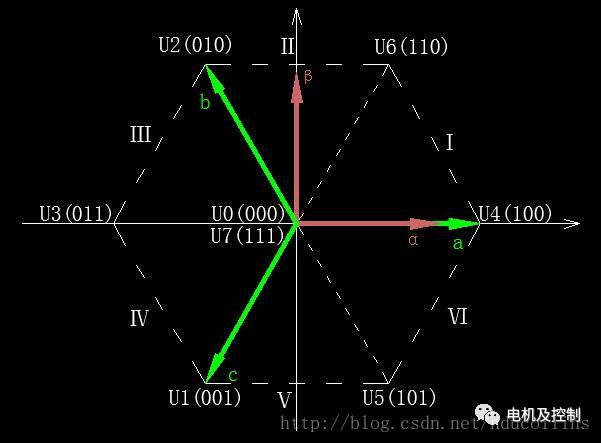
圖十:電壓空間矢量圖
在圖十中,顯示了8個電壓空間矢量U0 ~ U7,以及六個扇區Ⅰ~Ⅵ。
假如Sx(x=a,b,c)=(100),則此時Ua=?Udc,Ub=-?Udc,Uc=-?Udc,同理可以得到其他各種組合下的空間電壓矢量,如下表:
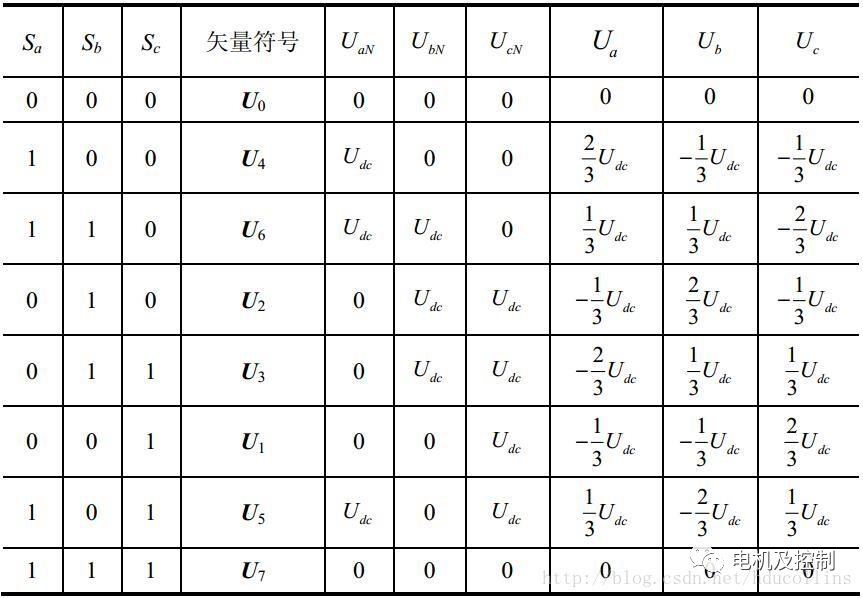
圖十一:電壓空間矢量表
結合圖十和圖十一可知,非零矢量的幅值相同,均為?Udc,相鄰的矢量間隔60°,而兩個零矢量幅值為0,位于中心。在每一個扇區,選擇相鄰兩個電壓矢量以及零矢量,按照伏秒平衡原則來合成每個扇區內的任意電壓矢量,即:
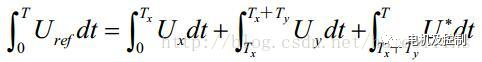
圖十一 1
或者等效成下式:
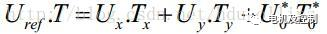
圖十一 2
其中,Uref為期望電壓矢量,T為周期,Tx、Ty、T0分別對應兩個非零矢量Ux、Uy和零矢量U0在一個周期T內的作用時間,其中U0包括U0和U7兩個零矢量。由于最終要得到的是作用在三相半橋上的占空比,也就是三個定時器通道的捕獲比較寄存器的值,所以我們只要能計算出Tx、Ty、T0的值,就可以知道三個捕獲比較寄存器值。
先來看一下當Uref在第Ⅰ個扇區時的情況,見下圖:
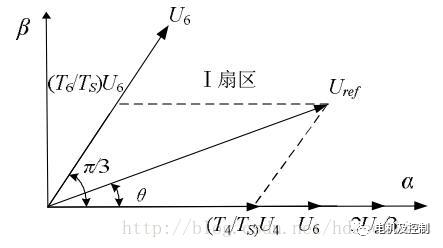
圖十二:電壓空間矢量位于第Ⅰ扇區
如圖十二所示,Uref位于U4和U6之間,由正弦定理可得:

圖十二 1
得到以U4、U6、U7及U0合成的Uref的時間后,接下來就是如何產生實際的脈寬調制波形。在SVPWM調制方案中,零矢量的選擇是最具靈活性的適當選擇零矢量,可最大限度的減少開關次數,盡可能避免在負載電流較大的時刻的開關動作,最大限度的減少開關損耗。因此,我們以減少開關次數為目標,將基本矢量作用順序的分配原則選定為:在每次開關狀態轉換時,只改變其中一相的開關狀態,并且對零矢量在時間上進行了平均分配,以使產生的PWM對稱,從而有效的降低PWM的諧波分量。可以發現當U4(100)切換至U0(000)時,只需改變A相上下一對切換開關,若由U4(100)切換至U7(111)則需要改變B、C相上下兩對切換開關,增加了一杯的切換損失。因此要改變電壓矢量U4(100)、U2(010)、U1(001)的大小,需配合零電壓矢量U0(000),而要改變U6(110)、U3(011)、U5(101),需要配合零電壓矢量U7(111)。這樣通過在不同扇區內安排不同的開關切換順序,就可以獲得對稱的輸出波形,其他各扇區的開關切換順序下表:
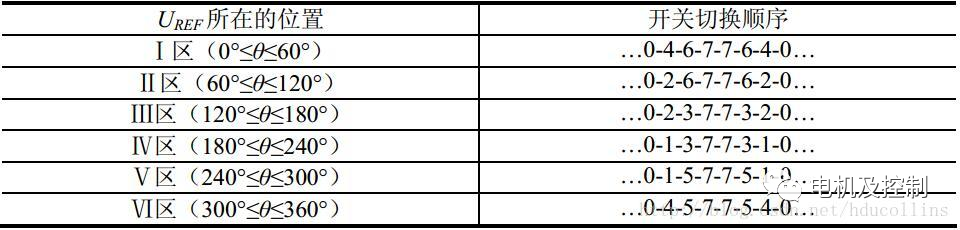
圖十二 2
同樣以第Ⅰ扇區為例,電壓矢量的先后順序為U0、U4、U6、U7、U7、U6、U4、U0,將其畫成a,b,c三相的PWM波形的話就如圖十三所示:
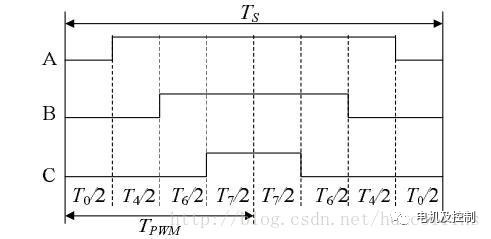
圖十三:第1扇區三相PWM波形
一般我們在控制PMSM的時候都會將PWM波形設定為中央對齊模式,所以在圖十三中,對稱中心的兩邊各個電壓矢量所占的時間都是該電壓矢量在整個周期中所占時間的一半。
要先實現SVPWM的實時調制,我們首先要知道Uref所在的扇區位置,然后才能利用所在扇區的相鄰電壓矢量和適當的零矢量來合成電壓矢量。由圖十二可以知道,電壓矢量Uref與α軸的夾角θ決定了Uref所在的扇區,所以我們只要判斷θ角的大小即可知道Uref所在的扇區。
由 tanθ=Uβ/Uα,可知 θ=arctan(Uβ/Uα),當Uref位于第Ⅰ扇區時,θ滿足0<θ<60°,此時,Uα>0,Uβ>0,tanθ滿足 00,Uβ>0,√3Uα>Uβ。
同理可以得出Uref位于其他扇區時的等價條件,如下:
Uref位于第Ⅱ扇區時的充要條件是:Uβ>0,√3|Uα|
Uref位于第Ⅲ扇區時的充要條件是:Uα<0,Uβ>0,-√3Uα>Uβ;
Uref位于第Ⅳ扇區時的充要條件是:Uα<0,Uβ<0,√3Uα
Uref位于第Ⅴ扇區時的充要條件是:Uβ<0,√3|Uα|<-Uβ;
Uref位于第Ⅵ扇區時的充要條件是:Uα>0,Uβ<0,√3Uα>-Uβ;
進一步分析以上的條件就可以看出,電壓矢量Uref所在的扇區完全由Uβ,√3Uα-Uβ,-√3Uα-Uβ三式決定,
因此令:

圖十三 1
再定義,若U1>0,則A=1,否則A=0;若U2>0,則B=1,否則B=0;若U3>0,則C=1,否則C=0。
再令N=4C+2B+A,則可以通過下標計算Uref所在的扇區。

圖十三 2
接下來就要來計算合成Uref的相鄰電壓矢量的作用時間以及零矢量的作用時間。
假設Uref位于第Ⅰ扇區時(參照圖十二),用到的電壓矢量是U4和U6,所以就需要計算T4和T6,以及零電壓矢量的T0和T7。計算過程如下:
Uα*Ts = |U4|*T4 + |U6|T6cos(π/3);
Uβ*Ts = |U4|T40 + |U6|T6cos(π/6);
前面說過,|U4|=|U6|=?Udc,所以有:
UαTs = ?UdcT4 + ?Udc*T6; ①
UβTs = (UdcT6) / √3; ②
解①,②組成的方程組,得:
T4 = (√3/Udc) * Ts * (√3Uα/2 - Uβ/2) = (√3/Udc) * Ts * U2;
T6 = (√3/Udc) * Ts * Uβ = (√3/Udc) * Ts * U1;
又因為Ts=T0+T4+T6+T7,并且T0和T7的給定是靈活的,可以令T0=T7,那么就有:
T0 = T7 = (Ts - T4 - T6) / 2;
這樣就計算出了Uref位于第Ⅰ扇區時各電壓矢量的時間了。同理可以計算出位于其他扇區時的各電壓矢量時間:
Uref位于第Ⅱ扇區時:
T2 = (-√3/Udc) * Ts * (√3Uα/2 - Uβ/2) = -(√3/Udc) * Ts * U2;
T6 = (-√3/Udc) * Ts * (-√3Uα/2 - Uβ/2) = -(√3/Udc) * Ts * U3;
T0 = T7 = (Ts - T2 - T6) / 2;
Uref位于第Ⅲ扇區時:
T2 = (√3/Udc) * Ts * Uβ = (√3/Udc) * Ts * U1;
T3 = (√3/Udc) * Ts * (-√3Uα/2 - Uβ/2) = (√3/Udc) * Ts * U3;
T0 = T7 = (Ts - T2 - T3) / 2;
Uref位于第Ⅳ扇區時:
T1 =(-√3/Udc) * Ts * Uβ = -(√3/Udc) * Ts * U1;
T3 = (-√3/Udc) * Ts * (√3Uα/2 - Uβ/2) = -(√3/Udc) * Ts * U2;
T0 = T7 = (Ts - T1 - T3) / 2;
Uref位于第Ⅴ扇區時:
T1 = (√3/Udc) * Ts * (-√3Uα/2 - Uβ/2) = (√3/Udc) * Ts * U3;
T5 = (√3/Udc) * Ts * (√3Uα/2 - Uβ/2) = (√3/Udc) * Ts * U2;
T0 = T7 = (Ts - T1 - T5) / 2;
Uref位于第Ⅵ扇區時:
T4 = (-√3/Udc) * Ts * (-√3Uα/2 - Uβ/2) = -(√3/Udc) * Ts * U3;
T5 = (-√3/Udc) * Ts * Uβ = -(√3/Udc) * Ts * U1;
T0 = T7 = (Ts - T4 - T5) / 2;
這樣就完成了Uref位于6個扇區時的各電壓矢量時間的計算,其中√3/Udc是SVPWM調制模式下的最大不失真電壓幅值,在計算定時器各通道的捕獲比較寄存器值時可以將√3/Udc直接去掉;Ts是PWM一個完整周期的時間,也就是定時器的計數周期。
在圖十三中,整個PWM周期中,最先發生的是T0,接下來依次是T4,T6,T7,其中T4,T6是兩個非零矢量,且T4先于T6發生,所以我們可以令先發生的非零矢量時間為Tx,后發生的非零矢量時間為Ty,并且T0=T7,那么就可以得出加載到三個捕獲比較寄存器上的時間分別是:
T1 = (Ts - Tx - Ty) / 4;
T2 = T1 + Tx/2;
T3 = T2 + Ty/2;
只要根據Uref實際所在的扇區,確定Tx和Ty實際所對應的電壓矢量,就可以計算出T1,T2,T3的值;然后再根據Uref所在的扇區畫出類似圖十三的三相PWM波形,就可以確定T1,T2,T3分別對應到三相A,B,C的哪一個通道,再賦值給對應通道的捕獲比較寄存器,就完成了SVPWM算法。
 電子發燒友App
電子發燒友App























評論