永磁同步電機(jī)具有體積小、轉(zhuǎn)動慣量低、結(jié)構(gòu)簡單等優(yōu)點(diǎn)，被廣泛應(yīng)用于控制系統(tǒng)中。然而在實(shí)際應(yīng)用過程中，控制系統(tǒng)會受到高溫、負(fù)載等外界因素的影響，永磁同步電機(jī)的電感、轉(zhuǎn)子磁鏈等參數(shù)會發(fā)生變化，導(dǎo)致系統(tǒng)振蕩，影響實(shí)際控制效果。

因此精確的參數(shù)辨識是為了達(dá)到更好地控制效果的必要條件。目前常用的電機(jī)參數(shù)辨識方法有：卡爾曼濾波算法、最小二乘法、遺傳算法、粒子群算法等。考慮到最小二乘法結(jié)構(gòu)簡單、易于實(shí)現(xiàn)的優(yōu)點(diǎn)，本期采用基于最小二乘法的永磁同步電機(jī)參數(shù)辨識方法。基于對永磁同步電機(jī)的推導(dǎo)，采用定子電壓等可測變量作為輸入輸出，辨識出電機(jī)的定子電阻及d、q軸電樞電感。

1、最小二乘法

最小二乘參數(shù)辨識方法可以解決線性時(shí)變系統(tǒng)、線性定常系統(tǒng)、含有噪聲的線性系統(tǒng)等問題。常見的最小二乘法有：遞推最小二乘法、遺忘因子遞推最小二乘法、修正補(bǔ)償最小二乘法等，這些方法均可以用于系統(tǒng)參數(shù)辨識中。

2、辨識模型的建立

永磁同步電機(jī)是一個非線性的多變量系統(tǒng)。在d、q旋轉(zhuǎn)坐標(biāo)下的電壓方程為：

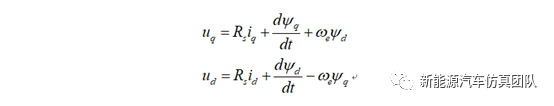
式中，iq和id分別為q、d的電流；uq和ud分別為q、d的電壓；Rs、Lq、Ld分別為定子繞組的電阻和q、d軸的電感；Ψq、Ψd分別為q、d磁鏈的分量；ω為轉(zhuǎn)子的電角速度。

將上述公式修改為最小二乘法的表達(dá)形式：

3、仿真實(shí)驗(yàn)

將S函數(shù)編寫的參數(shù)辨識模塊加入到永磁同步電動機(jī)控制系統(tǒng)模型中進(jìn)行仿真實(shí)驗(yàn)。

function [sys,x0,str,ts] = Synchronous_demarcate2(t,x,u,flag)
%此程序?yàn)楸孀R電機(jī)參數(shù)的轉(zhuǎn)動慣量
switch flag
  case 0  %初始化
    [sys,x0,str,ts]=mdlInitializeSizes;
  case 2 %離散狀態(tài)計(jì)算，下一步仿真時(shí)刻，終止仿真設(shè)定
    sys=[];%mdlUpdates(t,x,u);
  case 3  %輸出信號計(jì)算
    sys=mdlOutputs(t,x,u);
  case {1,4,9}  %輸出信號計(jì)算
    sys=[];
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end


function [sys,x0,str,ts]=mdlInitializeSizes   %系統(tǒng)的初始化
sizes = simsizes;
sizes.NumContStates  = 0;   %設(shè)置系統(tǒng)連續(xù)狀態(tài)的變量
sizes.NumDiscStates  = 0;   %設(shè)置系統(tǒng)離散狀態(tài)的變量
sizes.NumOutputs     = 1;   %設(shè)置系統(tǒng)輸出的變量
sizes.NumInputs      = 3;   %設(shè)置系統(tǒng)輸入的變量
sizes.DirFeedthrough = 1;   %如果在輸出方程中顯含輸入變量u，則應(yīng)該將本參數(shù)設(shè)置為1,輸入不直接傳到輸出口
sizes.NumSampleTimes = 1;   % 模塊采樣周期的個數(shù)
                            % 需要的樣本時(shí)間，一般為1.
                            % 猜測為如果為n，則下一時(shí)刻的狀態(tài)需要知道前n個狀態(tài)的系統(tǒng)狀態(tài)
sys = simsizes(sizes);
x0  = [];            % 系統(tǒng)初始狀態(tài)變量
str = [];                   % 保留變量，保持為空
ts  = [-1 0];                   % 采樣時(shí)間[t1 t2] t1為采樣周期，如果取t1=-1則將繼承輸入信號的采樣周期；參數(shù)t2為偏移量，一般取為0


global  P_past2 theta_past2 
P_past2 = 1e4 * eye(2,2);  %一般取1e4 - 1e10
theta_past2 = [0.0001; 0.0001];       %一般取一個極小的正實(shí)向量


function sys=mdlOutputs(t,x,u)   %產(chǎn)生（傳遞）系統(tǒng)輸出
%初值的確定
lambda = 0.99;  %遺忘因子0-1
global   P_past2 theta_past2
xt = [u(1) u(2)];  %1*2 fait
y = u(3);
I = [1 0;0 1];


K = P_past2*xt'/(lambda + xt * P_past2*xt');   %2*1
P_new = 1/lambda*(I - K*xt) * P_past2;  %2*2
theta_new = theta_past2 + K*(y-xt*theta_past2);   %2*1


P_past2 = P_new ;
theta_past2 = theta_new;


sys(1) = theta_new(1);

function [sys,x0,str,ts] = Synchronous_demarcate(t,x,u,flag)
%此程序?yàn)楸孀R電機(jī)參數(shù)的定子電阻Rs, 永磁體磁通faif, dq軸電感L
switch flag
  case 0  %初始化
    [sys,x0,str,ts]=mdlInitializeSizes;
  case 2 %離散狀態(tài)計(jì)算，下一步仿真時(shí)刻，終止仿真設(shè)定
    sys=[];%mdlUpdates(t,x,u);
  case 3  %輸出信號計(jì)算
    sys=mdlOutputs(t,x,u);
  case {1,4,9}  %輸出信號計(jì)算
    sys=[];
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end


function [sys,x0,str,ts]=mdlInitializeSizes   %系統(tǒng)的初始化
sizes = simsizes;
sizes.NumContStates  = 0;   %設(shè)置系統(tǒng)連續(xù)狀態(tài)的變量
sizes.NumDiscStates  = 0;   %設(shè)置系統(tǒng)離散狀態(tài)的變量
sizes.NumOutputs     = 3;   %設(shè)置系統(tǒng)輸出的變量
sizes.NumInputs      = 5;   %設(shè)置系統(tǒng)輸入的變量
sizes.DirFeedthrough = 1;   %如果在輸出方程中顯含輸入變量u，則應(yīng)該將本參數(shù)設(shè)置為1,輸入不直接傳到輸出口
sizes.NumSampleTimes = 1;   % 模塊采樣周期的個數(shù)
                            % 需要的樣本時(shí)間，一般為1.
                            % 猜測為如果為n，則下一時(shí)刻的狀態(tài)需要知道前n個狀態(tài)的系統(tǒng)狀態(tài)
sys = simsizes(sizes);
x0  = [];            % 系統(tǒng)初始狀態(tài)變量
str = [];                   % 保留變量，保持為空
ts  = [0 0];                   % 采樣時(shí)間[t1 t2] t1為采樣周期，如果取t1=-1則將繼承輸入信號的采樣周期；參數(shù)t2為偏移量，一般取為0


global  P_past theta_past
P_past = 1e4 * eye(3,3);
theta_past = [0;0;10000];


function sys=mdlOutputs(t,x,u)   %產(chǎn)生（傳遞）系統(tǒng)輸出
%初值的確定
lambda = 1;  %遺忘因子， 選擇不遺忘 0.8~1
global   P_past theta_past
id = u(1);
iq = u(2);
w = u(3);    %電角速度 = 轉(zhuǎn)子速度 * 極對數(shù)
diq = u(4);
uq = u(5);
xt = [-iq -w uq];
y = diq+w*id;
P_new = 1/lambda*(P_past-(P_past*(xt'*xt)*P_past)/(lambda+xt*P_past*xt'));
L = P_past*xt'/(lambda+xt*P_past*xt');
theta_new = theta_past + L*(y-xt*theta_past);
a = theta_new(1);
b = theta_new(2);
c = theta_new(3);
R = a/c;
Ke = b/c;
Ld = 1/c;
P_past = P_new ;
theta_past = theta_new;
sys(1) = R;
sys(2) = Ke;
sys(3) = Ld;

轉(zhuǎn)動慣量參數(shù)辨識結(jié)果：

電磁電感參數(shù)辨識結(jié)果：

電角速度觀測值：

負(fù)載觀測結(jié)果：

三相電流觀測結(jié)果：

仿真結(jié)果表明，采用遞推最小二乘法的參數(shù)辨識算法能夠準(zhǔn)確辨識出電機(jī)的電磁參數(shù)，能夠很好地跟隨電機(jī)參數(shù)的變化，具有快速的收斂性和良好的辨識結(jié)果。