一、什么是進位計數制
數制也稱計數制,是指用一組固定的符號和統一的規則來表示數值的方法。按進位的原
則進行計數的方法,稱為進位計數制。比如,在十進位計數制中,是按照“逢十進一”的原則進行計數的。
常用進位計數制:
1、十進制(Decimalnotation),有10個基數:0~~9,逢十進一;
2、二進制(Binarynotation),有2個基數:0~~1,逢二進一;
3、八進制(Octalnotation),有8個基數:0~~7,逢八進一;
4、十六進制數(Hexdecimalnotation),有16個基數:0~~9,A,B,C,D,E,F
(A=10,B=11,C=12,D=13,E=14,F=15),逢十六進一。
二、進位計數制的基數與位權
基數和位權是進位計數制的兩個要素。
1、基數:
所謂基數,就是進位計數制的每位數上可能有的數碼的個數。例如,十進制數每位上的數碼,
有0、1、3,…,9十個數碼,所以基數為10。
2、位權:
所謂位權,是指一個數值的每一位上的數字的權值的大小。例如十進制數4567從低位到高
位的位權分別為100、101、102、103。因為:
4567=4x103+5x102+6x101+7x100
3、數的位權表示:
任何一種數制的數都可以表示成按位權展開的多項式之和。
比如:十進制數的435.05可表示為:
435.05=4x102+3x101+5x100+0x10-1+5x10-2
位權表示法的特點是:每一項=某位上的數字X基數的若干冪次;而冪次的大小由該數字所
在的位置決定。
三、二進制數
計算機中為何采用二進制:二進制運算簡單、電路簡單可靠、邏輯性強。
1、定義:
按“逢二進一”的原則進行計數,稱為二進制數,即每位上計滿2時向高位進一。
2、特點:
每個數的數位上只能是0,1兩個數字;二進制數中最大數字是1,最小數字是0;基數為
2;
比如:10011010與00101011是兩個二進制數。
3、二進制數的位權表示:
(1101.101)2=1x23+1x22+0x21+1x20+1x2-1+0x2-2+1x2-3
4、二進制數的運算規則:
加法運算
①0+0=0③1+1=10
②0+1=1+0=1
乘法運算
①0×0=0③1×1=1
②0×1=1×0=0
四、八進制數
1、定義:
按“逢八進一”的原則進行計數,稱為八進制數,即每位上計滿8時向高位進一。
2、特點:
每個數的數位上只能是0、1、2、3、4、5、6、7八個數字;八進制數中最大數字是7,最
小數字是0;基數為8;
比如:(1347)8與(62435)8是兩個八進制數。
3、八進制數的位權表示:
(107.13)8=1x82+0x81+7x80+1x8-1+3x8-2
五、十六進制數
1、定義:
按“逢十六進一”的原則進行計數,稱為十六進制數,即每位上計滿16時向高位進一。
2、特點:
每個數的數位上只能是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六個數碼;
十六進制數中最大數字是F,即15,最小數字是0;基數為16;
比如:(109)16與(2FDE)16是兩個十六進制數。
3、十六進制數的位權表示:
(109.13)16=1x162+0x161+9x160+1x16-1+3x16-2
(2FDE)16=2x163+15x162+13x161+14x160
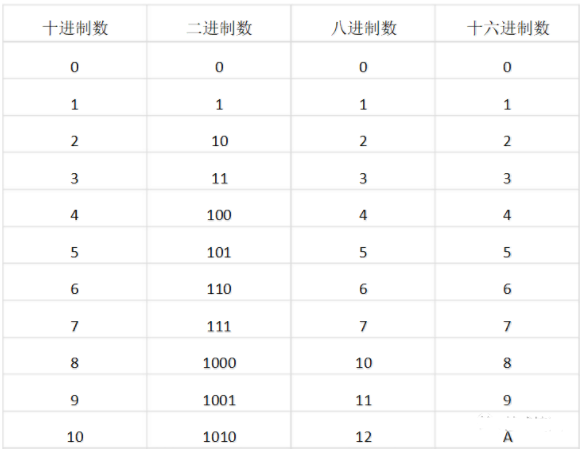
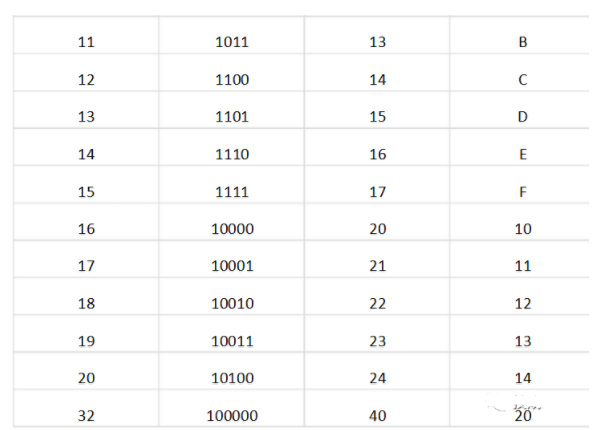
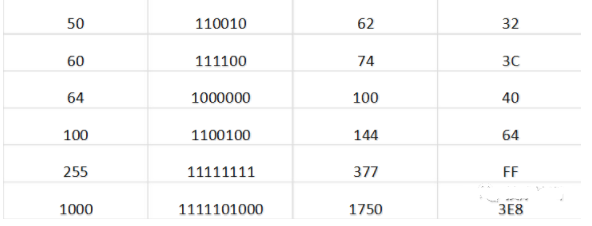
六、常用計數制間的對應關系
二進制數、八進制數、十六進制數及十進制數是現代數字系統中常用的四種數制,這幾種進位制計數制之間的對應關系如表1所列。
表1常用計數制數的表示方法
七、數制間的轉換
1、十進制數轉換成非十進制數
(1)十進制整數轉換成非十進制整數
①為什么要進行數制間的轉換?
將數由一種數制轉換成另一種數制稱為數制間的轉換。
因為日常生活中經常使用的是十進制數,而在計算機中采用的是二進制數。所以在使用計算
機時就必須把輸入的十進制數換算成計算機所能夠接受的二進制數。計算機在運行結束后,
再把二進制數換算成人們所習慣的十進制數輸出。這兩個換算過程完全由計算機自動完成。
②轉換方法
十進制整數化為非十進制整數采用“余數法”,即除基數取余數。
把十進制整數逐次用任意十制數的基數去除,一直到商是0為止,然后將所得到的余數由
下而上排列即可。
②十進制小數轉換成非十進制小數轉換方法
十進制小數轉換成非十進制小數采用“進位法”,即乘基數取整數。
把十進制小數不斷的用其它進制的基數去乘,直到小數的當前值等于0或滿足所要求的精度
為止,最后所得到的積的整數部分由上而下排列即為所求。
2、非十進制數轉換成十進制數
非十進制數轉換成十制數采用“位權法”,即把各非十進制數按位權展開,然后求和。
3、二、八、十進制數之間轉換
(1)二進制數與八進制數之間的轉換轉換方法
①把二進制數轉換為八進制數時,按“三位并一位”的方法進行。
以小數點為界,將整數部分從右向左每三位一組,最高位不足三位時,添0補足三位;小數
部分從左向右,每三位一組,最低有效位不足三位時,添0補足三位。然后,將各組的三位
二進制數按權展開后相加,得到一位八進制數。
②將八進制數轉換成二進數時,采用“一位拆三位”的方法進行。
即把八進制數每位上的數用相應的三位二進制數表示。
③二進制數與十六進制數之間的轉換轉換方法
a、把二進制數轉換為十六進制數時,按“四位并一位”的方法進行。
以小數點為界,將整數部分從右向左每四位一組,最高位不足四位時,添0補足四位;小數
部分從左向右,每四位一組最低有效位不足四位時,添0補足四位。然后,將各組的四位二
進制數按權展開后相加,得到一位十六進制數。
b、將十六進制數轉換成二進數時,采用“一位拆四位”的方法進行。
即把十六進制數每位上的數用相應的四位二進制數表示。
編輯:黃飛
?
 電子發燒友App
電子發燒友App










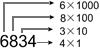







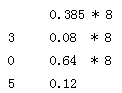















評論